Матрица плотности чистого состояния

При рассмотрении чистого состояния 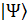матрица плотности будет определяться проектором:

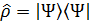(2.2)

Матрица плотности определена матричными элементами оператора 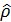в произвольном ортонормированном базисе :

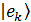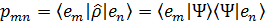(2.3)

Разложим вектор 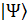по базису: 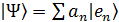, тогда для среднего значения A получим:

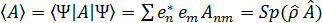(2.4)

Из уравнения Шредингера получим уравнение динамической эволюции для оператора :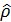

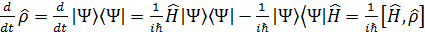(2.5)

При рассмотрении чистого состояния использование матрицы плотности удобнее чем использование вектора состояния, так как глобальная фаза вектора состояния системы в матрице плотности исключена. На феноменологическом уровне можно ввести понятие время релаксации и декогеренции.

Матрица плотности смешанного состояния

Оператор плотности описывает смешанное состояние:

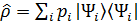, (2.6)

Или же в произвольном базисе, который является ортонормированным, 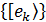матрицей плотности с элементами:

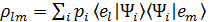(2.6)

При рассмотрении частного случая чистого состояния кроме одного значения вероятности равного единице, остальные будут равны нулю. Опишем физический смысл матрицы плотности. В базисе 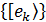имеем:

,

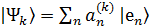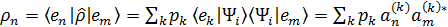. (2.7)

Диагональный элемент 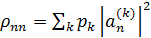матрицы плотности будет равен вероятности состояния 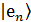в k-той компоненте статистического ансамбля. Получим что диагональные элементы матрицы плотности показывают вероятность нахождения системы в состояния 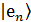, что называется заселенностью соответствующего состояния. Когерентностями называют недиагональные компоненты. В состоянии теплового равновесия когерентности будут равны нулю, а заселенность будет экспоненциально убывать при увеличении температуры.

Матрица плотности кубита

При учете, что: 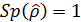, матрица плотности кубита будет иметь вид:

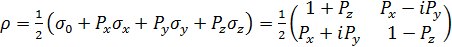. (2.8)

Вектор 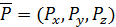показывает координаты точки внутри сферы Блоха, которые соответствуют состоянию кубита 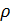. Все точки, представляющие смешанные состояния лежат внутри сферы Блоха. Например, 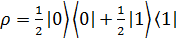полностью смешанное состояние, находится в точке центра сферы Блоха.

Глава 2. Сверхпроводящие кубиты

Свойства сверхпроводников

Одним из наиболее ярких открытий 20 века стала сверхпроводимость. Камерлинг Оннес в 1911 обнаружил данное свойство. Главным параметров сверхпроводников является критическая температура 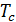, если показание температуры будет ниже данного показателя, то его сопротивление становится равным нулю. Показатель критической температуры очень низок, из-за этого многие физики поставили перед собой задачу о повышении показателя критической температуры.

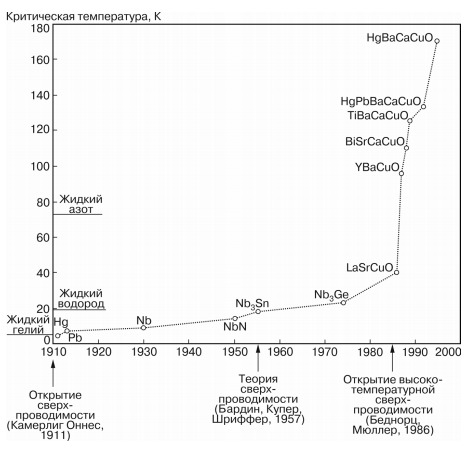
Рис. 3. Хронология повышения температуры сверхпроводящего провода.

В 1986 году произошел настоящий скачек Дж. Борнорец и К. Мюллер открыли сверхпроводимость при высоких температурах, которая превысила температуру кипения жидкого азота (-196 ⁰C).

Рассмотрим фундаментальные свойства сверхпроводников, установленные теоретически и подтверждённые на опыте.

Бесконечная проводимость

Проводимость сверхпроводника будет стремиться к бесконечности, так как сопротивление будет равно нулю. При температуре 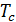и с понижением температуры происходит переход в сверхпроводящее состояние. Если рассмотреть ток, протекающий через сверхпроводник, то мы увидим, что он будет являться бездиссипативным. Тогда исходя из закона Джоуля-Ленца

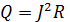, мы можем сделать вывод, что мощность будет равна нулю.

Идеальный дагмагнетизм

Бесконечная проводимость не могла объяснить особое поведение сверхпроводника в магнитном поле. Вальтер Мейсснер и Роберт Оксенфельд выяснили что магнитное поле не проходит сквозь толщу сверхпроводника. По всей области сверхпроводника, кроме области близкой к поверхности, магнитная индукция равна нулю.

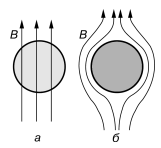
Рис. 4. Эффект Вальтера Мейсснера. Магнитное поле выталкивается из сверхпроводника. (а)-нормальный металл, (б)-сверхпроводник

Энергетическая щель

По сравнению с термодинамическими свойствами металлов, термодинамические свойства сверхпроводников так же отличаются. В спектре квазичастичных электронных возбуждений есть запрещенный интервал энергии, так же называемый щелью Δ. Значение температуры существенно влияет на величину щели.

Квантование магнитного потока

Рассмотрим массивное кольцо, состоящее из сверхпроводника. В таком кольце циркулирующий ток, а также создаваемое им магнитное поле не могут принимать произвольные значения. Другими словами, в отверстии поток магнитного поля Φ принимает лишь дискретные значения:

.

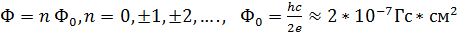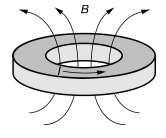
Рис. 5. Магнитное поле, создаваемое циркулирующим током в сверхпроводящем кольце.

Квазистатичные возбуждения

Вследствии уменьшения температуры сверхпроводника процессы диссипации и декогерентности существенно подавляются. Для обеспечения в сверхпроводниках низкого уровня процессов диссипации и декогерентности нужно чтобы выполнялись условия: 1) 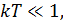2) .

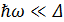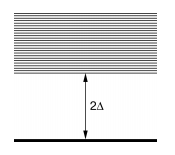
Рис. 6. Квазичастичные возбуждения в сверхпроводнике.

Эффект Брайана Джозефсона

Сверхпроводящие структуры, содержащие джозефсонские контакты, являются основой для джозефсоноских контактов. Такие контакты состоят из двух сверхпроводников, разделенных тонким слоем диэлектрика.

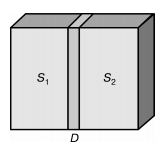
Рис.7 Джозефсонский контакт.

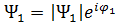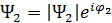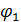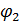Сверхпроводник S₁ характеризуется волновой функцией , а сверхпроводник S₂ характеризуется функцией . Если между берегами не будет взаимодействия, то это приведет к отсутствию корреляции меду фазами, но при этом фазы и когерентны в каждом из проводников. Обмен электронами приводит к фазовой когерентности в системе и установлению разности фаз 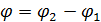на контакте. Открытие состоит в том, что сверхпроводящий ток может протекать без сопротивления через туннельный барьер диэлектрика, а значение будет связано с разностью фаз 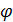[38].

Джозефсон определил два эффекта:

Стационарный Джозефсонский эффект

Первым соотношением Джозефсона определяется зависимость сверхпроводящего тока, проходящего через туннельный барьер, от разности фаз на контакте:

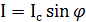. (3.1)

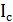- это критический ток, показывающее максимальное значение бездиссипативного тока, проходящего через контакт. При повышении критического тока появляется диссипативная компонента тока квазичастиц, тем самым вызывая возникновение напряжения .

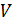Нестационарный Джозефсонский эффект

Связь напряжения на контакте с производной фазы по времени описывает второе соотношение Джозефсона:

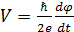. (3.2)

Если к джозефскому контакту приложить постоянный ток, что приложенный ток, согласно соотношениям Джозефсона, будет ассоциировать с частотой:

(3.3)

Постоянное напряжение на концах контактов двух сверхпроводников вызывает переменный ассоциирующий ток.

Эффект Джозефсона наблюдается даже при слабой связи между сверхпроводниками. Разные типы сверхпроводящих контактов (микро-мостики, точечные контакты) обладают различными ток-фазовыми зависимостями 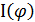, которые обладают 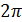- периодичностью, но неявляются синусоидальными.

Сверхпроводящие кубиты

Сверхпроводящие кубиты реализуются путем использования методов «теневого напыления» и электронно-лучевой литографии. Сверхпроводящие кубиты состоят из сверхпроводниковых петель, размеры которых сравнимы с микронными размерами, в эти петли вживляются джозефсоновские переходы. Джозефсоновские переходы обладают нелинейной индуктивностью и емкостью. Как было сказано в предыдущем разделе, где был описан эффект Джозефсона [38], при «разрыве» сверхпроводника слабой связью, по сверхпроводнику начинает течь ток 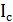, который зависит от разности фаз 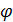сверхпроводящих электронов. Если сравнить эффективный гамильтониан системы, описывающей переход, с гамильтонианом нелинейного маятника, то можно заметить, что они схожи, притом угол отклонения маятника от состояния покоя играет роль разности фаз на берегах контакта. Но чтобы использовать систему с джозевсоновскими переходами в качестве логического элемента, нужно чтобы выполнялись определенные условия:

1. Эффект шумов.

Цепь должна полностью состоять из сверхпроводников, так же должны использоваться сверхнизкие температуры для так называемого «замораживания» квазичастотных возбуждений. То есть энергия тепловых флуктуаций должна быть много меньше чем расстояние между самыми нижними уровнями энергитического спектра 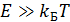,где 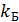- постоянная Больцмана. То есть температура должна придерживаться в районе нескольки мК.

2. Отделение двух уровней от основного энергетического спектра

Если создать нелинейную индуктивность контакта, то это условие будет выполняться.

Чтобы описать квантовые свойства джозефсоноских систем, нужно применить методику канонически сопряженных переменных. Получаем следующий коммутатор 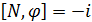. То есть параметры N- число куперовских пар и 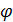- разность фаз не могут быть одновременно определены, они испытывают квантовые флуктуации. Если провести аналогию, то мы можем прийти к следующему выражению 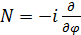. Тогда мы можем записать гамильтониан нелинейного осциллятора, в случае обособленного джозефсоновского контакта с током :

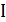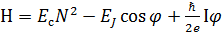, (4.1)

где 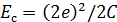-кулоновская энергия, необходимая для сдерживания куперовских пар при заряде 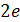и 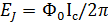-джозефсоновская энергия, приходящаяся на связь кванта потока 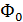в нелинейной индуктивности

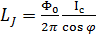, что является самой мерой силы связи джозефсоновского перехода. Можно сделать вывод что из-за квантового туннелирования через потенциальный барьер удержание частицы в потенциальной яме невозможно [38]. Однако, при условии, что полная энергия будет много меньше энергии джозефсона 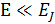вероятность такого туннелирования становится очень малой, так же частота перехода между уровнями кубита имеет большую зависимость от соотношения между кулоновской и джозефсоновской энергиями [38].

В зависимости от соотношения между кулоновской энергией и джозефсоновской энергией сверхпроводящие кубиты можно подразделить на три группы: зарядовый, потоковый и фазовый кубиты. Соотношения между энергиями можно менять разными способами, например, меняя размер джозефсоновского перехода, что вносит вклад и в емкость, тем самым меняя энергию. Каждый из трех реализованных типов имеет свои преимущества, а также и недостатки.

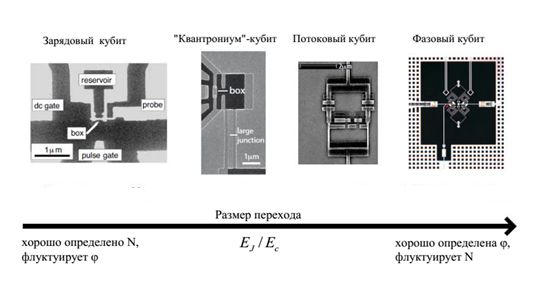
Рис.8 Изображения со сканирующего электронного микроскопа различных типов сверхпроводящих кубитов. Отношение 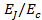возрастает с увеличением размеров перехода, что, в свою очередь, определяет, какая из двух канонически сопряженных величин, j или N