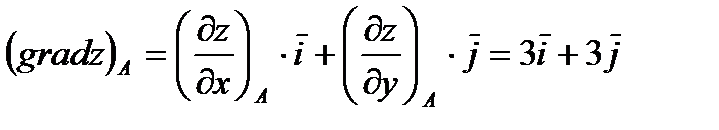Функции двух переменных. Предел. Непрерывность.

Частные производные.

Задача 1.Найти частные производные от функций:

а) .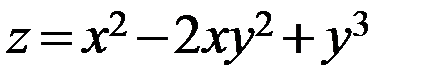

Решение. Частную производную 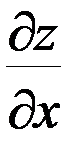находим как производную функции 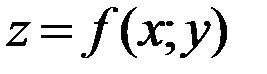по аргументу 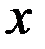в предположении, что 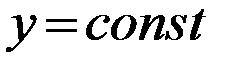. Поэтому,

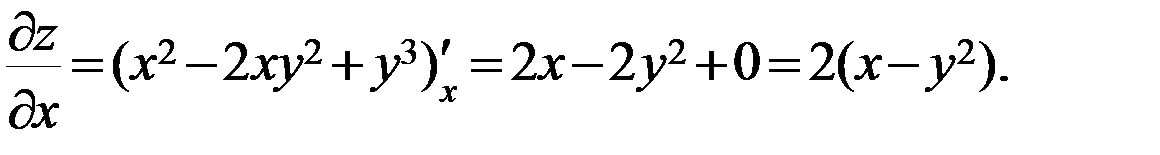
Аналогично,

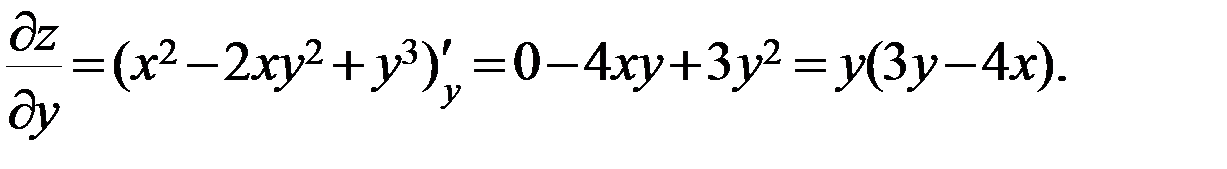
б)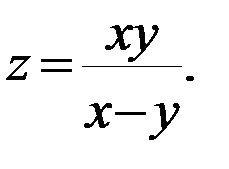

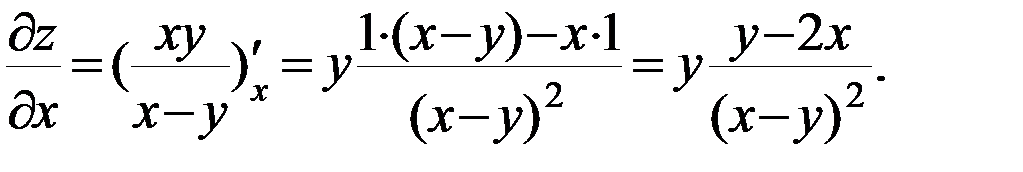
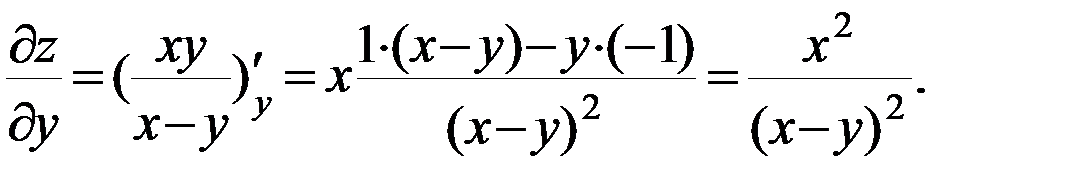
в)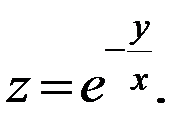

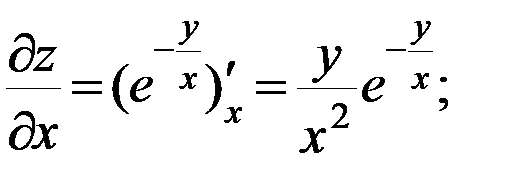
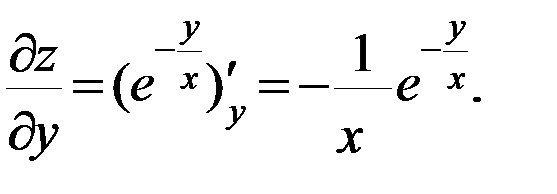
г)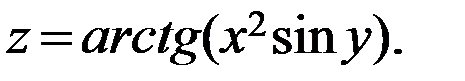

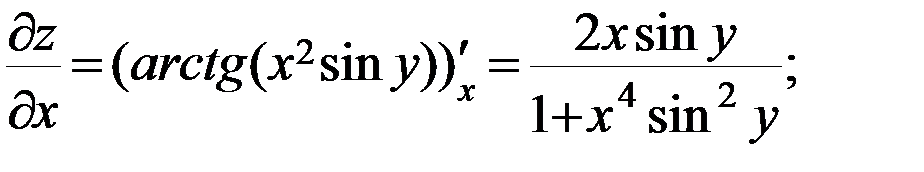
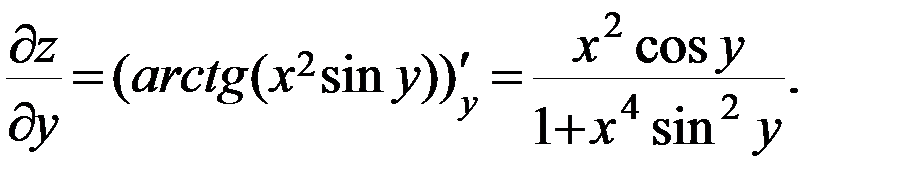
Пример 2

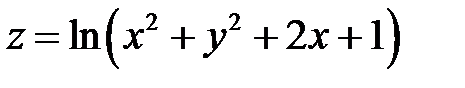. Показать, что .

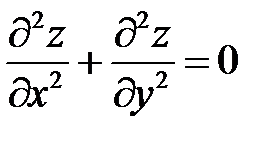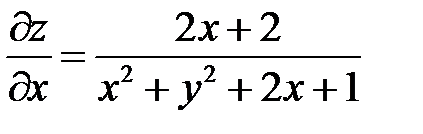
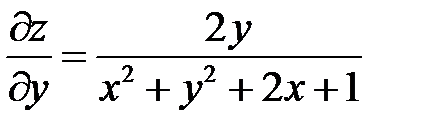
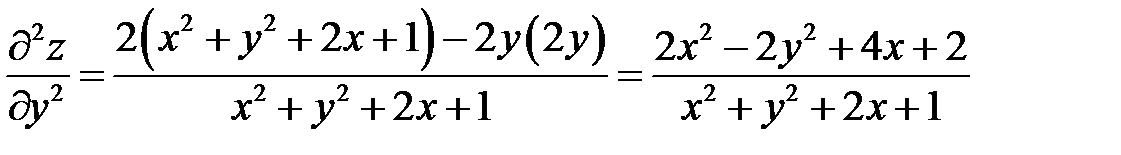
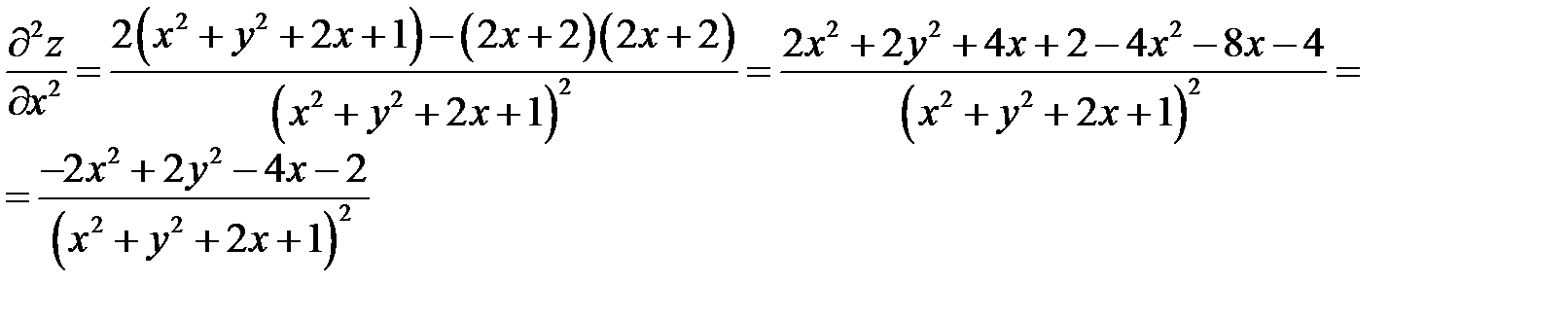
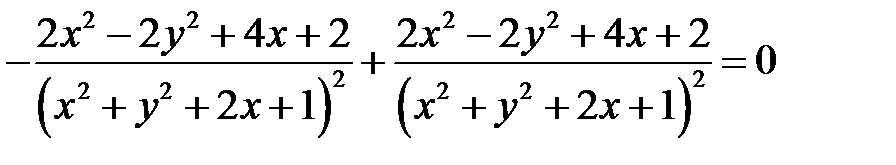
Пример 3

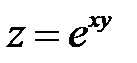. Показать, что .

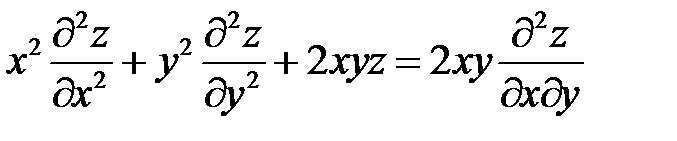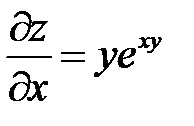
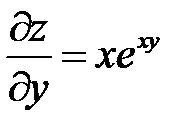
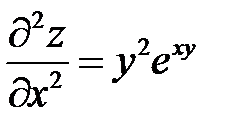
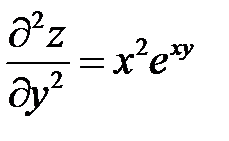
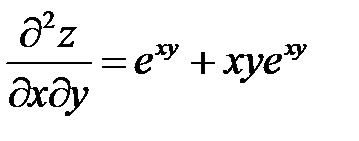
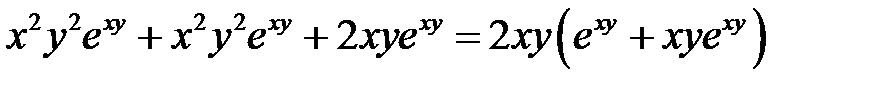
Производная сложной функции. Производная неявной функции

Задача 1.Продифференцировать сложную функцию:

а)

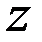Решение. Так как и зависят от переменных и , то функция в конечном итоге зависит от переменных и , и ее частные производные можно найти по формулам:

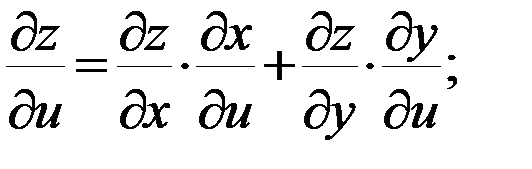
Следовательно,

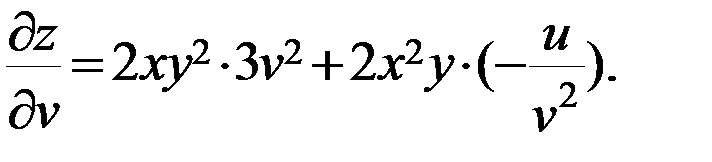
б) Найти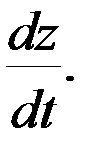

Решение. Так как функция 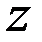в конечном итоге зависит от одной переменной , то ее производную можно найти по формуле:

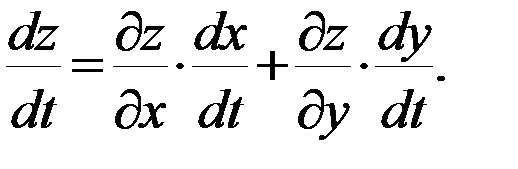Тогда,

Экстремум функции

Дана функция .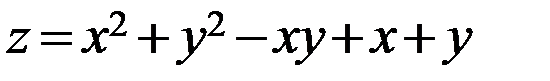

а) исследовать функцию на экстремум;

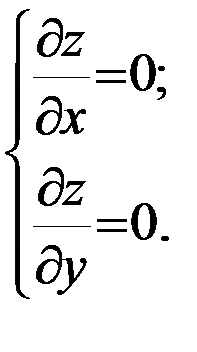
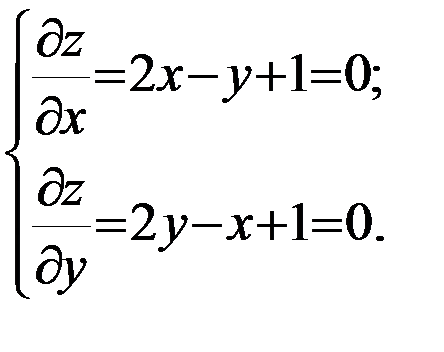
Решение. а) Найдем стационарные точки функции из системы уравнений: 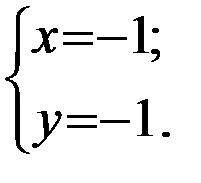Следовательно,

Точка 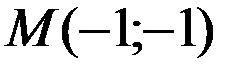- стационарная точка функции. Вычислим значения частных производных второго порядка в точке .

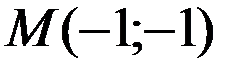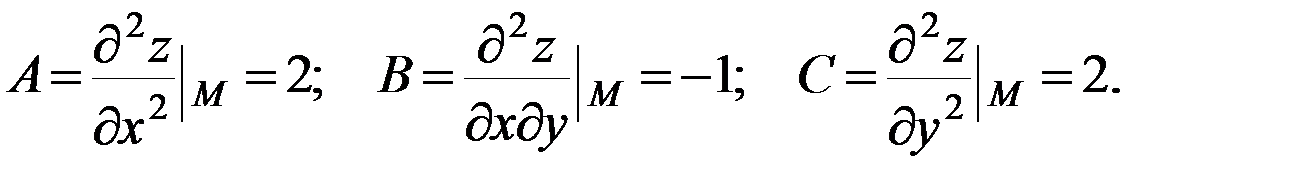
Составим дискриминант 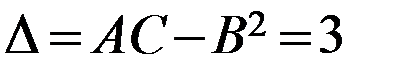. Так как 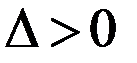, то экстремум есть, так как 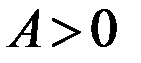, то 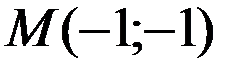- точка минимума.

Наименьшее и наибольшее значение функции в замкнутой области

Задание 1 Дана функция .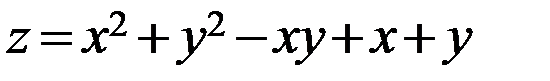

найти наибольшее и наименьшее значения функции в замкнутой области 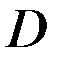, заданной системой неравенств , сделать чертеж области.

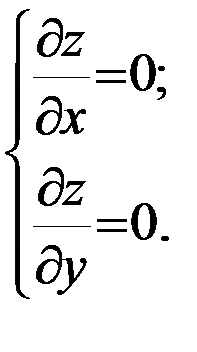
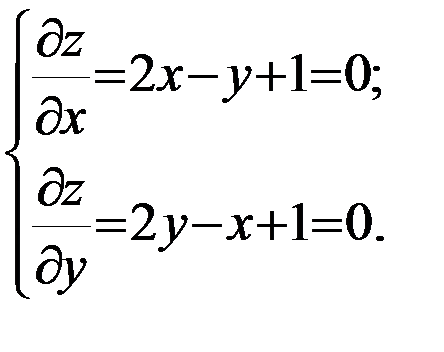
Решение. а) Найдем стационарные точки функции из системы уравнений: 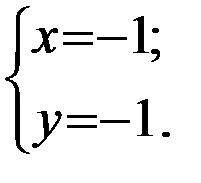Следовательно,

Точка 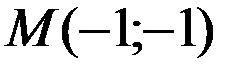- стационарная точка функции. Вычислим значения частных производных второго порядка в точке .

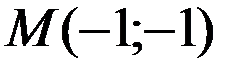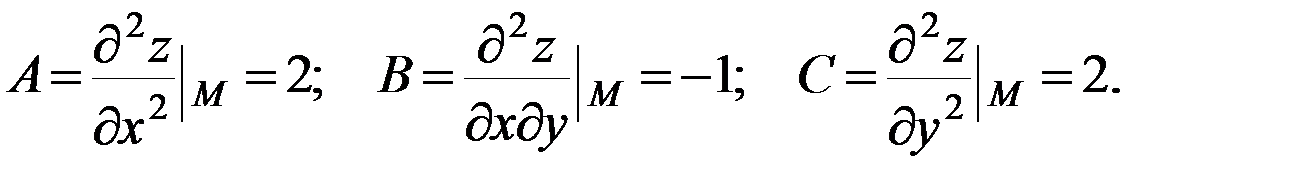
Составим дискриминант 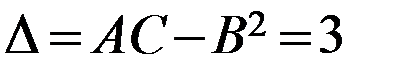. Так как 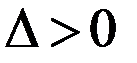, то экстремум есть, так как 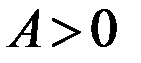, то 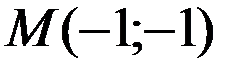- точка минимума.

б) Построим область 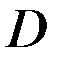, заданную системой неравенств .

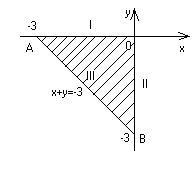
Это треугольник с вершинами в точках О(0;0), А(-3;0), В(0;-3).

Наибольшее и наименьшее значения в замкнутой области 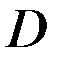функция может достигать в стационарных точках, принадлежащих области 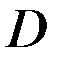и на границе области. Поэтому:

Вычислим значение функции в стационарной точке 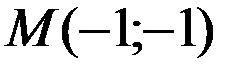, принадлежащей области : .

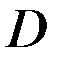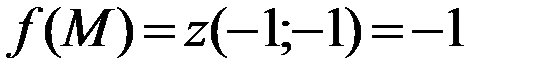Вычислим значения функции в точках О(0;0), А(-3;0), В(0;-3), которые являются точками «стыковки» различных участков границы области.

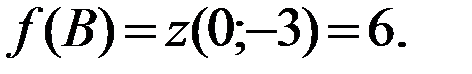
Вычислим значения функции в критических точках на границе области.

I участок: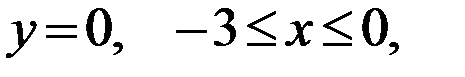

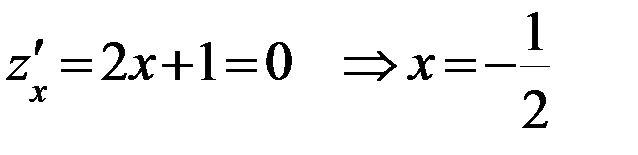- критическая точка, принадлежащая [-3;0].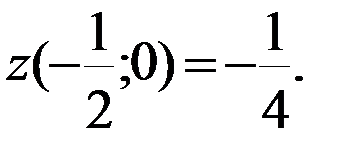

II участок: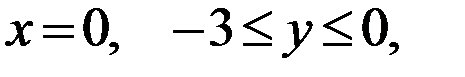

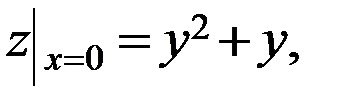
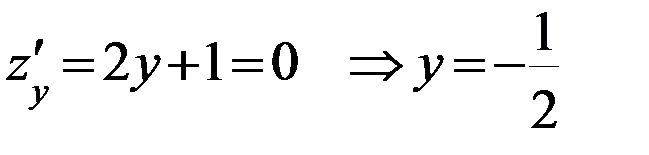- критическая точка, принадлежащая [-3;0].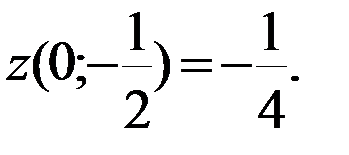

III участок: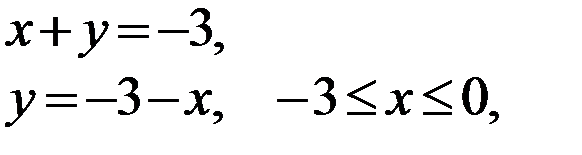

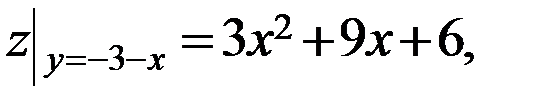
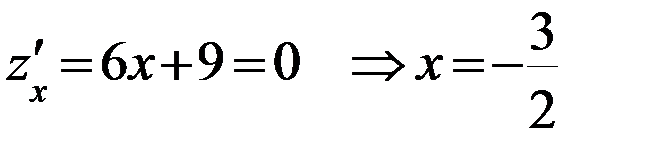- критическая точка, принадлежащая [-3;0].

Из всех вычисленных значений выберем наибольшее и наименьшее: 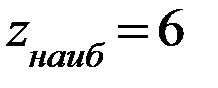в точках , -1 в точке .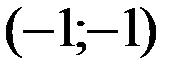

Задание 2Дана функция , точка и вектор .

Найти производную по направлению вектора 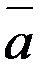в точке и .

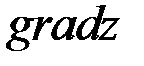Решение: Найдем направляющие косинусы вектора :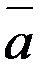

.

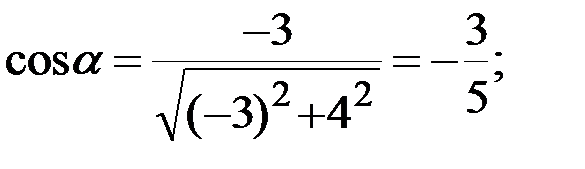
Далее находим значения частных производных от функции в точке :

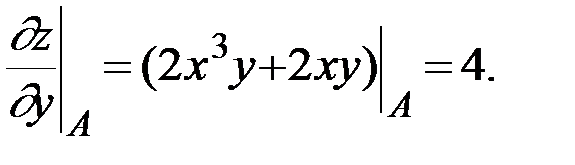
Наконец, вычисляем производную по направлению 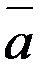в точке и градиент:

,

.

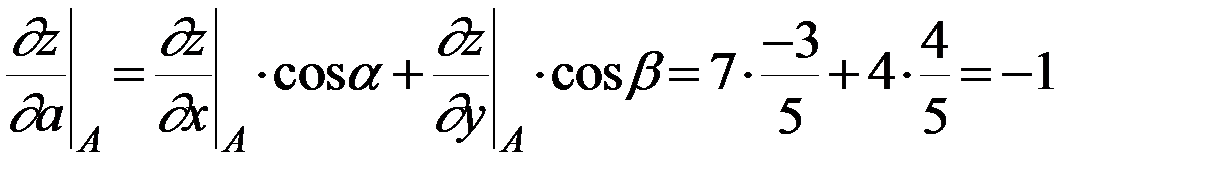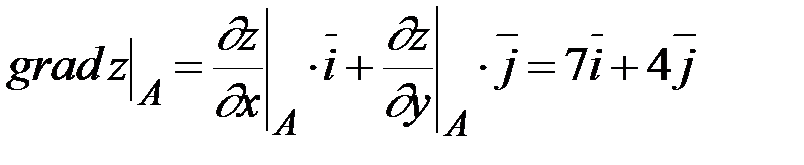Задание 3.Дана функция 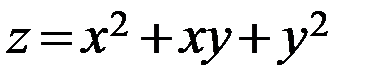, точка 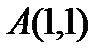и вектор 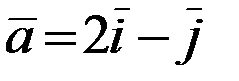. Найти: производную по направлению вектора в точке ; в этой точке.

Решение.

1.Для решение задачи воспользуемся формулой для нахождения производной от функции 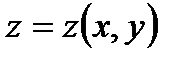в заданной точке 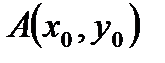по направлению вектора :

,

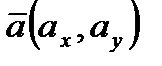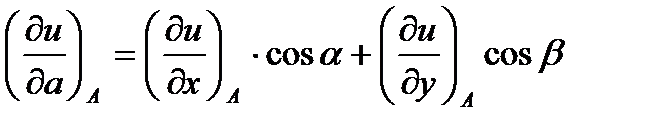где 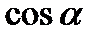, 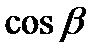- направляющие косинусы вектора 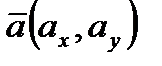, которые вычисляются по формулам: , .

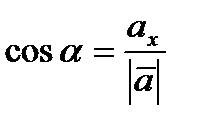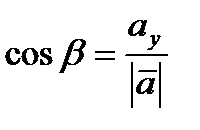По условиям задачи вектор 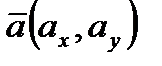имеет координаты 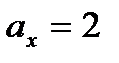, 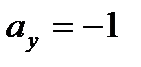. Тогда его длина равна: .

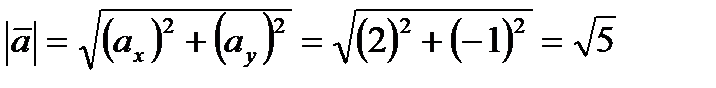Следовательно, для направляющих косинусов вектора получим следующие значения: , .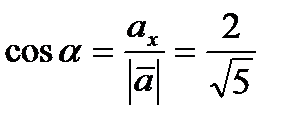

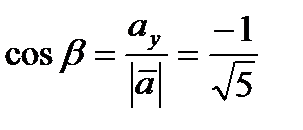Для решения задачи необходимо найти все частные производные первого порядка от функции :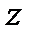

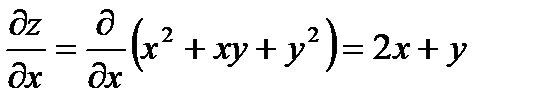
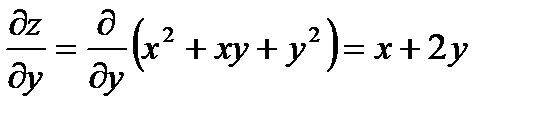
Вычислим значения этих частных производных первого порядка в точке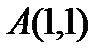

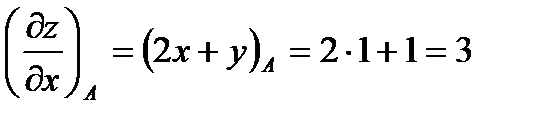
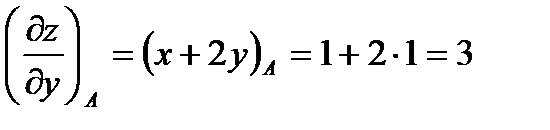
В заключении подставим полученные значения для направляющих косинусов вектора 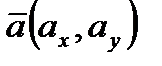и значения частных производных первого порядка от функции z в точке 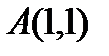в формулу производной по направлению в заданной точке:

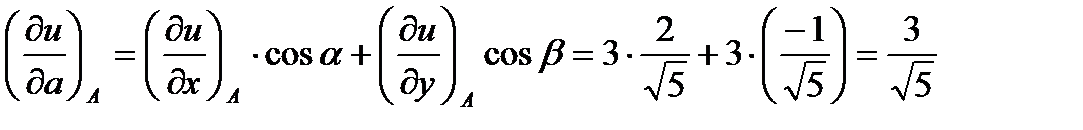
2.