Объективная субъективность: проективная геометрия

Столетия спустя, в эпоху Возрождения, вновь создаваемая культура заново открыла Платона. Она выполнила его завет по поиску Идеалов, при этом отказавшись от отрицания реального мира.

Художники и мастера – из числа людей – шли этим путем. Вызов, который они приняли, лежал в самой основе: как двумерное изображение может представить геометрию объектов в трехмерном пространстве? Это была реальная, практическая задача. Во времена, когда фотографии еще не существовало, а уже накапливались значительные личные состояния, заказчики хотели иметь картины, которые являлись бы постоянной летописью того, как они и их собственность выглядят в реальности.

На первый взгляд кажется, что в этом нет ничего общего с желанием Платона проникнуть сквозь видимую поверхностную сущность вещей в более глубокий слой реальности. Но все искусство художественной перспективы как раз и посвящено тому, как правильно передать видимое и поверхностное!

Есть, впрочем, некий смысл, в котором овладение видимостью вещей приближает нас к их сущности. Понимая, что одна и та же сцена может выглядеть по-разному в зависимости от точки зрения, с которой она передается, мы учимся отделять случайные элементы, зависящие от того, как посмотреть на вещь, от характерных особенностей самой вещи. Используя субъективность объективно, мы управляем ею.

Но довольно говорить абстрактно. Уже первые шаги в этой работе преподносят несколько восхитительных сюрпризов. Так давайте упростим задачу до ее основной сути, нарисовав сечения холста и ландшафта так, чтобы они выглядели как прямые линии (илл. 10).

Точки на нашем максимально упрощенном пейзаже – плоской горизонтальной поверхности, дающей в поперечном сечении прямую, – проецируют свет вдоль прямых линий к зрителю. Эти линии показаны пунктиром. Пройдя по ним до пересечения с холстом (место пересечения показано прямой вертикальной линией), мы определим, где различные точки пейзажа должны появиться на картине.

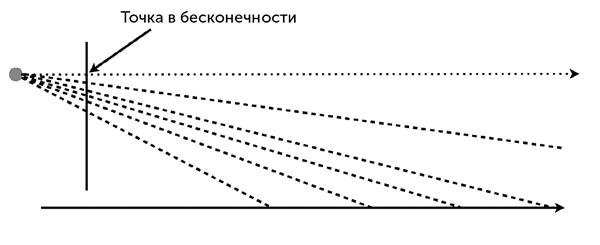
Илл. 10. Точки вдоль горизонтальной линии (пола) проецируются на участок прямой вдоль вертикальной линии (холста). Горизонтальная линия бесконечна, чего невозможно достичь в реальности, и тем не менее проецируется на реальную, конечную «точку бесконечности» на холсте.

Как вы можете видеть, точки, которые находятся дальше, проецируются на холст выше по вертикали. Но если мы будем рассматривать все более и более отдаленные точки, то, хотя они и будут на холсте располагаться одна над другой, промежутки между ними будут уменьшаться. Связывающие их лучи света достигают горизонтального предела, который на рисунке показан линией из точек. Эта линия не связана ни с какой реальной деталью ландшафта и тем не менее пересекает полотно в определенной точке.

Прямо на наших глазах на понятийном уровне происходит чудо – мы смогли поймать бесконечность! Когда мы смотрим на пейзаж, мы видим, что существует горизонт. Горизонт не существует в физической реальности, это – абстракция. Он представляет собой границу видимости и находится на бесконечном расстоянии. Тем не менее изображение линии горизонта на холсте, несомненно, реально. Это уникальная, особая точка – точка на бесконечности.

Дальнейшие чудеса ожидают нас после того, как мы возвратим и холст, и легший в его основу пейзаж (и равнину, и плоскость) в два измерения. Чтобы было проще, предположим, что холст и равнина перпендикулярны друг другу.

Теперь мы должны представить на пейзаже множество прямых линий. Каждая из них простирается до горизонта, и каждая проецирует соответствующую точку в бесконечности на холст. Тем не менее можно заметить, что параллельные линии на плоскости стремятся в одну и ту же точку на линии горизонта. Это наглядно показано на илл. 11.

Илл. 11. Параллельные прямые на линии горизонта встречаются в «точке схода», как ее обычно называют. Как только вы один раз обратите внимание на это явление, будете замечать его повсюду вокруг себя.

Мы называем эту точку точкой схода семейства параллельных линий в перспективе. Если говорить языком, который подходит для описания холстов, то мы можем сказать, что параллельные линии сходятся в точке бесконечности.

Здесь мистическая поэзия воплощается в прямом описании художественной реальности.

Различные семейства параллельных линий сходятся в различных точках, которые все вместе определяют горизонт. Спроецированный на холст, горизонт дает горизонтальную линию, представляющую его как собрание точек на бесконечности. Иными словами, концептуальный горизонт проецируется на холст как вполне реальная линия, лежащая в бесконечности.

Открытия, подобные этому, одновременно наполняли радостью и силой Брунеллески, одного из первых художников-ученых-инженеров эпохи Возрождения. Он превратил эти прозрения в мощную технику для создания реалистичных рисунков. Во время знаменитого эксперимента он использовал проективную геометрию, чтобы создать точное изображение того, как будет выглядеть баптистерий Сан-Джованни во Флоренции, если смотреть на него от входа в соседний собор, в то время только строившийся. Как показано на илл. 12, он сделал так, что зритель мог сравнить рисунок с настоящим баптистерием, отразив его в зеркале.

Изображение настоящего объекта появляется, если убрать зеркало, а для зрителя в рисунке оставлено небольшое отверстие.

Эта гениальная демонстрация произвела огромное впечатление на художников-современников, которые с энтузиазмом переняли технику Брунеллески и принялись ее энергично развивать. Вскоре роскошное пиршество перспективы породило такой шедевр, как «Передача ключей Святому Петру» Пьетро Перуджино (цветная вклейка G). Здесь перспектива играет активную роль, внося особое чувство порядка, гармонии и преклонения перед событием, основополагающим для Католической церкви. Эта фреска находится в Сикстинской капелле.

Нет лучше способа понять радость художника, открывшего перспективу и экспериментирующего с ней, чем разделить ее в одном из более простых творений. На цветной вклейке H я показал, как происходит процесс, благодаря которому вы можете в точной перспективе нарисовать пол, разделенный на квадраты, если посмотреть на него спереди и сверху, причем линии стремятся к бесконечно удаленному горизонту. Все, что вам нужно, – это карандаш, прямой край и ластик. (Под прямым краем имеется в виду линейка, на которой не нанесены метки расстояния. Разумеется, сгодится и обычная линейка – просто не обращайте внимания на деления!)

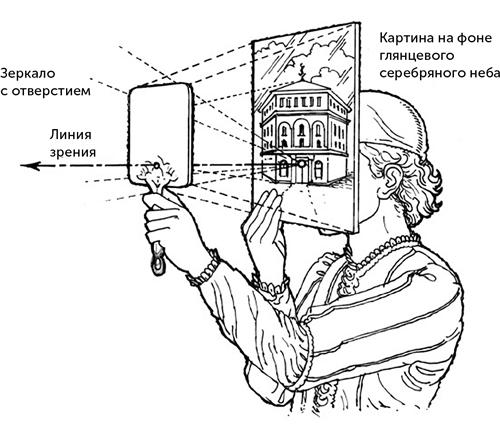
Илл. 12. Приспособление Брунеллески для сравнения рисунков, основанных на новом учении о перспективе, с реальностью

Процесс создания рисунка показан в верхней части вкладки. Мы проводим линию, отмеченную черным, – это будет горизонт. Начинаем с одного квадрата пола внизу, отмеченного синим. Конечно, рисовать квадрат не надо, поскольку мы смотрим на пол наискосок. Противоположные стороны «квадратов» после того, как будут продолжены, встретятся на линии горизонта, в точках схождения. Эти продолжения линий также показаны синим цветом. То есть начинаем мы вот с чего: одна плитка пола и линия горизонта. Трудность состоит в том, чтобы нарисовать все остальные одинаковые квадраты пола так, как они выглядели бы (в перспективе) для настоящего зрителя.

Самое главное наблюдение состоит в том, что диагонали квадратов также формируют семейство параллельных линий. Это семейство также сходится на линии горизонта, в своей собственной точке схождения. Мы можем продолжить красным цветом диагональ уже существующего квадрата, чтобы найти эту точку. А затем мы, обозначая новые линии оранжевым, вернемся назад уже от нее, чтобы отметить диагонали соседних квадратов! Найдя положения этих диагоналей, мы увидим, что пересечения оранжевых и синих линий – это вершины соседних квадратов. Желтые линии через эти вершины и соответствующие точки схождения, таким образом, составят стороны квадратов. Теперь мы можем продолжать: пересечения желтых линий «сторон» с оранжевыми «диагоналями» – это вершины новых квадратов… Продолжать можно так долго, как вам нравится, пока вы не потеряете терпение, или не сточится карандаш, или ваши квадраты не достигнут размеров атомов.

Чтобы закончить построение, вы можете просто стереть диагонали и (по желанию) сделать все линии одного цвета, как на рисунке внизу. Перспективное сокращение на этом рисунке очень велико, как будто мы смотрим на пол с точки зрения муравья – очень близко и с малой высоты. Это сделано, чтобы подчеркнуть, насколько могут на вид отличаться равные фигуры, такие как эти квадраты. Конечно, вы можете взять книгу и посмотреть на рисунок в разных ракурсах – вы увидите различные видимые размеры квадратов, но сетка пересечений будет оставаться одной и той же.

Я делал это построение раз десять или больше и каждый раз все еще чувствую возбуждение, когда у меня получается этот пол из квадратных плит. Это маленький, но подлинный акт творения.

Я испытываю те же чувства, какими наслаждается любой Мастер.

Я нашел, что ощущение этих основных идей перспективы открыло мне глаза. Если формулировать более точно, эти идеи привели мои глаза в более близкий контакт с моим внутренним сознанием. Я часто (особенно часто в городской обстановке) нахожу множество наборов (физически) параллельных прямых, убегающих вдаль к различным точкам схода. Когда я готов к таким вещам, мой опыт расширяется и становится более живым. Я надеюсь, что вы увидите, как нечто подобное произойдет с вами. С помощью тренированного воображения мы выходим за пределы Пещеры невежественных ощущений.

Вопросы перспективы: относительность, симметрия, инвариантность, дополнительность

Многие основные идеи современной фундаментальной физики совершенно незнакомы большинству людей. Они могут показаться абстрактными и неприступными, если представлять их обрывочно, в контекстах, отличающихся от их обычной среды обитания. По этой причине те из нас, кто пытается донести эти идеи до широкой аудитории, часто используют метафоры и аналогии. Найти метафоры, которые подходят к первоначальным идеям и одновременно доступны для понимания, – трудная задача. А еще труднее сделать это таким образом, чтобы можно было судить об их красоте. За эти годы я много раз сталкивался с данной проблемой и сейчас счастлив представить решение, которое принесло мне настоящее чувство удовлетворения.

• Проективная геометрия , это художественное изобретение эпохи Возрождения, содержит не просто метафоры, но подлинные модели из галереи больших, изящных и невероятно плодородных идей.

• Относительность – идея о том, что один и тот же объект может быть правильно и без всяких потерь представлен многими различными способами. В этом смысле относительность является самой сущностью проективной геометрии. Мы можем нарисовать одну и ту же сцену с многих разных ракурсов. Мы по-разному расположим в каждом случае краски на холсте, но различные картины будут нести одну и ту же информацию об объекте, просто по-разному закодированную.

• Симметрия – это идея, близко связанная с относительностью, но внимание здесь больше направлено на объект, а не на наблюдателя. Например, если мы поворачиваем объект, который рисуем, то с любого определенного ракурса он будет выглядеть иначе. Но его проективное описание, т. е. вся совокупность видов со всех возможных перспектив, остается прежним (потому что художники могут перемещать свои мольберты, чтобы уравновесить вращение). Подводя итоги, можно сказать, что вращение объекта – это симметрия его проективного описания. Мы можем изменить объект, вращая его, не меняя его проективное описание. Как мы еще и еще подчеркнем в нашем дальнейшем повествовании, Изменение без Изменения – это сущность симметрии.

• Инвариантность – это противоположность относительности. Различные аспекты объекта при изменении перспективы могут быть представлены по-разному, но некоторые характерные черты остаются общими для всех этих представлений. Например, прямые линии объекта всегда, с любой перспективы будут выглядеть прямыми линиями (хотя их направление и положение на холсте будут различаться). Или если в объекте пересекается три прямые линии, то их образы будут встречаться в одной точке с любой перспективы. Черты, которые являются общими для всех представлений, называются инвариантами. Инвариантные качества чрезвычайно важны, потому что они определяют характерные черты предмета, которые сохраняются в любой перспективе.

• Дополнительность (комплементарность) – это усиление относительности. Это один из глубинных принципов квантовой теории, но его важность как способа проникнуть вглубь вещей простирается далеко за границы физики. (Я полагаю, что дополнительность является гениальным метафизическим прозрением – и это на самом деле редкость.)

На самом простом уровне дополнительность означает, что в принципе может существовать множество различных точек зрения на некоторый объект, которые одинаково правомерны, но для того, чтобы наблюдать (или нарисовать, или описать) объект, вы должны выбрать только одну определенную точку.

Если бы на этом все заканчивалось, то дополнительность была бы небольшим частным случаем относительности. Новизна, которая появилась в квантовой теории, гласит, что в общем случае два квантовых портретиста не смогут нарисовать один и тот же объект в одно и то же время с разных ракурсов. Поскольку в квантовом мире мы должны принимать в расчет то, что наблюдение – это активный процесс, при котором нам приходится взаимодействовать с объектом.

Давайте, например, попробуем увидеть электрон. Чтобы это сделать, мы должны облучить электрон светом (или рентгеновскими лучами). Но свет передает электрону энергию и импульс и, следовательно, нарушает его местоположение, которое мы как раз и пытались определить!

Приняв необходимые предосторожности и совершив с электроном кое-какие необходимые манипуляции, мы можем провести наши измерения так, чтобы получить некоторые аспекты правильной информации о нашем объекте. Но другой информацией придется пожертвовать, поскольку она разрушается в процессе наблюдения. Сделав другие приготовления и предприняв другие предосторожности, мы сможем сделать иной выбор между тем, за чем наблюдать и чем пожертвовать, но самого этого выбора избежать не можем. Изображая квантовый мир, мы должны выбирать одну из всех возможных перспектив и работать, чтобы достичь ее. Если другой художник также работает, совершая манипуляции с нашим электроном своим собственным способом и преследуя свои цели, он исказит наше видение и уничтожит наш портрет, а мы уничтожим его рисунок.

Более сложная формулировка дополнительности, которая выводит ее за пределы относительности, звучит так: существует множество одинаково достоверных точек зрения на один и тот же объект – их можно назвать перспективами в общем смысле этого слова, – но они взаимоисключают друг друга. В квантовом мире мы можем реализовать только одну перспективу в единицу времени. Квантовый кубизм существовать не может.

Эти великие идеи – относительность, симметрия, инвариантность, дополнительность – сочетаются в сердце современной физики. Они должны бы находиться и в центре современной философии и религии, но этого пока нет. Во всех этих контекстах они иногда появляются в чуждых и абстрактных формах, которые могут сбить с толку. В такой ситуации вспомните о чудесном средстве – мысленно вернитесь к проективной геометрии, где вы сможете вновь увидеть их воплощенными в материальных, прекрасных художественных образах.