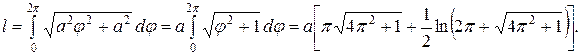Вычисление площади плоской области.

Теорема 24(вычисление площади области в декартовойсистеме координат). Если f(x) определена, непрерывна и неотрицательна на отрезке [a,b], то площадь множества выражается формулой:

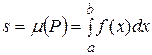. (16)

Множество Р называется криволинейной трапецией, порожденной графиком функции f(x) на [a,b].

□ Пусть 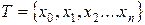некоторое разбиение [a,b]. Обозначим

∆x_i =x_i - x_i-1; ∆_i =[x_i-1, x_i]; h(T)= 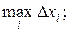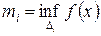; 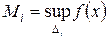(i=1,2…n).

Также обозначим через p(T) и P(T) – множества, составленные из прямоугольников

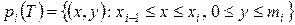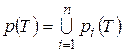; ; (17)

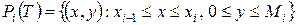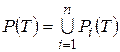; . (18)

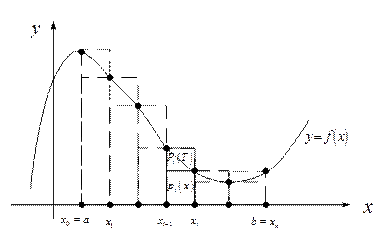
Рис.2

Поскольку 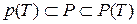, для любого разбиения T имеют место неравенства

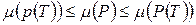. (19)

Из (17) и (18) получим, что .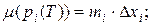

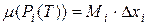Отсюда, т.к. прямоугольник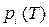и и 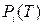не имеют общих внутренних точек, следует что

;

.

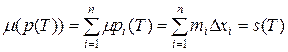Следовательно, площади многоугольников p(T) и P(T) равны соответственно нижней и верхним суммам Дарбу функции f(x) на [a,b]. Поэтому из (19) следует, что 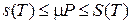. Но, т.к. f(x) непрерывна на [a,b], то она интегрируема на этом отрезке, следовательно

.

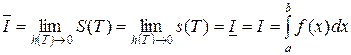По критерию интегрируемости верхний и нижний интеграл Дарбу совпадают и равны интегралу от f(x) по [a,b] (см. замечание к критерию интегрируемости). Переходя к пределу при h(T)→0 в неравенствах (19), получим

.

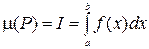Следствие 1. Если функция f(x) непрерывная и неположительная на отрезке [a,b] и P={(x,y): a≤x≤b, f(x)≤y≤0}, то

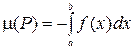. (20)

□ Положим 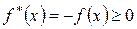. Тогда множество P* симметрично множеству P относительно оси Ox. Тогда в силу (16):

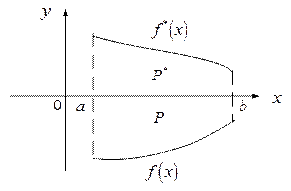
Рис.3

.

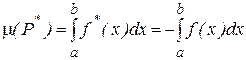Но μ(P*)=μ(P), тогда справедлива формула (20). ■ Следствие 2.Формулы (16) и (20) можно объединить в одну формулу. Если f(x) непрерывна и знакопеременна на [a,b] , то площадь множества, заключенного между графиком функции и осью OX равна:

.

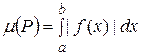Примеры. 1) Вычислить площадь, образованную одной аркой синусоиды.

Решение. Область имеет вид (рис.4)

Рис.4

.

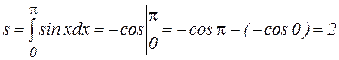2)Вычислить площадь множества, ограниченного эллипсом.

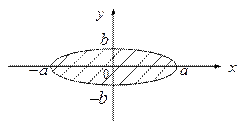
Рис.5

Решение. Из канонического уравнения эллипса имеем:

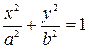
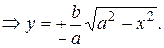
Тогда площадь будет равна: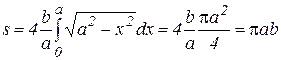

Следствие 3. Если функции f(x) и g(x) определены и непрерывны на [a,b], причем f(x)≥g(x) x 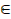[a,b], то площадь области P, заключенной между графиками функций f(x), g(x) и прямыми x=a, x=b , равна:

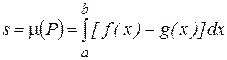. (21)

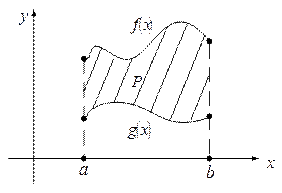
Рис.6

□ Пусть сначала f(x)≥g(x); f(x)≥0 и g(x)≥0. По теореме, площадь множества Р равна разности площадей криволинейных трапеций, порожденных графиками f(x) и g(x)

.

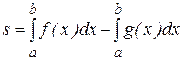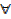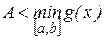Отсюда, учитывая линейное свойство интегралов, получается формула (21). Теперь пусть f(x) и g(x) имеют произвольные знаки на [a,b], но f(x)≤g(x) x [a,b]. Пусть число . Сделаем замену: y’=y+A.

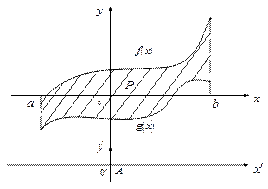
Рис. 7

В системе координат (x, y’) площадь фигуры ограниченную функциями f(x)+A и g(x)+A назовем P’. Ясно, что P’=P. Вычислим μ( Р’) в (x,y’), учитывая, что f(x)+A≥0 и g(x)+A≥0, по формуле (21) имеем:

.

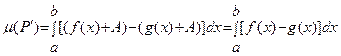Но, т.к. μ(P)= 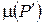, то . ■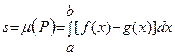

Пример.Найти площадь области, ограниченной кривымиy=x и y=x²-2.

Решение. Найдем точки пересечения кривых.

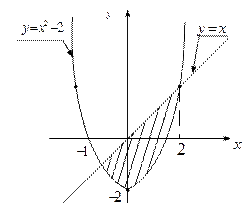
Рис.8

Приравнивая ординаты, получим: x²-2=x 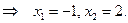Тогда площадь будет равна

.

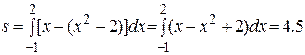Теорема 25(вычисление площади множества в полярной системе координат). Если функция 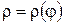определена и непрерывна на отрезке [α,β], то площадь множества P={( 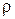φ,): α≤φ≤β, 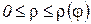}, граница которой в полярной системе координат задана графиком r(φ) и лучами φ=α и φ=β (которые могут превращаться в точки) определяется по формуле:

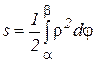(22)

□ Возьмем разбиение 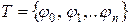отрезка [α,β], где φ₀=α, φ_n=β, и положим

∆φ_i= φ_i - φ_i-1, ∆_i=[ φ_i-1, φ_i], 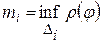, , 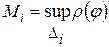и h(T)= .

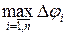Выберем произвольные точки 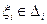. Тогда p_i(T)={(φ, 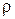): φ_i-1≤φ≤φ_i, 0≤ 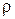≤m_i} и P_i(T)={(φ,r): φ_i-1≤φ≤φ_i, 0≤ 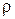≤M_i} круговые секторы с углом ∆φ_i­, i=1,2….n и радиусами m_i и M_i.

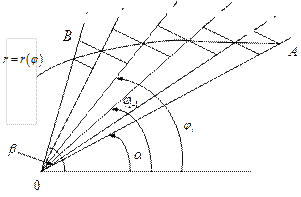
Рис.9

Обозначим 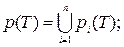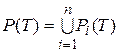ступенчатые фигуры, составленные из секторов p_i(T) и P_i(T), соответственно вписанные в P и описанные около множества Т. Тогда

p(T) P P(T) => μ(p(T))≤μ(P)≤μ(P(T)).

По формуле для площади сектора имеем:

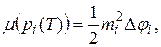
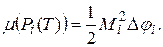
Поэтому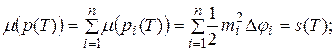

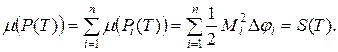
Здесь s(T) и S(T) – суммы Дарбу для функции 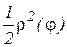. Тогда выполняется неравенство

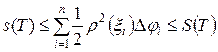, (23)

где 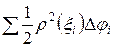- интегральная сумма для функции 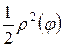на отрезке 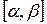. Так как функция 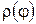непрерывна на 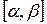, то 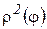тоже непрерывна и интегрируема на отрезке [a,b], а следовательно, выполняется критерий

.

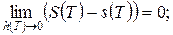
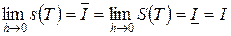Переходя в (23) к пределу при 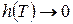, по теореме сравнения получим, что справедлива формула (22). ■

Пример. Найти площадь множества Р, ограниченного кривой 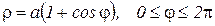, которая называется кардиоидой .

.

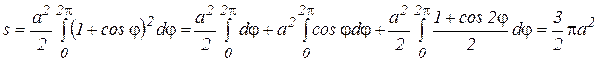Теорема 26 (вычисление площади множества, ограниченного кривой, заданной параметрически). Площадь множества, ограниченного простой гладкой замкнутой кривой 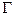, заданной параметрическими уравнениями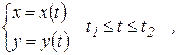

причем 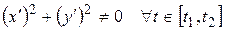, определяется по формуле

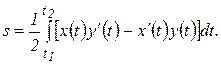(24)

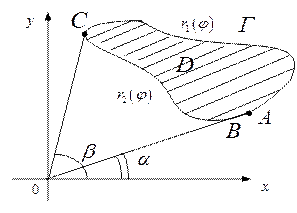
Рис.10.

□ Для доказательства воспользуемся формулой (22). Рассмотрим полярную систему координат. Пусть А и С крайние точки 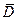, соответствующие полярным координатам 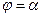и 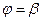, причем точке А соответствует значение параметра 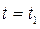начало кривой Г, а значение 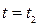- соответствуют точке В – конец замкнутой кривой Г. Пусть 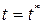соответствуют точке С. Из параметрических уравнений кривой Г и уравнений полярных координат в декартовой системе координат имеем

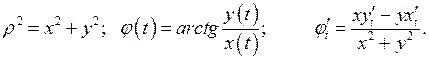
Площадь 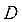в полярной системе координат равна разности площадей двух криволинейных секторов 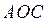и 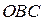. По формуле (22), предполагая, что 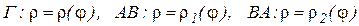, получим

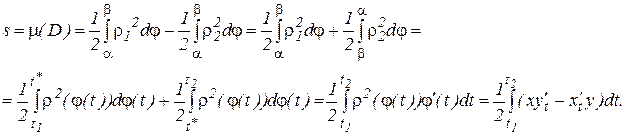
В силу. ■

Пример.Вычислить площадь, ограниченную эллипсом пользуясь формулой (24).

Решение. Запишемуравнение эллипса в параметрическом виде:

.

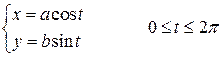Тогда по формуле (24) имеем:

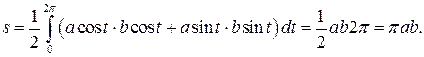
Вычисление длины кривой.Пусть Г – кривая на плоскости или в пространстве, заданная непрерывно дифференцируемой векторной функцией 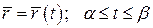, т.е.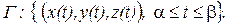

По определению, длиной кривой называется верхняя грань длин всевозможных ломанных вписанных в эту кривую, т.е. 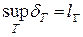и, если 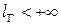, то кривая называется спрямляемой, и имеет конечную длину. Переменная длина дуги кривой 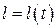, отсчитываемая от начала кривой Г, является возрастающей непрерывно дифференцируемой функцией параметра t и ее производная равна

.

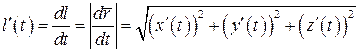Тогда длина кривой Г будет равна

.

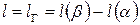По формуле Ньютона-Лейбница имеем

.

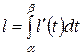а) Если Г пространственная кривая, то

.

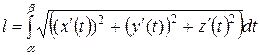б) Если Г – плоская кривая, заданная параметрически уравнениями

,

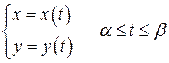то 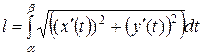(25)

в) Если Г кривая является графиком функции y=f(x) на 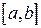, то параметризуя ее уравнение 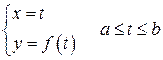, из (25) будем иметь:

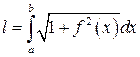(26)

г) Пусть кривая Г задана в полярной системе координат уравнением 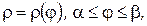, причем функции 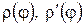непрерывны на 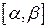. Уравнение кривой можно параметризовать, используя связь декартовой системы координат и полярной, приняв за параметр угол :

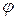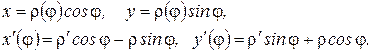
Подставим в (25) и, после преобразований, получим

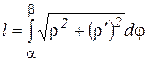(27)

Примеры. 1) Вычислить длину дуги верхней ветви полукубической параболы 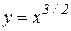, если .

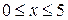Решение. Из уравнения 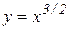находим: 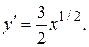Следовательно, по формуле (26) получим

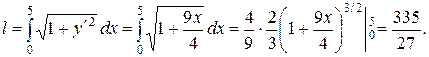
2) Вычислить длину дуги одной арки циклоиды .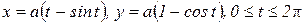

Решение. Из уравнений циклоиды находим:

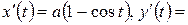
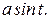
Когда переменная изменяется на отрезке 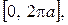то параметр 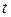принимает значения на отрезке 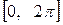. Следовательно, искомая длина дуги будет равна:

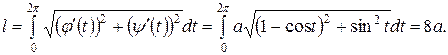
3) Вычислить длину первого витка спирали Архимеда: .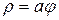

Решение. Первый виток спирали образуется при изменении полярного угла 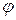от 0 до 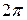. Поэтому по формуле (26) искомая длина дуги равна