Свойства интегрируемых функций

Теорема 6. Если функция f(x) интегрируема на отрезке , то она интегрируема на любом отрезке .

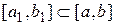□ Пусть ε > 0 произвольное число. Поскольку f(x) интегрируема на , то существует разбиение Т, такое что

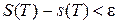(10)

Если 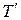разбиение , получено по разбиению Т добавлением точек 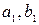, а 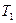- разбиение 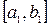образованное точками разбиения 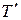, принадлежащему отрезку 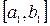. Тогда

.

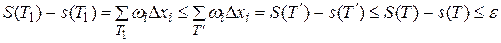Оценки верны, поскольку в последнем неравенстве первая сумма содержит неотрицательные слагаемые, соответствующие разбиению 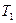, а вторая – слагаемые, соответствующие разбиению 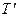, причем каждое слагаемое первой суммы входит во вторую сумму. Действительно, поскольку 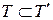, в силу (10) и свойства 2 сумм Дарбу имеем:

.

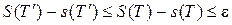Тогда по критерию интегрируемости, f(x) интегрируема на . ■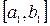

Теорема 7. Пусть 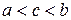. Тогда, если f(x)интегрируема на отрезках 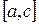и , то она интегрируема на отрезке 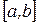, причем

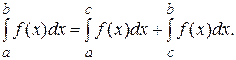(11)

□Пусть 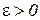, Т-разбиение , образованное точками разбиений иотрезков 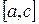и . По критерию интегрируемости разбиения и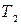можно выбрать так, чтобы

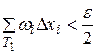и .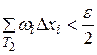

Очевидно, что 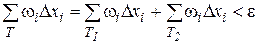и, следовательно,функция интегрируема по критерию интегрируемости.

Теперь докажем (11). Интегральную сумму для построенного разбиения Тможно записать .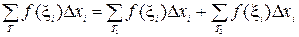

Переходя здесь к пределу при 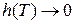( при этом 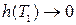, 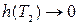), получим доказываемое равенство (11). ■

Формула (11) остается справедливой, если на отрезок [a,b] разбит на большее, чем два отрезка. Эта теорема называется свойством аддитивности определенного интеграла.

Теорема 8.Если f(x) и g(x) интегрируемы на отрезке , тогда их сумма также интегрируема на и справедливо равенство:

. (12)

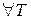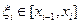□ отрезка и при любом выборе точек имеем

.

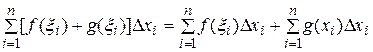В силу интегрируемости f(x) и g(x) существуют пределы интегральных сумм, стоящих в правой части, поэтому существует и предел левой части при h(Т)→0 и по определению определенного интеграла получим (12). ■

Теорема 9.Пусть f(x) интегрируема на и А - постоянная. Тогда функция Аf(x) также интегрируема на отрезке , причем

.

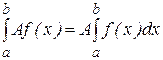□ Доказательство следует из равенств:

. ■

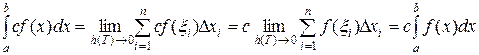Теорема 10.Пусть функции f(x) и g(x) определены на , причем f(x) интегрируема на , а g(x) отличается от f(x) в конечном числе точек. Тогда справедливо равенство:

.

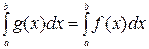□ Рассмотрим функцию 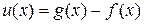. Очевидно 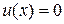на за исключением конечного числа точек, которые обозначим 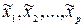. Положим . Пусть Т- разбиение. Тогда каждая из точек 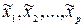принадлежит не более, чем двум отрезкам 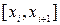( 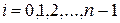) одновременно, а на остальных отрезках 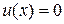, то для любого разбиения Т отрезка , при любом выборе точек 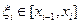имеем: .

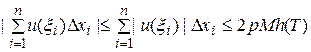Переходя в этом неравенстве к пределу при h(Т)→0 получим :

.

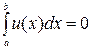В силу Т.8 функция 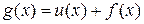интегрируема на и

. ■

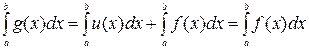Замечание.Определенный интеграл можно определить и для функций, заданных всюду на отрезке , за исключением конечного числа точек этого отрезка. Если доопределить функцию в этих точках произвольным образом, мы получим функцию, интегрируемую по Риману. В силу теоремы, интеграл не зависит от того какое значение принимает подынтегральная функция в этих точках.

Теорема 11.Если функции f(x) и g(x)интегрируемы на , то их произведение также интегрируемо на отрезке .

□ Без доказательства.

Теорема 12. Если функция f(x)интегрируема на и , то

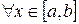
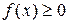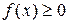
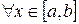. (13) □ Т.к. , то 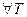отрезка 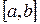и при любом выборе 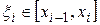будет справедливо неравенство . Переходя к пределу h(T) 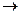0 получим (13). ■

Следствие.Если 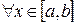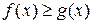и функции интегрируемы, то .

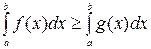Теорема 13. Если f(x) интегрируема на отрезке , то 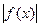также интегрируема на и выполняется неравенство:

.

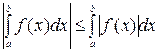□Из неравенства 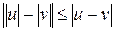следует, что колебание функции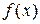 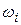на отрезке 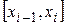не меньше колебания 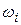функции 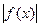на этом же отрезке, т.е. 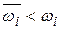. Т.к. f(x) интегрируема , то 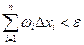. Тогда для разбиения Т получим 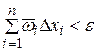, т.е. 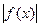интегрируемая. Пусть теперь Т- произвольное разбиение отрезка , тогда ,по свойству абсолютной величины имеем:

.

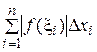Переходя к пределу h(T) 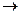0получим (13), в силу теоремы сравнения для пределов. ■

Замечание.Из интегрируемости 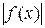на не следует интегрируемость f(x) . Например, функция 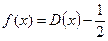, где 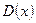- функция Дирихле, не является интегрируемой на т.к. 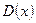не интегрируется, а функция 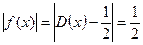интегрируемая.

Tеорема14.Если 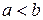и функция f(x)интегрируема на , то 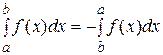, если 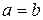, то .

□Пусть Т некоторое разбиение . Обозначим

.

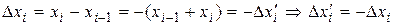Тогда

;

- . ■

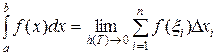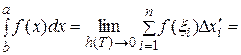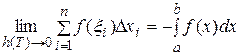Классы функций, интегрируемых по Риману. Выясним, какие функции можно интегрировать по Риману.

Теорема 15.Непрерывная на отрезке функция f(x) интегрируема по Риману на этом отрезке.

□В силу теоремы Кантора, непрерывная на отрезке функция равномерно непрерывна па этом отрезке, т.е. 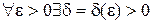, что на любом отрезке 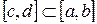, для которого 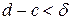, колебание будет удовлетворять неравенству:

< .

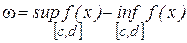Пусть Т разбиение отрезка с шагом 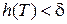. Тогда колебание на 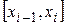удовлетворяет неравенству

.

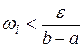Для этого разбиения имеем

.

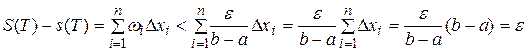Тогда согласно критерию интегрируемости функция f(x) интегрируема по Риману на . ■

Теорема 16.Ограниченная на отрезке функция f(x), имеющая на конечное число точек разрыва интегрируема на этом отрезке.

□Вначале рассмотрим случай, когда f(x) имеет единственную точку разрыва, причем точкой разрыва является один из концов отрезка. Пусть это точка а . Обозначим 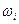колебание f(x)на 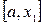. Зададим произвольное положительное число ε. Выберем точку x_1, чтобы .

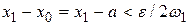На отрезке 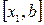функция непрерывна и следовательно интегрируема по Риману. По критерию интегрируемости найдется такое разбиение 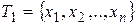отрезка 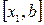, что 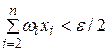. Для разбиения 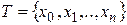отрезка в силу предыдущего, получим

.

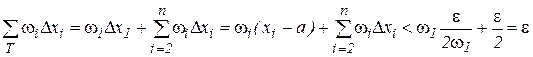По критерию интегрируемости это означает, что f(x) интегрируема на . Аналогично, если точка разрыва при 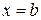. Рассмотрим общий случай. Пусть 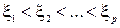точки разрыва f(x) на (a,b). Выберем точки 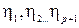, так чтобы выполнялось неравенства

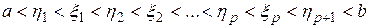. На каждом из отрезков 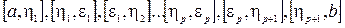функция интегрируема в силу предыдущего рассуждения, т.к. имеет не более одной точки разрыва. Тогда она интегрируема по Риману и на всем отрезке в силу свойства аддитивности. ■

Функция f(x) называется кусочно-непрерывнойнаотрезке если она имеет на этом отрезке не более конечного числа точек разрыва 1-го рода. Тогда теорема может быть сформулирована так: кусочно-непрерывная на отрезке функция f(x)интегрируема на нем.

Теорема 17.Монотонная на отрезке функция f(x) интегрируема по Риману на этом отрезке.

□Для определенности будем считать, что f(x) не убывает. Зададим произвольное 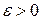. Пусть Т - разбиение с шагом 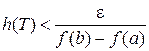. Очевидно, что в силу монотонности . Поэтому, проверяя критерий интегрируемости, получаем

. ■

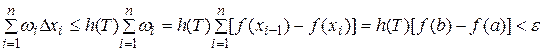Теорема 18.Ограниченная на отрезке функция f(x), имеющая счетное множество точек разрыва, интегрируема по Риману на этом отрезке.

□Без доказательства.

Таким образом, интегрируемыми по Риману функциями являются следующие функции: непрерывные; ограниченные с конечным числом точек разрыва; монотонные; ограниченные, имеющие счетное множество точек.

Теоремы о среднем для интеграла Римана.Имеют место важные для оценок интегралов теоремы.

Теорема19. Пусть выполняется условия:

1) функции f(x)и g(x) интегрируемы на отрезке ;

2) ;

3) ;

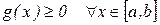тогда справедлива формула

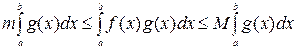(14)

□Произведение 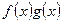интегрируемо на по теореме 11. Тогда, интегрируя почленно неравенство 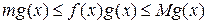, получим формулу. ■

Следствие. При условиях теоремы, если 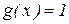, справедлива формула:

.

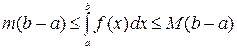Теорема 20 (обобщенная теорема о среднем).Пусть выполняются условия

1) функция f(x) непрерывная на отрезке ;

2) g(x)интегрируема на ;

3) .

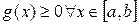Тогда 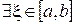, что справедлива формула среднего значения:

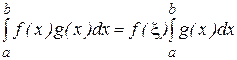(15)

□Поскольку функции интегрируемы на отрезке , то справедливы неравенства (14). Если 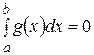, то из (14) следует, что 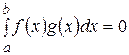и формула (15) будет выполняться 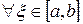. Пусть 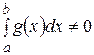, тогда из (14) получим:

.

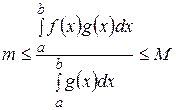Так как f(x) непрерывна на , то по второй теореме Вейерштрасса 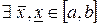, такие, что 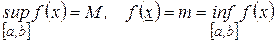. Тогда

.

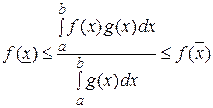В силу теоремы Коши для непрерывных на отрезке функций, непрерывная функция f(x) принимает все промежуточные значения между m и M. Поэтому существует точка

ξ є [a,b], в которой будет выполнятся равенство:

.

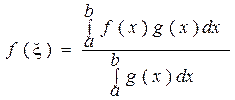Откуда следует формула (15). ■

Следствие (теорема о среднем). Если f(x) непрерывна на [a,b], то существует ξ є [a,b], такая, что

.

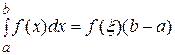Очевидно, что формула следует из (15) при g(x) ≡ 1.

Значение 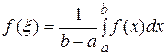- называется средним значением 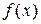на[a,b].

Замечание. Если f(x) не является непрерывной, то формула (15) в общем случае несправедлива. Действительно, пусть

; ;

;

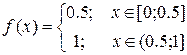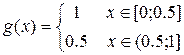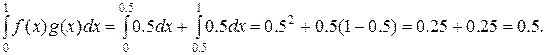
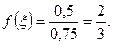
Однако точки ξ є [0,1], где f( 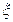) = 2/3 не существует.