Основные методы интегрирования

Метод преобразования подынтегрального выражения. Метод основан на преобразовании функции f(x) к такому виду, чтобы интеграл сводился к вычислению нескольких табличных интегралов.

Примеры.

1) .

2) .

3)

.

4)

.

5) .

6) .

7) .

8) .

9)

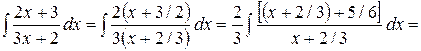
Одним из эффективных способов нахождения неопределенных интегралов является преобразование подынтегрального выражения с целью выделения дифференциала новой переменной интегрирования (простейшая замена переменной).

10)

.

11) .

12) , .

13) .

14) .

Метод замены переменной (метод подстановки).Имеет место следующая теорема, которая обосновывает метод:

Теорема 2.Пусть выполняются условия:

а) функция f(x) определена на промежутке ;

б) функция x= определена на промежутке Т и ;

в) непрерывна и дифференцируема на Т;

г) f(x) имеет первообразную F(x) на Х.

Тогда справедлива формула

. (1)

□ Функции f(x) и F(x) определены на Х. По условию , тогда имеют смысл сложные функции и . Поскольку F(x) есть первообразная для f(x) на Х, то 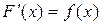. Функция по условию непрерывна и дифференцируема на промежутке Т. Поэтому непрерывна и дифференцируема на Т как сложная функция. Дифференцируем ее как сложную функцию:

.

Следовательно, имеет первообразную функцию . Откуда следует формула (1). ■

Запишем левую часть (1) по-другому:

.

Если , то получим формулу:

.

Применение этой формулы удобно, потому что вместо интеграла 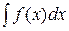, обозначив , получаем интеграл ,который вычислять проще, чем исходный.

Используя последнюю формулу, таблицу интегралов можно записать в более общем виде. Так, если некоторая переменная u является функцией переменной x, то есть , то справедливы формулы:

;

, ;

, ;

, ;

;

;

;

;

;

, ;

;

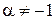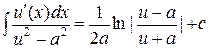,-a<u<a.

Примеры.1)

.

2)

.

3)

.

4)

Последний интеграл является табличным интегралом типа 8 или 9в зависимости от знака . Заменой вычисляются также следующие интегралы:

; ; .

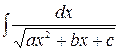5) Вычислить интеграл .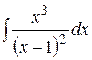

Решение. Положим 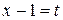, тогда . Отсюда . Тогда

.

Возвращаясь к переменной х, окончательно получаем

.

Замечание. При замене переменной в неопределенном интеграле иногда более удобно задавать не х как функцию 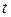, а, наоборот, задавать t как функцию от х.

6) Вычислить интеграл .

Решение. Положим 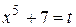, , тогда

,

так что

.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо хорошо владеть техникой дифференцирования и знать табличные интегралы.

7) Вычислить интеграл .

Решение. Положим , откуда . Таким образом,

,

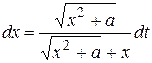так что

.

8) Вычислить интеграл .

Решение. Положим , . Тогда

9) Вычислить интеграл , .

Решение. Положим , , тогда

.

При аналогично получим

.

10) . Положим , тогда , . Имеем

.

11) . Положим , тогда , . Находим

, .

12) .

Положим , откуда . Значит,

, .

При интегрировании некоторых иррациональных функций часто используются тригонометрические подстановки.

13) 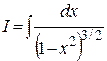. Положим , , тогда . Следовательно,

, .

14) . Положим , ; тогда . Поэтому

, .

Интегрирование по частям.Следующая теорема доказывает формулу интегрирования по частям.

Теорема 3. Если функции u(x) и v(x) непрерывны на промежутке Х, дифференцируемы во внутренних точках и существует интеграл , тогда на промежутке существует и интеграл 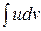, причём справедлива формула

или . (2)

Эта формула называется формулой интегрирования по частям.

□ На промежутке Х запишем формулу дифференцирования произведения для дифференциалов или . Интеграл от каждого слагаемого в правой части существует, т.к. , а - существует по условию. Тогда существует интеграл 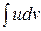, причем , или ■

Практика показывает, что большая часть интегралов, которые вычисляются по формуле интегрирования по частям, может быть разбита на 3 группы:

1) ; , где - многочлен m-й степени. Эти интегралы вычисляются путём m-кратного интегрирования по частям по формуле (2), причём каждый раз за u(x) обозначают многочлен, т.е. , а .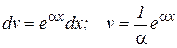

2) Интегралы, в которых подынтегральная функция содержит в качестве множителя одну из следующих функций: ln x, arcsin x, arccos x, arctgx, ln и т.д. Для вычисления интеграла за u(x) обозначают одну из указанных функций.

3) Интегралы вида: ; ; ; и т.д. Путём двукратного интегрирования по частям получают уравнение для данного интеграла.

Примеры.

1) .

2) .

3)

.

4)

.

Иногда для вычисления интеграла формулу интегрирования по частям приходится применять несколько раз.

5)

Таким образом, интеграл вычислен двукратным интегрированием по частям.

6) . Положим , . Тогда , . Откуда по формуле интегрирования по частям имеем

.

Таким образом, получилось линейное уравнение относительно , откуда находим .

7) В заключение вычислим интеграл 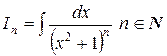, который понадобится в дальнейшем. При имеем табличный интеграл

Пусть . Представив 1 в числителе как разность , получим

Во втором интеграле применим метод интегрирования по частям:

,

тогда

следовательно,

откуда

Таким образом, интеграл выражен через интеграл :

Такие формулы называются рекуррентными формулами.

Разделы: 6.3. Интегрирование рациональных функций. 6.4. Интегрирование иррациональных и трансцендентных функций изучаются на практических занятиях и самостоятельно.