Закон изменения момента импульса.

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величинуL, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета. L = ΣL_i.

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы. dL/dt=M.Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что 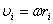, получим
.

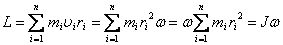Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):

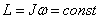
Момент инерции J (кгм²) –Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: .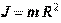

Момент инерции стержня:

Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс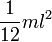
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец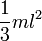

Момент инерции цилиндра :

Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра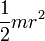
Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс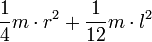

Момент инерции шара :

Шар радиуса r и массы m

Ось проходит через центр шара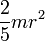

Теорема Штейнера :

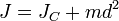
Формула выражает теорему Гюйгенса-Штейнера:

Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между этими осями.

Из теоремы следует, что наименьший момент инерции - это момент инерции относительно оси, проходящей через центр масс.

Закон сохранения момента импульса для вращательного движения

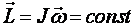при ;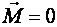

11)

Основное уравнение динамики вращательного движения твердого тела:

Второй закон Ньютона для вращательного движения

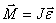
По определению угловое ускорение 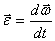и тогда это уравнение можно

переписать следующим образом

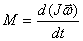
с учетом (5.9)

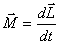
или

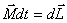(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 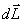, равно импульсу момента 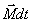всех внешних сил, действующих на это тело.

12)

Кинетическая энергияизмеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки.

При вращательном движении роль массы m выполняет момент инерции I, а вместо линейной скорости v выступает угловая скорость ω, и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:

,

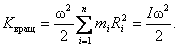(6.4.1)

Если тело вращается вокруг неподвижной оси z с угловой скоростью 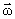, то линейная скорость i-й точки 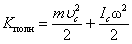, R_i – расстояние до оси вращения

Если произвольная м.т. вращается по окружности и на нее действует сила 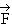,то при повороте на некоторый угол совершается элементарная работа dА = F ds, где ds=r dj. Тогда

dА =(r F) dj = M dj.

(5.18)

Полученное выражение остается справедливым и случае системы м.т., совершающих вращательное движение относительно оси z при w =сonst. В этом случае момент внутренних сил равен нулю и работа не совершается. Для нахождения полной работы необходимо вычислить интеграл

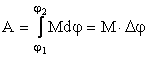
13)

Виды движения:

Имеется пять видов движения твердого тела:

1) Поступательное движение твёрдого тела - это такое его движение, при котором любая прямая, жёстко связанная с телом, перемещается, оставаясь параллельной своему

первоначальному направлению.

2)Вращательное движение твёрдого тела - это такое движение, при котором все его

точки движущиеся по окружностям, центры которых находятся вне пределов тела.

3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета.

4)сферическое, если одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета.

5)свободное, если нет перечисленных выше четырех ограничений.

Произвольное движение твердого тела складывается из поступательного движения и вращения. При равновесии для исключения возможности поступательного движения требуется равенство нулю суммы всех сил, а для исключения возможности вращения - равенство нулю суммы всех моментов.

Произвольное перемещение твердого тела из положения 1 в положение 2 можно представить как сумму двух перемещений — поступательного перемещения из положения в положение V или и поворота вокруг оси О или оси .Очевидно, что такое разбиение перемещения на поступательное и вращательное может быть осуществлено бесчисленным множеством способов, однако в любом случае производится поворот на один и тот же угол.

В соответствии со сказанным выше элементарное перемещение какой-либо точки тела можно разложить на два перемещения — «поступательное» и «вращательное»:

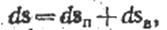
причем для всех точек тела одно и то же. Такое разложение перемещения можно, как мы видели, осуществить различными способами, причем в каждом случае вращательное перемещение осуществляется поворотом тела на один и тот же угол (но относительно различных осей), в то время как оказываются различными.

Разделив на соответствующий промежуток времена dt, получим скорость точки

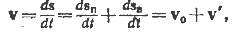
где v — одинаковая для всех точек тела скорость поступательного движения и v — различная для разных точек тела скорость, обусловленная вращением.