Несобственные интегралы от неограниченных функций.
Такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 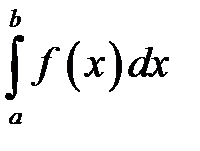 . Но, в отличие от определенного интеграла, подынтегральная функция
. Но, в отличие от определенного интеграла, подынтегральная функция 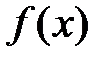 терпит разрыв второго рода:
терпит разрыв второго рода:
1) в точке 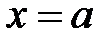 , 2) или в точке
, 2) или в точке 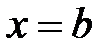 ,
,
3) или в обеих точках сразу, 4) или даже на отрезке интегрирования.
Определение 2.Пусть 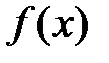 определена на
определена на 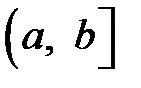 , причем
, причем 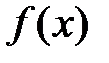 неограниченна в окрестности особой точки
неограниченна в окрестности особой точки 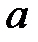 , но она ограничена и интегрируема на любом отрезке
, но она ограничена и интегрируема на любом отрезке 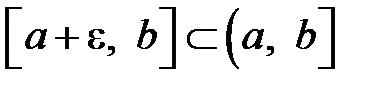 . Тогда если существует предел
. Тогда если существует предел 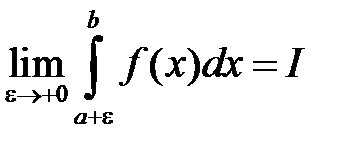 , то он называется несобственным интегралом и обозначается
, то он называется несобственным интегралом и обозначается 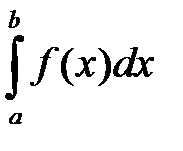 .
.
Если предела нет или он равен бесконечности, то интеграл называется расходящимся.
Аналогично определяется интеграл от функции, неограниченной на верхнем пределе интегрирования: 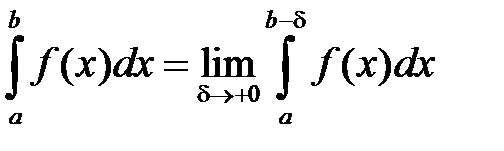 . Наконец, если
. Наконец, если 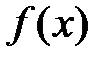 неограниченна в окрестности особой точки
неограниченна в окрестности особой точки 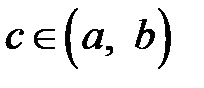 , то
, то
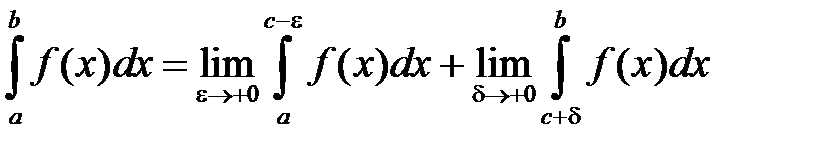 .
.
Свойства несобственных интегралов.
Если сходятся интегралы 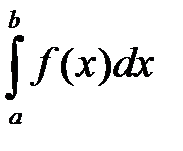 и
и 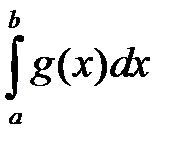 , где
, где 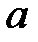 и
и 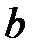 могут принимать значения
могут принимать значения 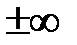 , то
, то
1. 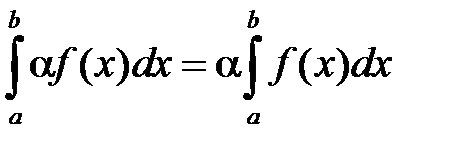 , где
, где 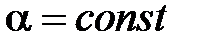 .
.
-
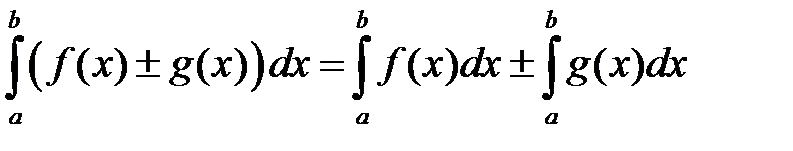 .
.
Несобственные интегралы в левых частях сходятся, и их значения равны выражениям в правых частях.
Рассмотрим 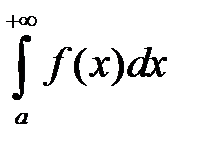 . Пусть
. Пусть 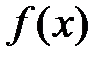 непрерывна на любом отрезке вида
непрерывна на любом отрезке вида 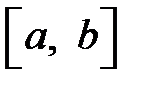 , где
, где 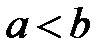 . Тогда интегралы
. Тогда интегралы 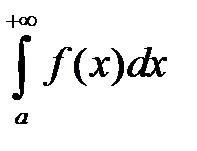 и
и 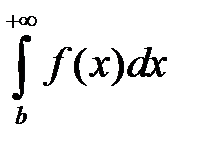 сходятся или расходятся одновременно. Аналогичное утверждение можно сформулировать и для несобственных интегралов от неограниченных функций и конечного отрезка интегрирования.
сходятся или расходятся одновременно. Аналогичное утверждение можно сформулировать и для несобственных интегралов от неограниченных функций и конечного отрезка интегрирования.
23. необходимые условия сходимости несобственных интегралов. Критерий Коши. Абсолютно и не абсолютно сходящейся несобственные интегралы. Главное значение расходящегося несобственного интеграла.
Формулировки приводятся для интегралов вида 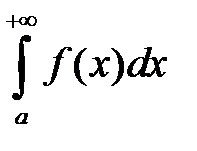 , но легко распространяются и на несобственные интегралы других типов.
, но легко распространяются и на несобственные интегралы других типов.
Определение 3.Несобственный интеграл 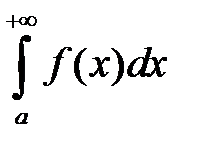 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 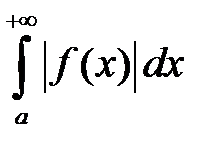 .
.
Определение 4. Если интеграл 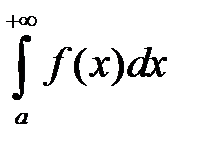 сходится, а интеграл
сходится, а интеграл 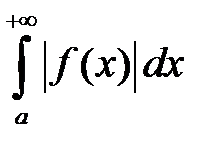 – расходится, то интеграл
– расходится, то интеграл 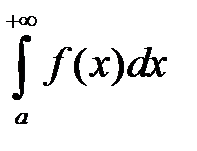 называется условно сходящимся.
называется условно сходящимся.
Теорема. Если 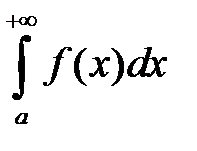 сходится абсолютно, то он сходится.
сходится абсолютно, то он сходится.
Признак Дирихле.Несобственный интеграл 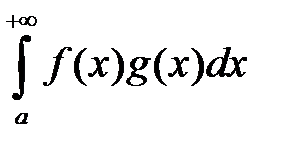 сходится, если выполняются следующие условия:
сходится, если выполняются следующие условия:
1) функция 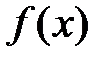 дифференцируема и монотонно стремится к нулю с ростом
дифференцируема и монотонно стремится к нулю с ростом 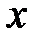 ;
;
2) функция 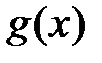 непрерывна и имеет ограниченную первообразную.
непрерывна и имеет ограниченную первообразную.
Примеры функций с ограниченной первообразной: 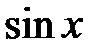 ,
, 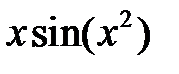 ,
, 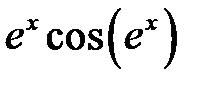 .
.
Признак Абеля. Несобственный интеграл 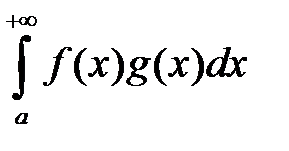 сходится, если выполняются следующие условия:
сходится, если выполняются следующие условия:
1) функция 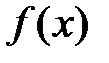 непрерывна на
непрерывна на 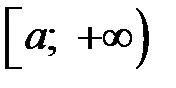 и
и 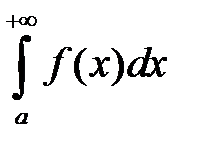 сходится;
сходится;
2) функция 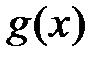 ограничена, непрерывно дифференцируема и монотонна на
ограничена, непрерывно дифференцируема и монотонна на 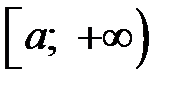 .
.
Утверждение. Если сходится интеграл 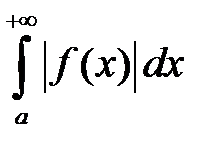 , то абсолютно сходятся интегралы
, то абсолютно сходятся интегралы 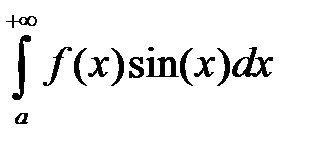 и
и 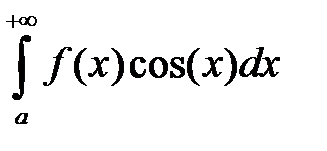 .
.
Пример 7.Интеграл Френеля 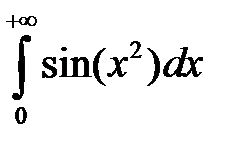 сходится, так как
сходится, так как
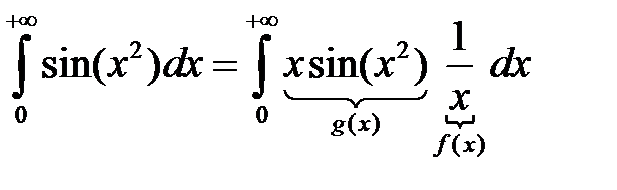 .
.
Пример 8. Интеграл Дирихле 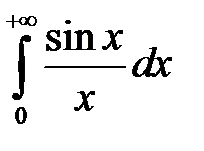 сходится условно.
сходится условно.
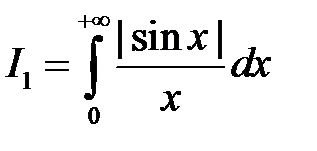 – расходится, так как
– расходится, так как 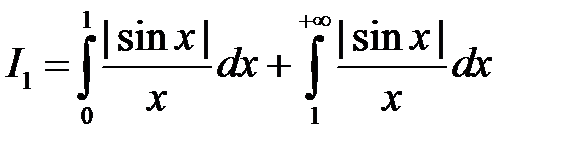 . Первый интеграл суммы сходится. Рассмотрим второй интеграл:
. Первый интеграл суммы сходится. Рассмотрим второй интеграл:
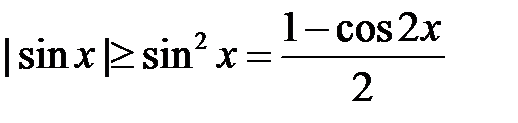 ,
,
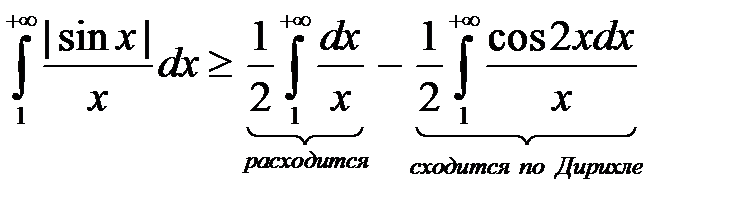 .
.
Интеграл 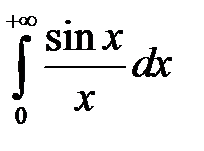 – сходится по признаку Дирихле:
– сходится по признаку Дирихле:
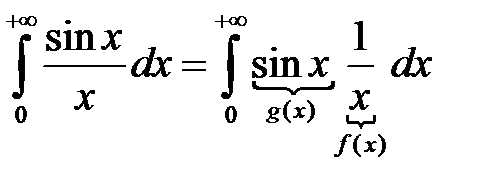 .
.
