Вывод формулы длины дуги регулярной кривой.

Лемма. Пусть жорданова кривая регулярна и l (t) – длина дуги этой кривой, ограниченной точками М(а) и М(b). Тогда функция l (t) дифференцируема на отрезке[a;b], причём для всех t имеем:

(8) .

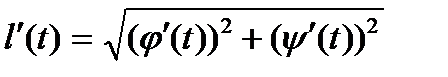Доказательство. Возьмём любое t 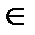[a;b] и дадим t приращение 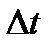такое, что t +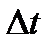 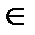[a;b]. Положим для определённости 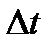> 0. Соответствующее приращение функции l (t), т.е. l (t + 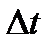) - l (t), равно длине дуги кривой, ограниченной точками М(t) и М(t + 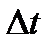). В силу неравенств (6) и (7) п.2 имеем:

.

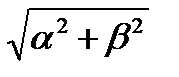
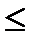
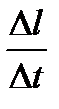
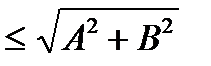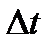
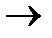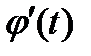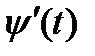Перейдём к пределу при 0. В силу непрерывности функций и в точке t получаем, что

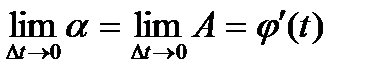
и

,

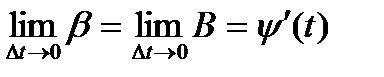а потому

.

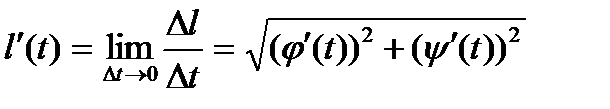Лемма доказана.

Из этой леммы следует, что

(9)

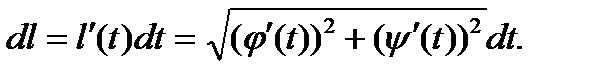
Так как 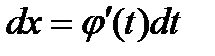, , 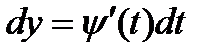то формулу (9) можно переписать в виде

.

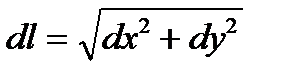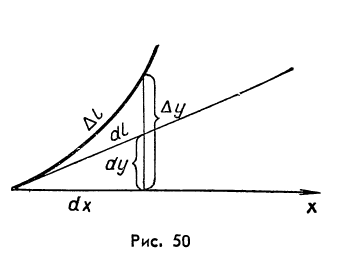
Геометрический смысл этой формулы ясен из рисунка 50, где 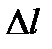- участок дуги, а 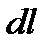- соответствующий отрезок касательной. Мы будем называть 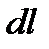дифференциалом длины дуги кривой.

Теорема 2. Если жорданова кривая Г:

,

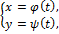
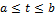Регулярна, то его длина выражается формулой

(10)

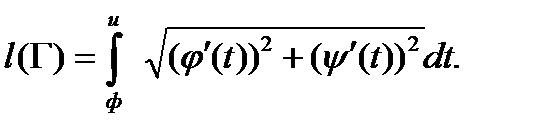
Доказательство. Так как 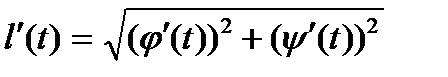, то 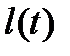- первообразная для 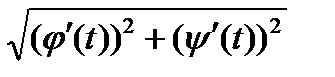, а тогда 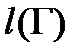равна разности значений первообразной, т.е.

l=l(a)-l(b)=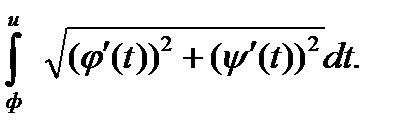

Теорема доказана.

Полученную формулу можно переписать в следующих видах:

(10')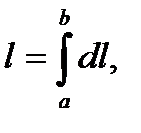

(10'')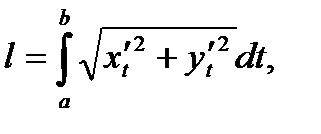

(10''')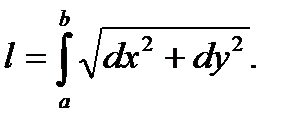

Пример 1. Рассмотрим длину дуги астроиды ,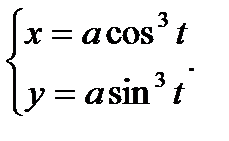

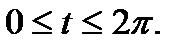
Решение. Данная кривая симметрична относительно обеих координатных осей, поэтому достаточно найти длину четверти дуги, расположенной в первом квадранте ( )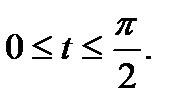

Найдём производные: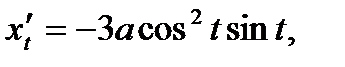

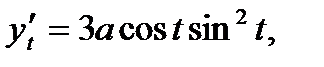
Вычислим сумму: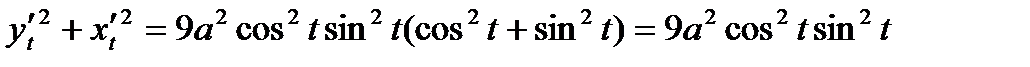

Учитывая сказанное выше, найдём четверть длины астроиды:

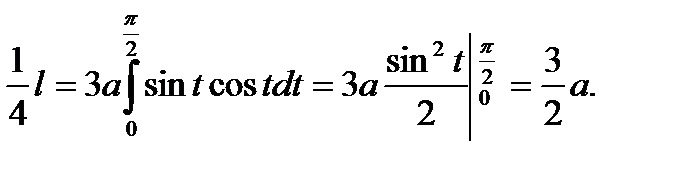
Длина всей кривой 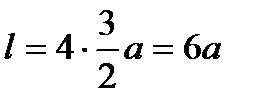. Она мало отличается от 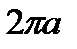, т.е. от длины окружности, описанной вокруг астроиды.

4. Частные случаи формулы длины кривой. Рассмотрим частные случаи общей формулы (10) п.3. Если кривая Г задана явным уравнением 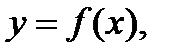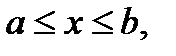то её можно представить параметрическими уравнениями

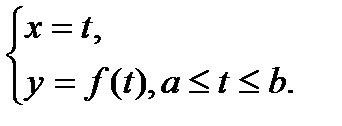
В этом случае

(11) .

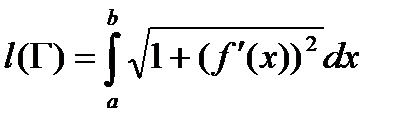Полученную формулу записывают короче в виде

(11')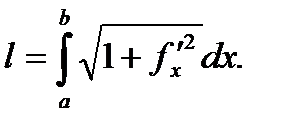

Значит,

(12)

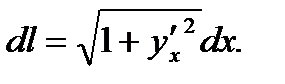
Пример 2. Вычислим длину дуги цепной линии 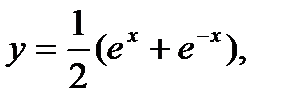взятой от точки х=0 до точки х=1 (рис.51).

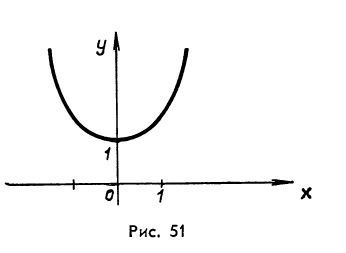
Найдём производную

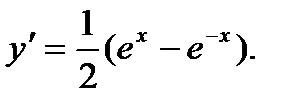
Вычислим подкоренное выражение

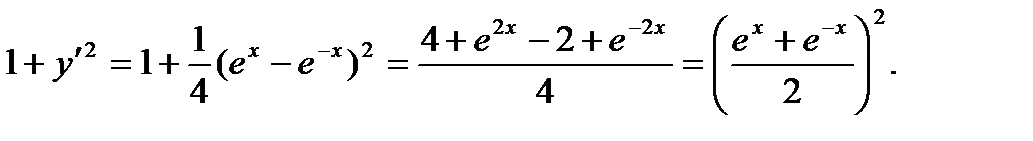
Длина l указанного отрезка цепной линии будет

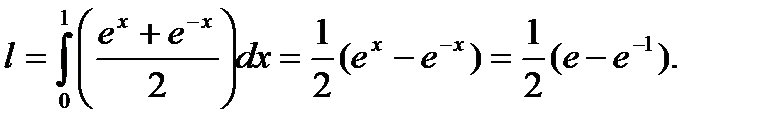
Рассмотрим теперь случай, когда кривая Г задана в полярных координатах уравнением 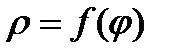, где 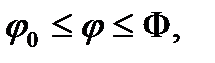причём функция 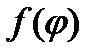на отрезке [ 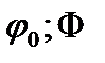] имеет непрерывную производную .

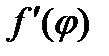Так как декартовы координаты связаны с полярными координатами точек плоскости соотношениями 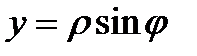, полярное уравнение данной кривой можно записать в виде параметрических уравнений:

, ;

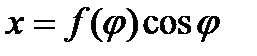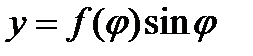отсюда находим:

,

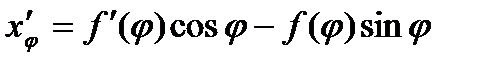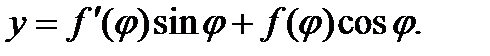
Поэтому

.

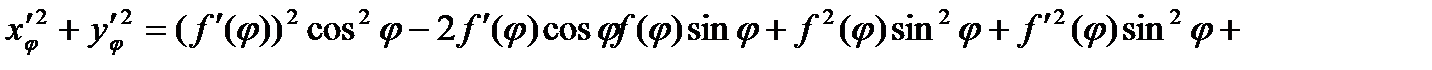
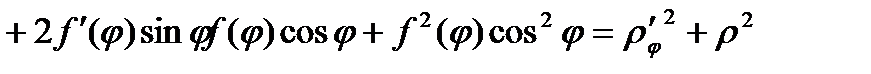В силу формулы (10) п.3 имеем:

(13)

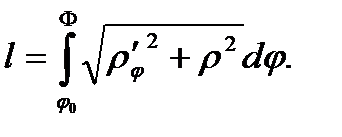
22 Несобственные интегралы от непрерывных функций на бесконечном промежутке и от неограниченных на отрезки функций. Основные определения и свойства.

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 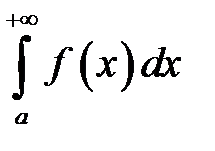. В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

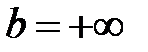Реже встречаются интегралы с бесконечным нижним пределом 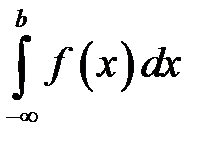или с двумя бесконечными пределами: .

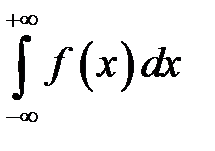Использование несобственных интегралов, позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.

Изобразим на чертеже график подынтегральной функции 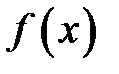. Типовой график и криволинейная трапеция для случая 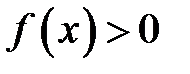выглядит так:

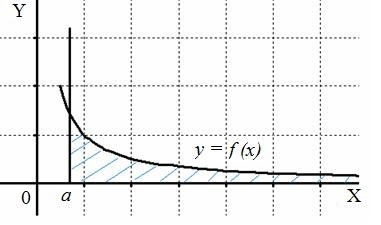
Несобственный интеграл 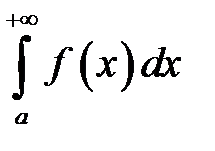численно равен площади заштрихованной фигуры, при этом возможны два случая:

1. Раз фигура бесконечная, то , иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится.

2. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться конечному числу! Например: 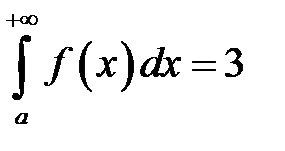. Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.

В каких случаях несобственный интеграл расходится, а в каких сходится? Это зависит от подынтегральной функции .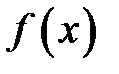

А что будет, если бесконечная криволинейная трапеция расположена ниже оси абсцисс? В этом случае, несобственный интеграл 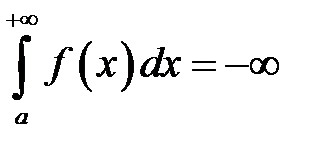(расходится) либо равен конечному отрицательному числу.

Мы рассматривали знакопостоянную функцию 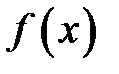для простоты интерпретации. На самом деле, подынтегральная функция может быть знакопеременной.

Определение 1.Пусть на интервале 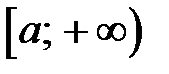задана функция 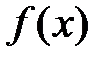, интегрируемая (следовательно, ограниченная) на любом отрезк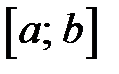е , где 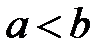. Тогда если существует 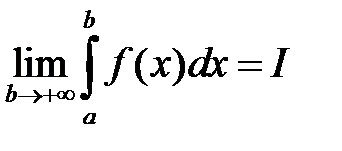, то он называется несобственным интегралом и обозначается .

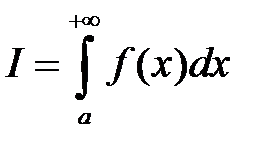Аналогично определяются:

,

.

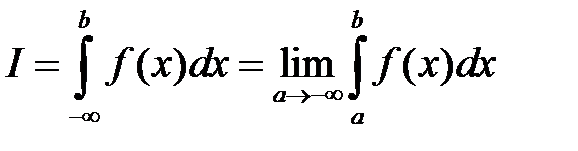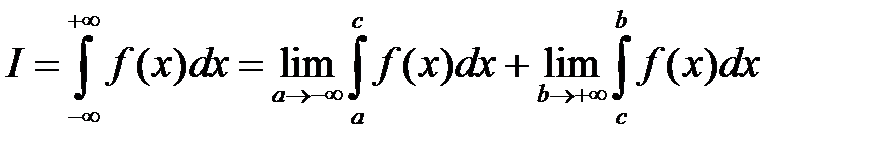В последнем случае предполагается, что 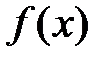интегрируема на любом отрезке; точку можно выбрать произвольно.

В чем отличие неопределенного интеграла от определенного? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.