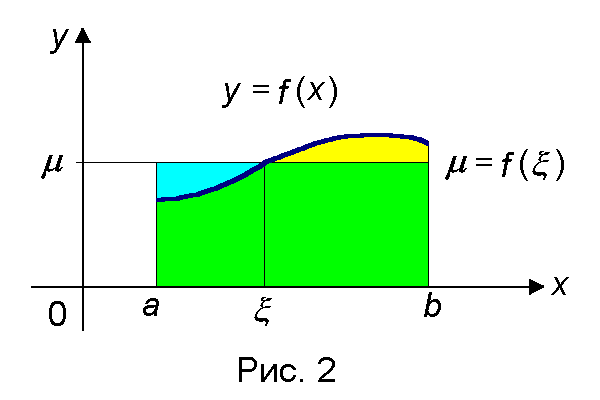
Геометрический смысл теоремы о среднем значении
Для непрерывной неотрицательной функции f(x) теорема о среднем значениии утверждает существование прямоугольника с основанием b − a и высотой, равной значению функции f(x) в некоторой точке ξ О [a,b], площадь которого равна площади криволинейной трапеции (рис. 2).
18. Интеграл с переменным верхним приделом его непрерывности и дифференцируемость. Основная теорема интегрального исчисления. Формула Ньютона – Лейбница
Определение функции 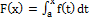 - определенного интеграла с переменным верхним пределом. Свойства функцииF(х): непрерывность и дифференцируемость. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница и её значение для интегрального исчисления. Связь между определенным и неопределенным интегралами функции.
- определенного интеграла с переменным верхним пределом. Свойства функцииF(х): непрерывность и дифференцируемость. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница и её значение для интегрального исчисления. Связь между определенным и неопределенным интегралами функции.
Пусть функция f(x) интегрируема на [a,b]. Тогда, 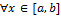 каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция
каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция 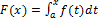 , которую называют интегралом с переменным верхним пределом.
, которую называют интегралом с переменным верхним пределом.
ДифференцируемостьF(x). Если f интегрируема на [a,b] и непрерывна в 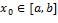 , то
, то 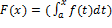 дифференцируема в
дифференцируема в 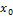 и
и 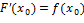 , но было установлено существование производной от интеграла спеременным верхним пределом и эта производная равна значению подынтегральной функции в точке, равной верхнему пределу, то есть
, но было установлено существование производной от интеграла спеременным верхним пределом и эта производная равна значению подынтегральной функции в точке, равной верхнему пределу, то есть 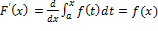 .
.
Непрерывность F(x). Если функция f(x) интегрируема на интервале 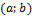 ( => интегрируема на любом сегменте, содержащихся в интервале
( => интегрируема на любом сегменте, содержащихся в интервале 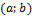 ), то интеграл с переменным верхним пределом представляет собой непрерывную на
), то интеграл с переменным верхним пределом представляет собой непрерывную на 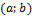 функцию от верхнего предела. Чтобы убедиться в этом, докажем, что приращение
функцию от верхнего предела. Чтобы убедиться в этом, докажем, что приращение 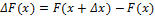 функции
функции 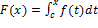 стремится к нулю при
стремится к нулю при 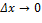 .
.
Th (существование первообразной для непрерывной функции).Любая непрерывная на интервале 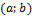 функция f(x) имеет на этом интервале первообразную. Одной из первообразных является функция
функция f(x) имеет на этом интервале первообразную. Одной из первообразных является функция 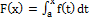 . Достаточно доказать, что для любого фиксированного x из интервала (a,b) существует предельное значение
. Достаточно доказать, что для любого фиксированного x из интервала (a,b) существует предельное значение 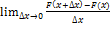 , причем это предельное значение равно f(x).
, причем это предельное значение равно f(x).
Th. Если 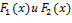 - любые первообразные для функции
- любые первообразные для функции 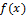 на интервале
на интервале 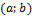 , то всюду на этом интервале
, то всюду на этом интервале 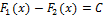 , где C - некоторая постоянная. Следствие. Если
, где C - некоторая постоянная. Следствие. Если 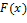 - одна из первообразных функций для функции
- одна из первообразных функций для функции 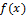 на интервале
на интервале 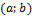 , то любая первообразная
, то любая первообразная 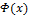 для функции
для функции 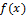 на
на 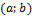 имеет вид
имеет вид 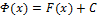 , где C - некоторая постоянная.
, где C - некоторая постоянная.
Формула Ньютона-Лейбница. Пусть функция f непрерывна на [a,b]. Если функция Ф является произвольной её первообразной на этом отрезке, то 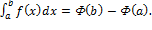 Т.к. любые две первообразные данной функции f(x) отличаются на постоянную, то согласно теореме существования первообразной для непрерывной функции можно утверждать, что любая первообразная Φ(x) непрерывной на сегменте [a,b] функции f(x) имеет вид
Т.к. любые две первообразные данной функции f(x) отличаются на постоянную, то согласно теореме существования первообразной для непрерывной функции можно утверждать, что любая первообразная Φ(x) непрерывной на сегменте [a,b] функции f(x) имеет вид 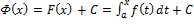 , где C - некоторая постоянная.Полагая в
, где C - некоторая постоянная.Полагая в 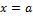 , а затем
, а затем 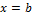 , найдем
, найдем 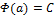 ,
, 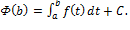 Из этих равенств вытекает соотношение
Из этих равенств вытекает соотношение 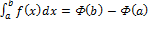 , называемое формулой Ньютона-Лейбница, для вычисления определенных интегралов от функций f(x), для которых известны первообразные на сегменте [a,b].
, называемое формулой Ньютона-Лейбница, для вычисления определенных интегралов от функций f(x), для которых известны первообразные на сегменте [a,b].
Итак, для вычисления определенного интеграла от непрерывной функции f(x) нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.Из формулы 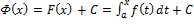 следует связь между определенным и неопределенным интегралами
следует связь между определенным и неопределенным интегралами 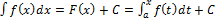
19 Интегрирования по частям и замена переменной в определенном интеграле
Метод замены переменной
Пусть функция у = f(х) непрерывна на отрезке [a, b], а функция x=φ(t), определена на отрезке [α, β] и имеют на нем непрерывную производную, причем φ (α) = а, φ (β) = b и для всех 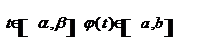 . Тогда
. Тогда
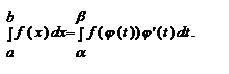
Метод интегрирования по частям
Если функции u = u(x), v = v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула
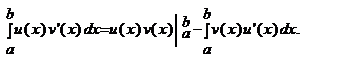 Доказательство.
Доказательство.
Поскольку функция u(x)v(x) – первообразная для функции u’(x)v(x) + u(x)v’(x), то
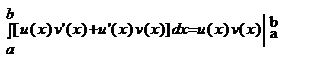
откуда и следует формула 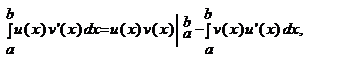 которую можно записать в виде
которую можно записать в виде
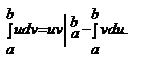
Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то 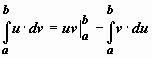 .
.
Необходимое условие интегрируемости.
Если функция интегрируема на отрезке, то она ограничена на нем.
Необходимое и дост. усл. интегрируемости.
Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0
20. Понятие площади плоской фигуры, объем тела. Вычисление объема площади плоских фигур и объемов тел вращения
площадь S криволинейной трапеции abAB, ограниченной кривой y=f(x), f(x) 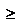 0
0
| y |
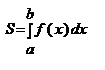
| x |
| b |
| а |
| y=f(x) |
| B |
| A |
| y |
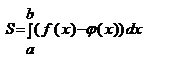
| x |
| A |
| B |
| y=φ(x) |
| C |
| y=f(x) |
| D |
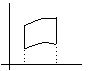
Объем тела, образованного вращением кривой y = f(x), ограниченной прямыми х = а, x = b при a<x<b вокруг оси Ох, вычисляется по формуле:
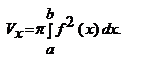
Объем тела, образованного вашей кривой у = φ(у), ограниченной прямымиy = c, y = d при c<y<d вокруг оси Oy, вычисляется по формуле:
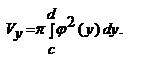
Центральный угол — это угол, образованный двумя радиусами. Длина дуги, описываемой концом радиуса, пропорциональна величине соответствующего центрального угла. Центральный угол дуги измеряется градусами. Для измерения градусами - целая окружность имеет 360°. Длина дуги
p=2π r n\360=π r n\180
Определение 3. Тело вращения – это тело, полученное вращением плоской фигуры  вокруг оси, не пересекающей фигуру и лежащей с ней в одной плоскости.
вокруг оси, не пересекающей фигуру и лежащей с ней в одной плоскости.
Ось вращения может и пересекать фигуру, если это ось симметрии фигуры.
Теорема 2. Пусть криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции 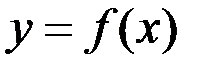 , осью
, осью 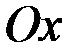 и отрезками прямых
и отрезками прямых 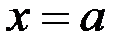 и
и 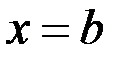
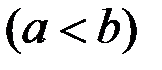 вращается вокруг оси
вращается вокруг оси 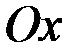 . Тогда объём получающегося тела вращения можно вычислить по формуле
. Тогда объём получающегося тела вращения можно вычислить по формуле
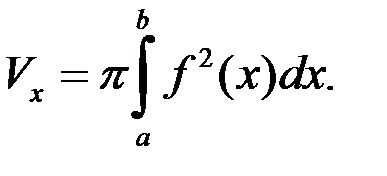 (2)
(2)
Доказательство. Для такого тела сечение с абсциссой 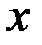 – это круг радиуса
– это круг радиуса 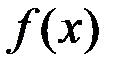 , значит
, значит 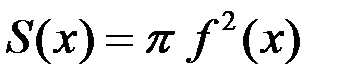 и формула (1) даёт требуемый результат.
и формула (1) даёт требуемый результат.
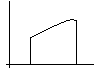
Если фигура ограничена графиками двух непрерывных функций 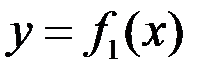 и
и 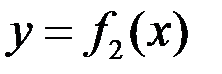 , и отрезками прямых
, и отрезками прямых 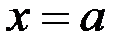 и
и 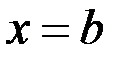 , причём
, причём 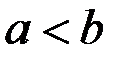 и
и 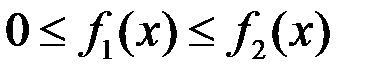 , то при вращении вокруг оси абсцисс получим тело, объём которого
, то при вращении вокруг оси абсцисс получим тело, объём которого
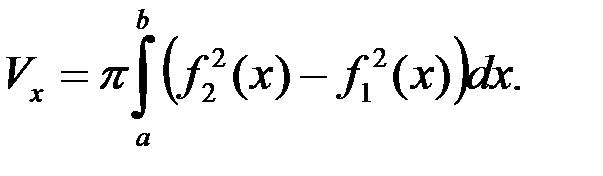
Определение 1. Поверхность вращения – это поверхность, которая получается при вращении плоской линии 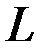 вокруг оси, лежащей в её плоскости и не пересекающей её.
вокруг оси, лежащей в её плоскости и не пересекающей её.
Ось вращения может и пересекать линию, если это ось симметрии линии. В этом случае рассматривают лишь «половину» линии.
Впишем в кривую 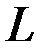 произвольную ломанную и обозначим
произвольную ломанную и обозначим 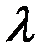 длину наибольшего её звена. При вращении этой ломанной вокруг оси мы получим поверхность
длину наибольшего её звена. При вращении этой ломанной вокруг оси мы получим поверхность 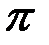 , составленную из боковых поверхностей усеченных конусов. Обозначим площадь этой поверхности
, составленную из боковых поверхностей усеченных конусов. Обозначим площадь этой поверхности 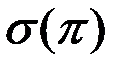 .
.
Определение 2. Конечный предел 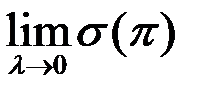 называют площадью поверхности вращения.
называют площадью поверхности вращения.
Можно показать, что если линия 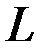 имеет длину, то поверхность, полученная её вращением, имеет площадь.
имеет длину, то поверхность, полученная её вращением, имеет площадь.
II Общая формула
Линия 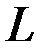 , вращением которой вокруг оси абсцисс получена поверхность, может быть задана одним из следующих способов:
, вращением которой вокруг оси абсцисс получена поверхность, может быть задана одним из следующих способов:
1) 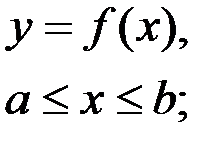 2)
2) 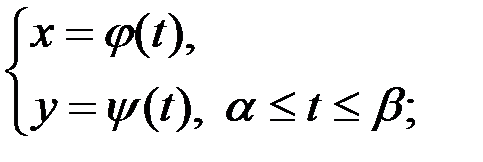 3)
3) 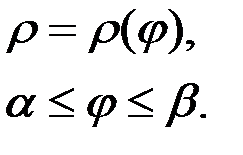
Теорема. Если функции, определяющие линию, непрерывны вместе со своими производными, то площадь поверхности вращения (вокруг оси 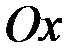 ) определяется формулой:
) определяется формулой:
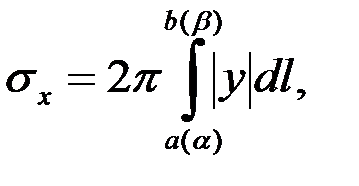 (1)
(1)
где 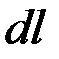 – подынтегральное выражение, фигурирующее в соответствующей формуле для длины дуги.
– подынтегральное выражение, фигурирующее в соответствующей формуле для длины дуги.
Идея доказательства. Пусть концы 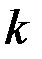 -го звена ломанной имеют координаты
-го звена ломанной имеют координаты 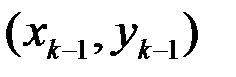 и
и 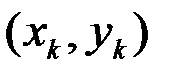 . Это звено при вращении вокруг оси
. Это звено при вращении вокруг оси 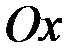 опишет боковую поверхность усеченного конуса с радиусами оснований
опишет боковую поверхность усеченного конуса с радиусами оснований 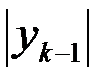 и
и 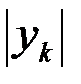 и образующей
и образующей 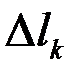 (длина
(длина 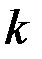 -го звена). Для площади такой поверхности известна формула
-го звена). Для площади такой поверхности известна формула
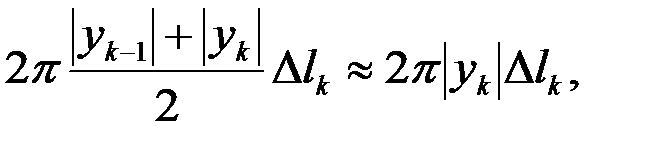
Вся ломанная даст поверхность с площадью
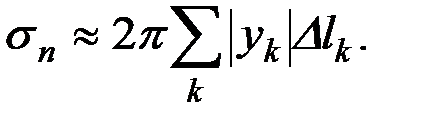
Если, например, имеющаяся кривая – это график функции 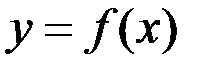 , тогда
, тогда 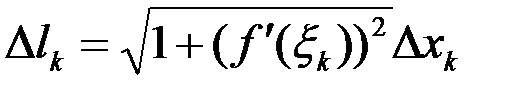 (см. §3, II). Также, заменяя
(см. §3, II). Также, заменяя 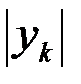 на
на 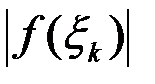 получим
получим
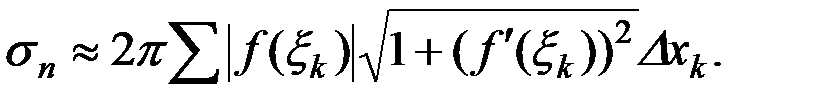
В этой сумме нетрудно увидеть интегральную сумму, которая в пределе даст интеграл из (1).
21. Спрямляемые дуги. Достаточное условие справляемости дуг, вывод формулы для исчисления ее длины
. В приложениях математики возникает потребность в вычислении длин дуг произвольных кривых. Но, чтобы вычислить длину произвольной кривой, надо быть уверенным в том, что рассматриваемая кривая имеет конечную длину.
В средней школе длиной окружности называют предел последовательности периметров вписанных в окружность правильных многоугольников ( при неограниченном удвоении числа сторон). Однако это определение неприменимо к произвольным кривым.
Дадим общее определение понятия длины кривой. Пусть задана жорданова кривая Г1:
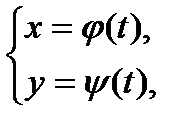 (1)
(1)
a 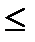 t
t 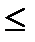 в.
в.
Напомним, что функции 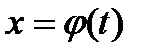 и
и 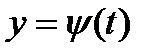 непрерывны на отрезке. Разобьём отрезок [а;в] на части числами
непрерывны на отрезке. Разобьём отрезок [а;в] на части числами
t0, t1,…, tn: a = t0 < t1 < … < tn = в.
Каждому числу t соответствует точка Мк ( 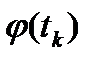 ,
, 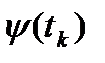 ) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l(ɣ).
) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l(ɣ).
Определение. Жорданова кривая (1) называется спрямляемой (имеющей длину), если множество 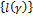 длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества
длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества 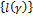 называется длиной кривой Γ и обозначается
называется длиной кривой Γ и обозначается 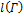 :
:
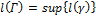 . (2)
. (2)
Докажем, что длина спрямляемой кривой обладает свойством аддитивности.
Пусть жорданова кривая Γ разбита на кривые 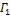 и
и 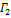 . Если эти кривые спрямляемы, то кривая Γ спрямляема, причем
. Если эти кривые спрямляемы, то кривая Γ спрямляема, причем 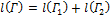 .
.
В самом деле, пусть γ – любая ломаная, вписанная в кривую Γ, и пусть М – точка, разбивающая Γ на 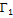 и
и 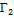 . Добавляя эту точку к вершинам ломаной γ, получим ломаную
. Добавляя эту точку к вершинам ломаной γ, получим ломаную 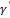 , длина которой не меньше длины ломаной γ,
, длина которой не меньше длины ломаной γ, 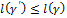 . Но ломаная
. Но ломаная 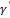 состоит из двух частей
состоит из двух частей 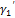 и
и 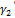 , вписанных соответственно в кривые
, вписанных соответственно в кривые 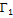 и
и 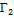 , причем
, причем 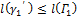 и
и 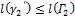 .
.
Поэтому
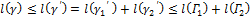 .
.
Это неравенство показывает, что число 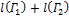 является одной из верхних границ для множества
является одной из верхних границ для множества 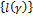 длин ломаных, вписанных в кривую Γ. Но для любого
длин ломаных, вписанных в кривую Γ. Но для любого 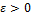 найдутся ломаные
найдутся ломаные 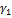 и
и 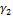 , вписанные в
, вписанные в 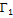 и
и 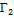 , такие, что
, такие, что
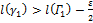 и
и 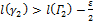 .
.
Объединяя 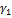 и
и 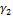 , получаем ломаную γ, вписанную в Γ и такую, что
, получаем ломаную γ, вписанную в Γ и такую, что
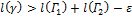 .
.
А это и значит, что 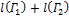 - точная верхняя граница множества
- точная верхняя граница множества 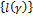 , т.е.
, т.е.
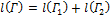 .
.
