Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:
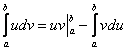
Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения 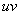 и, после того, как мы возьмем интеграл
и, после того, как мы возьмем интеграл 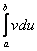 .
.
Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.
Пример 8
Вычислить определенный интеграл
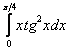
Решаем.
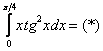
Интегрируем по частям:

У кого возникли трудности с интегралом 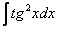 , загляните на урок Интегралы от тригонометрических функций, там он подробно разобран.
, загляните на урок Интегралы от тригонометрических функций, там он подробно разобран.
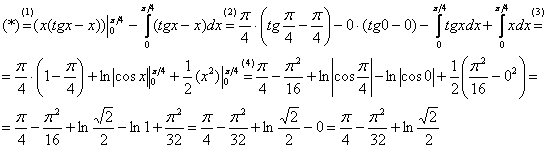
(1) Записываем решение в соответствии с формулой интегрирования по частям.
(2) Для произведения 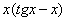 применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!
применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!
(3) Берем два оставшихся интеграла. Интеграл 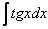 также разобран на уроке Интегралы от тригонометрических функций
также разобран на уроке Интегралы от тригонометрических функций
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.
Если честно, я недолюбливаю формулу 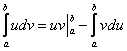 и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.
и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.
Вычислить определенный интеграл
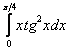
На первом этапе я нахожу неопределенный интеграл:
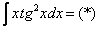
Интегрируем по частям:
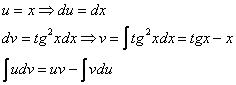
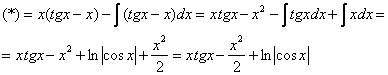
Первообразная функция найдена. Константу  в данном случае добавлять не имеет смысла.
в данном случае добавлять не имеет смысла.
В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования
На втором этапе я провожу проверку (обычно на черновике).
Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:
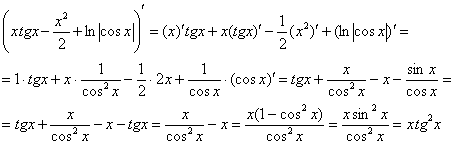
Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.
Третий этап – применение формулы Ньютона-Лейбница:
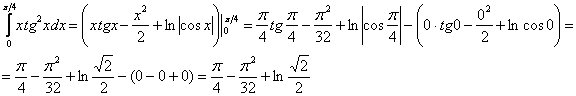
И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле 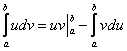 (первым способом), то стопудово где-нибудь допустит ошибку.
(первым способом), то стопудово где-нибудь допустит ошибку.
Рассмотренный алгоритм решения можно применить для любого определенного интеграла.
Уважаемый студент, распечатай и сохрани:
