Замена переменной в определенном интеграле

Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле.

В этом параграфе нет ничего страшного или сложного. Новизна состоит в вопросе, как поменять пределы интегрирования при замене.

В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.

Пример 5

Вычислить определенный интеграл

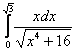
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 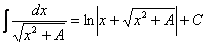. Но есть одна неувязочка, в табличном интеграле под корнем 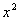, а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

Сначала готовим наш интеграл к замене:

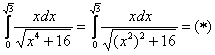
Из вышеуказанных соображений совершенно естественно напрашивается замена: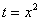
Таким образом, в знаменателе будет всё хорошо: .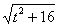
Выясняем, во что превратится оставшаяся часть 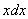подынтегрального выражения, для этого находим дифференциал :

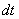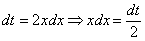
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.

Находим новые пределы интегрирования.

Это достаточно просто. Смотрим на нашу замену 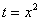и старые пределы интегрирования , .

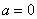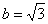Сначала подставляем в выражение замены 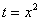нижний предел интегрирования, то есть, ноль:

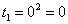
Потом подставляем в выражение замены 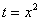верхний предел интегрирования, то есть, корень из трёх:

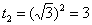
Готово. И всего-то лишь…

Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.

(2) Это простейший табличный интеграл, интегрируем по таблице. Константу 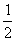лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования 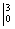– это подготовка для применения формулы Ньютона-Лейбница.

(3) Используем формулу Ньютона-Лейбница .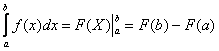

Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.

Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.

А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.

Пример 6

Вычислить определенный интеграл

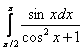
Пример 7

Вычислить определенный интеграл

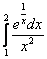
Это примеры для самостоятельного решения. Решения и ответы в конце урока.

И в заключение параграфа пара важных моментов, разбор которых появился благодаря посетителям сайта. Первый из них касается правомерности замены. В некоторых случаях её проводить нельзя! Так, Пример 6, казалось бы, разрешим с помощью универсальной тригонометрической подстановки 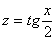, однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» 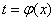должна быть непрерывна во всех точках отрезка 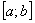интегрирования.

В другом электронном письме поступил следующий вопрос: «А нужно ли менять пределы интегрирования, когда мы подводим функцию под знак дифференциала?». Сначала я хотел «отмахнуться от ерунды» и автоматически ответить «конечно, нет», но затем задумался о причине появления такого вопроса и вдруг обнаружил, что информации-тоне хватает. А ведь она, пусть и очевидна, но очень важнА:

Если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно! Почему? Потому что в этом случае нет фактического перехода к новой переменной. Например:

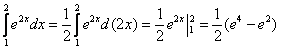
И здесь подведение гораздо удобнее академичной замены 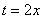с последующей «росписью» новых пределов интегрирования. Таким образом, если определённый интеграл не очень сложен, то всегда старайтесь подвести функцию под знак дифференциала! Это быстрее, это компактнее, и это обыденно – в чём вы убедитесь ещё десятки раз!

Большое спасибо за ваши письма!