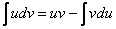Метод замены переменной в неопределенном интеграле

Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.

Пример 5

Найти неопределенный интеграл.

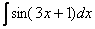
В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула 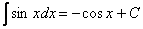, и всё дело хотелось бы свести к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается: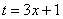
Вторая по популярности буква для замены – это буква .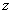
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак:
Но при замене у нас остаётся 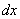! Наверное, многие догадались, что если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву , и дифференциалу 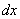там совсем не место.
Следует логичный вывод, что 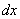нужно превратить в некоторое выражение, которое зависит только от.

Действие следующее. После того, как мы подобрали замену, в данном примере, 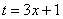, нам нужно найти дифференциал 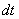. С дифференциалами, думаю, дружба уже у всех налажена.

Так как 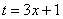, то

После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко:
Теперь по правилам пропорции выражаем нужный нам :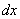

В итоге: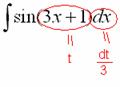
Таким образом:

А это уже самый что ни на есть табличный интеграл 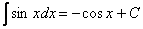(таблица интегралов, естественно, справедлива и для переменной ).

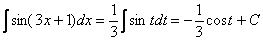
В заключении осталось провести обратную замену. Вспоминаем, что .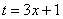

Готово.

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

“

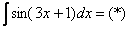
Проведем замену: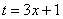

“

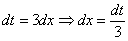
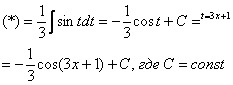
Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Также всем рекомендую использовать математический знак 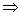вместо фразы «из этого следует это». И коротко, и удобно.

При оформлении примера в тетради надстрочную пометку 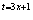обратной замены лучше выполнять простым карандашом.

Внимание! В следующих примерах нахождение дифференциала 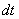расписываться подробно не будет.

А теперь самое время вспомнить первый способ решения:

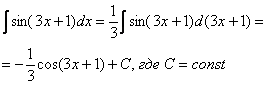
В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче.

Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.

Пример 6

Найти неопределенный интеграл.

Проведем замену: 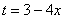(другую замену здесь трудно придумать)

Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:

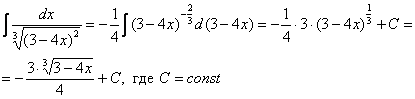
Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.

Пример 7

Найти неопределенный интеграл. Выполнить проверку.

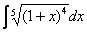
Это пример для самостоятельного решения. Ответ в конце урока.

Пример 8

Найти неопределенный интеграл.

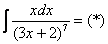
Замена:
Осталось выяснить, во что превратится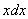

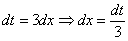
Хорошо, 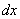мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: 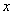мы выразим из той же замены !

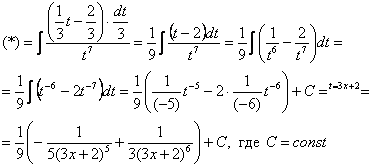
Готово.

Пример 9

Найти неопределенный интеграл.

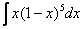
Это пример для самостоятельного решения. Ответ в конце урока.

Пример 10

Найти неопределенный интеграл.

Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.

Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция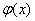 и её производная : 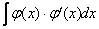(функции 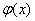, могут быть и не в произведении)

В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.

В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель 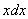превратится во что-нибудь хорошее.

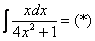
Замена: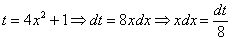

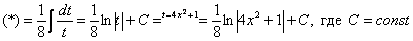
Кстати, здесь не так сложно подвести функцию под знак дифференциала:

Следует отметить, что для дробей вроде 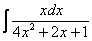, такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.

Вот еще пара типовых примеров для самостоятельного решения из той же оперы:

Пример 11

Найти неопределенный интеграл.

Пример 12

Найти неопределенный интеграл.

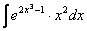
Решения в конце урока.

Пример 13

Найти неопределенный интеграл.

Смотрим в таблицу производных и находим наш арккосинус: . У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.

Общее правило:
За обозначаем саму функцию (а не её производную).

В данном случае: 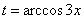. Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения .

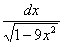В этом примере нахождение 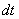я распишу подробно поскольку – сложная функция.

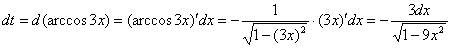
Или короче:
По правилу пропорции выражаем нужный нам остаток: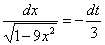

Таким образом:

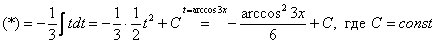
Вот здесь подвести функцию под знак дифференциала уже не так-то просто.

Пример 14

Найти неопределенный интеграл.

Пример для самостоятельного решения. Ответ совсем близко.

Внимательные читатели заметили, что я рассмотрел мало примеров с тригонометрическими функциями. И это не случайно, поскольку под интегралы от тригонометрических функций отведён отдельный урок. Более того, на указанном уроке даны некоторые полезные ориентиры для замены переменной, что особенно актуально для чайников, которым не всегда и не сразу понятно, какую именно замену нужно проводить в том или ином интеграле. Также некоторые типы замен можно посмотреть в статье Определенный интеграл. Примеры решений.

Более опытные студенты могут ознакомиться с типовой заменой в интегралах с иррациональными функциями. Замена при интегрировании корней является специфической, и её техника выполнения отличается от той, которую мы рассмотрели на этом уроке.

Желаю успехов!

Пример 3:Решение:

Пример 4:Решение:

Пример 7:Решение:

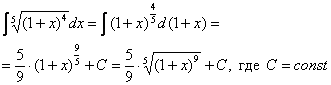
Пример 9:Решение:

Замена:

Пример 11:Решение:

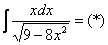
Проведем замену:

Пример 12:Решение:

Проведем замену:

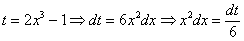
Пример 14:Решение:

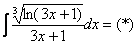
Проведем замену:

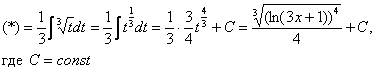
Интегрирование по частям. Примеры решений

И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статьюНеопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статьюМетод замены переменной в неопределенном интеграле)либо интеграл как раз на метод интегрирования по частям.

Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.

Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.

Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы: . Зато есть такая: 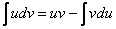– формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).

И сразу список в студию. По частям берутся интегралы следующих видов:

1) 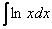, , 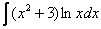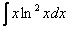– логарифм, логарифм, умноженный на какой-нибудь многочлен.

2) 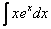, 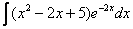– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 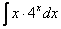– показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.

3) 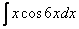, , 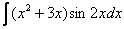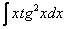– тригонометрические функции, умноженные на какой-нибудь многочлен.

4) 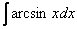, 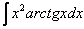– обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.

Интегралы от логарифмов

Пример 1

Найти неопределенный интеграл.

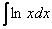
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:

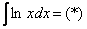
Прерываем решение на промежуточные объяснения.

Используем формулу интегрирования по частям: