Аннуитет и перпетуитет

Часто в сберегательных схемах, инвестиционном проекте или схеме возврата кре­дита будущие денежные поступления или выплаты (т.е. положительные или отрица­тельные денежные потоки) остаются неизменными из года в год. Такого рода ряд по­стоянных поступлений или выплат денег называется аннуитетом,илирентой (annuity). Ряд платежей по рассрочке или ипотеч­ному договору также называется аннуитетом. Если денежные платежи начинаются «немедленно, как это присуще сберегательному плану или аренде, такой договор назы­вается срочнымилинемедленным аннуитетом (immediate annuity) расчеты ведутся на условиях prenumerando «пренумерандо». Если денежный по­ток начинается в конце текущего периода, а не немедленно, такой договор называется обычным аннуитетом (ordinary annuity) и расчеты ведутся на условиях postnumerando «постнумерандо». Ипотека является примером обычного аннуи­тета.

ПРИМЕР

В конце каждого года в течение 5 лет клиент вносит в банк 100 тысяч рублей. По каждому взносу в конце года начисляются сложные проценты по ставке 10% годовых. Тогда к концу периода накопления величина накопленной суммы составит:

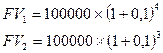
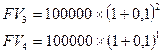
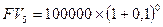, т.е.

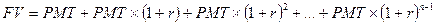или

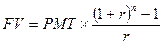[3]

ЗАДАЧИ для третьей формулы

Ежегодно в конце года в течение 4 лет на специальный счет поступают 50 д.е. Определите будущую стоимость, если ежегодно в конце года осуществляется начисление сложных процентов по ставке 10% годовых.

Решение:

n=4, PMT=50, r=0,1

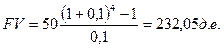
Фактор фонда замещения отвечает на вопрос: Какой должен быть ежегодный платеж для создания необходимого фонда, если известны FV, %, n.

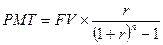[3а]

ЗАДАЧИ для формулы 3 и 3а:

Иван Иванович, которому сейчас 55 лет решил накопить на пенсию. Он планирует раз в год в начале периода вкладывать $2000. Сколько он накопит при ставке доходности 5%?

Сколько ему надо вкладывать, чтобы накопить $15000?

Решение:

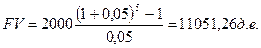
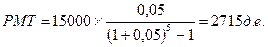
Если Иван Иванович из предыдущей задачи хочет брать из накоплений по $500 ежегодно, сколько ему необходимо вложить, чтобы исчерпать сбережения в течение 5 лет? Ответ на этот вопрос дает расчет «взноса на амортизацию единицы.

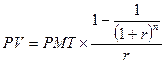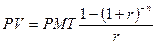или [4]

Решение:

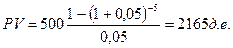
ЗАДАЧИ для четвертой формулы

Какова текущая стоимость ипотечного кредита, предусматривающего выплату 100 000 рублей в конце каждого месяца на протяжении одного года? Ставка дисконта 20%.

Решение:

PMT=100000, n=1, m=12, r=0,2

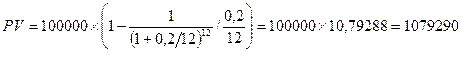
Формулы для расчета на условиях prenumerando «пренумерандо»:

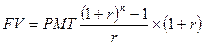[5]

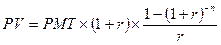[6]

Особым типом аннуитета является бессрочный аннуитет, или пожизненная рента (перпетуитет) (perpetuity). Пожизненная рента — это ряд денежных выплат, который продолжается вечно. Классическим примером могут служить облигации «консоль», выпушенные британским правительством в девятнадцатом веке, процент по номиналу которых вы­плачивался каждый год, но которые не имели срока погашения. Другим примером и, возможно, более актуальным может служить привилегированная акция, по которой дивиденды выплачиваются по итогам каждого периода (обычно поквартально) и которая не имеет обусловленного срока выкупа.

Неудобной особенностью любой пожизненной ренты является то, что вы не можете рассчитать будущую стоимость выплат по ней, потому что она бесконечна. Несмот­ря на это, она имеет вполне определенную приведенную стоимость. На первый взгляд может показаться парадоксальным, что серия денежных выплат, которая длится вечно имеет в настоящее время определенную стоимость. Давайте рассмотрим бессрочный поток денежных выплат в 100 долл. в год. Если процентная ставка составляет 10% годовых, то какова стоимость этой пожизненной ренты сегодня?

Ответ: 1000 долл. Для того чтобы понять, как мы получили этот результат, подумайте, сколько денег вы должны были бы положить на банковский счет, по которому выплачивается 10% годовых с тем, чтобы снимать по 100 долл. каждый год до скончания века. Если бы вы положили на счет 1000 долл., то к концу первого года у вас на счете было бы 1100 долл. Вы могли бы снять со счета 100 долл., оставив 1000 долл. на второй год. Совершенно ясно, что если процентная ставка оставалась бы на уровне 10% годовых и вы располагали бы эликсиром бессмертия, вы могли бы продолжать такую практику вечно.

Если обобщить сказанное, формула для расчета приведенной стоимости пожиз­ненной ренты выглядит следующим образом:

PV пожизненной ренты = PMT / r [7]

где PMT – периодические платежи, r – процентная ставка, выраженная десятичной дробью. Это приведенная стоимость обычного аннуитета с n = ∞.

ЗАДАЧИ для седьмой формулы

Даниил хочет учредить благотворительный счет, который постоянно выплачивать пожертвования в $1000 лучшему учителю в школе, в которой он учился. Сколько денег нужно вложить для этого сегодня, если по счету начисляется 7% годовых ежегодно.

Решение:

1000/0,07=14 286

Инфляция и приведенная стоимость.

Различаются реальные и номинальные цены, различаются реальные и номинальные процентные ставки. Номинальные процентные ставки по облигациям представляют собой обещанную заемщиком сумму, которую Вы получите за ссуженные Вами деньги. Реальная ставка доходности – это заработанная кредитором номинальная процентная ставка, откорректированная с учетом изменения покупательной способности денег. Например, если начисленная номинальная процентная ставка составляет 8% годовых, а уровень инфляции также равен 8%, то реальная ставка доходности будет нулевой.

Какова же будет реальная процентная ставка доходности, если номинальная составляет 8% в год, а уровень инфляции, который изменяется пропорционально изменению индекса потребительских цен, - 5% в год? На чисто интуитивном уровне следовало бы предположить, что реальная ставка доходности представляет собой не что иное, как разницу между номинальной процентной ставкой и уровнем инфляции, т.е. для нашего примера этот показатель будет 3% в год. В принципе, это верно, но с некоторыми оговорками.

Номинальная процентная ставка – Уровень инфляции

Реальная процентная ставка = ----------------------------------------- ------------- [8]

1 + Уровень инфляции

0,08 – 0,05

Реальная процентная ставка = 1,05 = 0,02857 = 2,857%

Во многих финансовых задачах, где рассчитывается приведенная стоимость, бу­дущая сумма не фиксируется. Предположим, вы планируете купить машину через четыре года и хотите сейчас отложить достаточно денег для того, чтобы заплатить за нее. Машина, о покупке которой вы подумываете, стоит, скажем, 10000 долл., а процентная ставка, под которую вы можете поместить свои деньги в банк, состав­ляет 8% годовых..

Пытаясь рассчитать, какую сумму вам необходимо вложить сейчас, вполне естественно следующим образом рассчитывать приведенную стоимость 10000 долл., которые будут получены через четыре года при ставке 8%:

PV = 10000 долл. /1,08⁴=7350 долл.

Вы вполне можете прийти к заключению, что сейчас достаточно вложить в банк 7350 долл., чтобы этих денег хватило заплатить через четыре года за машину.

Но это было бы ошибкой. Если машина, которую вы хотите купить, стоит сейчас 10000 долл., почти наверняка через четыре года она будет стоить больше. Насколько больше? Это зависит от уровня инфляции. Если цены на машины растут на 5% в год, то через четыре года машина будет стоить долл.10000 х 1,05⁴, или 12155 долл.

Есть два равнозначных способа учета инфляции для таких ситуаций. Первый способ заключается в том, чтобы рассчитать приведенную стоимость, используя реальную дисконтную ставку.

Используя реальную ставку для расчета текущей стоимости 10000 долл., мы найдем:

PV = 10000 долл./1,02857⁴ = 8934 долл.

Второй способ состоит в том, чтобы рассчитать приведенную стоимость 12155 долл., — номинальной будущей суммы, используя номинальную дисконтную ставку 8% годовых:

PV = 12155 долл./1,08⁴ = 8934 долл.

Тем или иным способом мы получаем тот же результат: вы должны вложить 8934 долл. сейчас для того, чтобы покрыть возросшую в связи с инфляцией цену машины через четыре года. Причина, по которой мы в первый раз ошибочно подсчита­ли необходимую для вклада сумму (всего лишь 7350 долл.), заключается в том, что мы дисконтировали реальную будущую сумму 10000 долл. по номинальной дисконтной ставке в 8% годовых.

«При оценке альтернативных вариантов инвестиций никогда не сравнивайте реальную ставку доходности с самой высокой номинальной доходностью по альтернативному виду инвестиций».

«Никогда не используйте номинальную процентную ставку при дисконтировании реальных денежных потоков или реальную процентную ставку при дисконтировании номинальных денежных потоков».

Домашнее задание:

1. Иван Иванович отправился на пенсию. Он накопил на индивидуальном пенсионном счете 1млн долларов. Если он хочет изымать со своего счета одну и ту же сумму ежемесячно таким образом, чтобы довести свой счет до нуля через 20 лет. При этом он будет получать 7% годовых дохода на свои деньги на счете. Какова может быть сумма ежемесячных изъятий со счета?

2. Менеджеры компании хотят подобрать подходящую структуру капитала. Если фирма продает 5 млн. вечных облигаций с годовым купонным платежем 8% по их номинальной стоимости $1, то какова будет современная ценность налоговой льготы, если ставка корпоративного налога 20%.

3. Какое влияние оказало бы на Ваш постоянный годовой доход наследство 1 млн. долларов, которые Вы надеетесь получить к пенсионному возрасту?

4. У Вас есть $1000 . Выберите привлекательный вариант инвестиций на 3 года.

1) положить в банк под 6% годовых с ежеквартальным начислением процентов.

2) приобрести ценные бумаги, где прогноз роста индекса цен составляет в 1-й год – 10%, 2-ой- 5%, 3-й – 4% с реинвестированием раз в год.

3) Ваше предложение по существующим активам на рынке.