Критерии принятия решений в условиях полной неопределенности

Если известны законы распределения доходности финансовой операции развивающейся в той или иной экономической ситуации, или хотя бы вероятности различных возможных исходов данной финансовой операции, то инвестор при принятии решения может руководствоваться вероятностными показателями, описанными в п. 3.2.

Но ситуация может быть полностью неопределенной, то есть не известны ни вероятности различных исходов финансовой операции ни, тем более, закон распределения доходности финансовой операции. В данных условиях полной неопределенности инвестор или лицо принимающее решение может только предположить возможные варианты развития экономической ситуации при ее совершении.

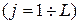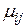Предположим, что число возможных ситуаций конечно и равно L. В каждой предполагаемой j-той ситуации лицо принимающее решение (ЛПР) – инвестор может принять N финансовых решений. В случае принятия i-того финансового решения могут быть рассчитаны доходности финансовой операции при принятии i-того решения в j-той экономической ситуации. Эти возможные значения доходности 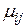образуют матрицу доходностей.

	j i				¼	L	(3.28)
					¼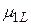
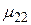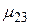					¼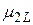
M =				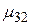	¼
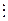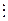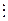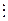	N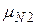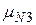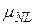

Предположим, инвестором предполагается три возможных варианта развития ситуации L = 3. В каждой из возможных ситуаций ЛПР может принять по четыре решения N = 4. Анализ развития финансовой операции при принятии i-того решения в j-той экономической ситуации позволил определить все элементы матрицы доходностей.

(3.29)

Как было отмечено в п. 3.2 принимаемое решение в условиях неопределенности зависит от склонности ЛПР к риску. Поясним подходы к определению риска в данной ситуации полной неопределенности.

Определим величины риска, которые соответствуют принятию i-того решения в j-той ситуации - 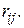Если бы ЛПР однозначно знало ситуацию, которая реально сложится при развитии финансовой операции, то выбрало бы решение, обеспечивающее максимальную доходность. Если реальная ситуация соответствовала бы j-той, то было бы принято решение обеспечивающее максимальную доходность:

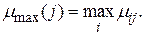(3.30)

При принятии любого i-того решения в j-той ситуации ЛПР рискует получить доходность не 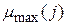, а только При таком определении риски 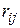логично определять разностью:

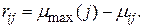(3.31)

Элементы 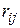, рассчитываемые по формуле (3.31), образуют матрицу рисков. Составим матрицу рисков, соответствующую матрице доходностей (3.29). Для максимальных доходностей 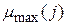в соответствии с (3.30) получим

В соответствии с (3.31) матрица рисков будет иметь вид:

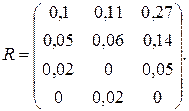(3.32)

По матрице доходностей (3.27) могут быть приняты финансовые решения, являющиеся оптимальными по тому или иному критерию. При принятии финансовых решений используют следующие критерии.

Правило Вальда

При принятии решения в соответствии с данным правилом предполагают, что будет иметь место самая неблагоприятная ситуация. В соответствии с данным предположением правило Вальда называют также правилом крайнего пессимизма. Самая неблагоприятная ситуация характеризуется самой малой доходностью:

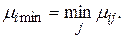(3.33)

В соответствии с матрицей доходности (3.29) по правилу (3.33) находим:

Правило Вальда рекомендует принять решение с наибольшим значением то есть

(3.34)

В соответствии с правилом (3.34) оптимальным по правилу Вальда будет третье решение 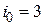с доходностью:

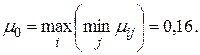
3.4.2. Правило "розового оптимизма"

В соответствии с этим правилом предполагается, что будет действовать самая благоприятная ситуация, которая при любом i-том решении обеспечит максимальную доходность:

(3.35)

В соответствии с матрицей доходности (3.29) по правилу (3.35) находим:

Оптимальным решением по правилу "розового оптимизма" является решение , обеспечивающее максимальную доходность из всех

(3.36)

Из приведенных значений 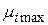видно, что по правилу "розового оптимизма" оптимальным решением будет четвертое решение с доходностью:

Правило Гурвица

По правилу Гурвица оптимальным считается решение , которое обеспечивает максимум взвешенной суммы доходностей пессимистического (3.34) и оптимистического (3.36) подходов:

(3.37)

где 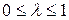- весовой коэффициент, значение которого выбирается лицом, принимающим решение из субъективных соображений.

При правило Гурвица совпадает с правилом Вальда, а при - с правилом "розового оптимизма".

Вычислим значения:

(3.38)

для двух значений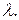

При 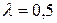получим следующие значения :

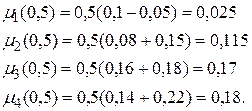
В соответствии с правилом (3.37) видно, что оптимальным является четвертое решение

При 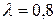получим следующие значения :

Из вычисленных значений видно, что при 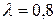оптимальным является третье решение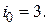

Правило Сэвиджа

Правило Сэвиджа называют также правилом минимального риска. При применении этого правила анализируется матрица рисков и предполагается, что будет действовать ситуация максимального риска:

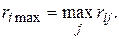(3.39)

В соответствии с правилом Сэвиджа оптимальным считается решение 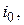при котором обеспечивается минимальное значение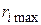

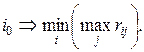(3.40)

По приведенным выше значениям элементов матрицы (3.32) для 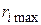в соответствии с (3.39) получим:

Из вышеперечисленных значений 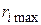и правила (3.40) следует, что оптимальным является четвертое решение при минимальном значении риска

Контрольные вопросы и задания

1. Привести перечень и дать характеристику факторов, от которых зависит доходность финансовых операций в условиях неопределенности.

2. Записать математическое выражение для совместной плотности вероятностей доходностей двух финансовых операций. Пояснить смысл величин .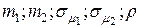

3. Определение математического ожидания суммарной доходности двух зависимых финансовых операций.

4. Определение математического ожидания и среднеквадратического отклонения суммарной доходности для "n" независимых финансовых операций.

5. Количественная оценка риска финансовой операции. Определение вероятности получения отрицательной доходности финансовой операции. Коэффициент вариации как количественная оценка риска финансовой операции.

6. Две финансовые операции характеризуются следующими значениями доходности и риска 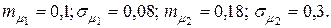Определить для какой финансовой операции риск получения отрицательной доходности будет больше.

7. Количественная оценка риска финансовых операций по показателю (VaR) – стоимости под риском. Пояснить смысл этого показателя.

8. Математическое ожидание и дисперсия доходности финансовой операции соответственно равны 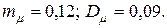определить коэффициент вариации доходности "k_В" и вероятность того, что доходность данной финансовой операции будет больше требуемого значения

9. Диверсификация как метод уменьшения рисков финансовых операций.

10. Организация инвестирует временно свободные средства в две независимые финансовые операции с математическими ожиданиями и среднеквадратическими значениями доходностей 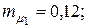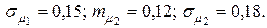Определить значение долей финансирования первой х₁ и второй х₂ финансовых операций, при которых обеспечиваются минимальные риски 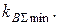Определить суммарную ожидаемую доходность и среднеквадратическое отклонение суммарной доходности при вычисленных значениях долей финансирования х₁ и х₂.

11. Хеджирование как метод уменьшения рисков финансовых операций. Формулы для определения математического ожидания, среднеквадратического отклонения и коэффициента вариации суммарной доходности по двум зависимым финансовым операциям.

12. Определить оптимальные значения стоимостных долей инвестиций в две зависимые финансовые операции х₁ и х₂, обеспечивающие минимум среднеквадратического отклонения суммарной доходности если среднеквадратические отклонения доходностей и коэффициент корреляции по этим операциям равны Для вычисленных значений х₁ и х₂ определить значение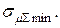

13. Определить оптимальные значения стоимостных долей инвестиций в две зависимые финансовые операции х₁ и х₂, обеспечивающие минимум коэффициента вариации суммарной доходности 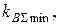если доходности по этим операциям характеризуются следующими значениями 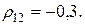Для вычисленных значений х₁ и х₂ определить значения и

14. Определить значения коэффициента корреляции финансовых операций , при котором для оптимальных значениях стоимостных долей инвестирования в эти операции минимальное значение коэффициента вариации суммарной доходности будет не больше 0,5 если коэффициенты вариаций доходностей по этим финансовым операциям имеют значения

15. Изменение внешних условий может привести к трем (L = 3) возможным вариантам развития ситуации. В каждой из этих ситуаций финансовый менеджер может принять (N = 4) четыре управленческих решения. Для данной ситуации экспертным методом определена возможная матрица доходностей:

Составить матрицу рисков соответствующую данной матрице доходностей.

16. По матрице доходностей, приведенной в условии задачи 15, определить оптимальное решение по правилу Вальда.

17. По матрице доходностей, приведенной в условии задачи, определить оптимальное управленческое решение по правилу "розового оптимизма".

18. По матрице доходностей, приведенной в условии задачи 15, определить оптимальное управленческое решение по правилу Гурвица при λ = 0,7.

19. Для матрицы рисков

Определить оптимальное управленческое решение по правилу Сэвиджа.

Портфельный анализ