Метрические пространства (м.п.)
Теория множеств
Множество-совокупность объектов любой природы, называемых элементами множества.
Тавтология- множество синоним совокупности, и так всегда, так как это самое общее исходное понятие математики и внутри этой теории определено быть не может (нелинейное определение материи).
" элементы множества разные, порядок следования несущественен.
C и т.п. – множества, х и т.п. – элементы множества
Множество может быть задано: перечислением элементов
C{х1,х2,х3}, указанием характеризующего свойства Х={х | х-простое}
х Î Х, у Ï Х
Множества:
- конечные
- бесконечные: счётное, несчётное (не более чем счётное)
- пустое = Æ
{Хi} i= 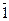 ,n – семейство множеств. Кортеж
,n – семейство множеств. Кортеж
(после отображений)
Примеры
Х=Y 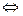 когда они состоят из одних и тех же элементов
когда они состоят из одних и тех же элементов
Х 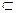 Y
Y 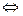 все элементы Х есть элементы Y, но не наоборот, Х – подмножество
все элементы Х есть элементы Y, но не наоборот, Х – подмножество
Каждое множество- подмножество самого себе
Х 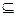 Y Х- подмножество, которое либо Х=Y ,либо Х
Y Х- подмножество, которое либо Х=Y ,либо Х 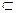 Y
Y
Х= 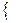 х
х 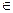 Y
Y 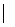 x имеет свойство Р
x имеет свойство Р 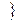
Х=Y 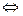 Х
Х 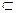 Y и Y
Y и Y 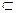 Х
Х
Х 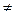 Y
Y
Х 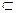 Y
Y 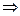 Х
Х 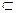 Y и Х
Y и Х 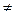 Y(эквивалентность)
Y(эквивалентность)
Операции
1.Пересечение Х 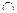 Y, Х
Y, Х 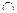 Y=Æ - нет общих элементов
Y=Æ - нет общих элементов
{2,4, 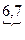 } {1,
} {1, 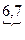 ,10}
,10}
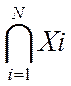
2.Объединение
Х  Y
Y 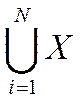
3.Разность
Х \ Y
Дополнение Х к W
Zw(x) = {w 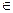 W\x
W\x 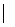 X
X 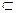 W}
W}
U – универсальное множество Zu(x)=¯|x или 
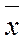
Свойство множеств: ассоциативность, дистрибутивность, коммутативность, идемнотентность (Х 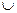 X=X, и Y
X=X, и Y 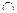 Y=Y), свойства дополнительности (деМорган)
Y=Y), свойства дополнительности (деМорган)
4.Декартово произведение множеств
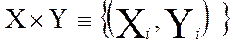
упорядоченные двойники
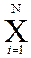
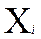
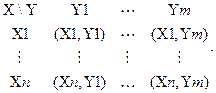

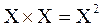 соответственно
соответственно 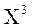 и т.п. степени
и т.п. степени
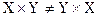
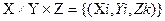
5.Разбиение. Факторизация множеств
Фактор – множества
Множество подмножеств, Х множества Х 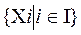
1. 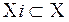
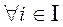
2. 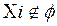
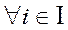
3. 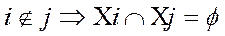 де Морган!!!!
де Морган!!!!
4. 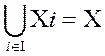
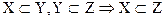
Мощность множества
Отношения на множествах
... Меньше (равно, эквивалентно и т.п.)…..делится на….. :неполные предложения – предикаты обозначающие отношения
Бинарные отношении 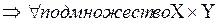
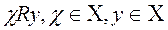
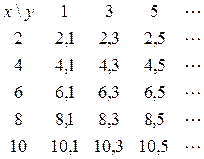
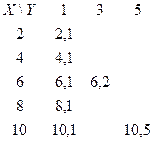
- отношения, делимость без остатка. Отношение может быть пустым.
Тернарное 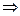 подмножеств
подмножеств 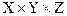 и т.п.(упорядоченные тройки)
и т.п.(упорядоченные тройки)
N – арное, эквивалентность, порядок
Свойства отношений
1.Рефлексивность: 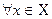 справедливо
справедливо 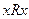
Если не выполняется 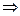 отношение антирефлексивно (равенства рефлексивны, строго больше - антирефлексивны)
отношение антирефлексивно (равенства рефлексивны, строго больше - антирефлексивны)
2.Симметричность: для 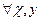
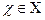 и
и 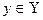 справедливо хRy
справедливо хRy 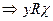
Антисимметричность (х,y) 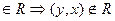 (у равенства строгий порядок)
(у равенства строгий порядок)
Антисимметрические отношения являются и антирефлексивными.
3.Тождественность: xRy и yRx 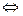 x=y
x=y
(нестрогий порядок).
4.Транзитивность xRy и yRz 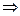 xRz
xRz
параллельность, равенство – транзитивно
перпендикулярность, неравенство – не транзитивно ( 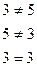 )
)
Обратное отношение: для R <> определить R-1 ,считая, что yR-1 x 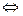 xRy
xRy
x – является делителем y – обратное- y кратно x, x>y R1 y<x
5.Полное
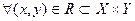
всегда xRy или yR-1x
6.Нулевое отношение – не выполняется ни для одной пары X 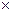 Y
Y
7.Инивереальное - выполняется для 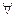 пары.
пары.
8.Дополнительное: 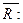
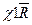
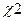 выполняется,
выполняется, 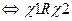 не выполняется.
не выполняется.
Основные виды отношений:
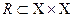 обладающее свойствами рефлексивности, симметричности, транзитивности - отношение эквивалентности. (равенство, подобие, проживание в одном городе)
обладающее свойствами рефлексивности, симметричности, транзитивности - отношение эквивалентности. (равенство, подобие, проживание в одном городе)
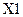 ~Х2
~Х2
Множество 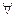 живущих в стране, множество всех живущих в одном городе- класс эквивалентности.
живущих в стране, множество всех живущих в одном городе- класс эквивалентности.
Х1~Х2, 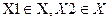
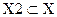
Х2={ 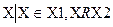 } X2- класс эквивалентности содержащий элемент Х2
} X2- класс эквивалентности содержащий элемент Х2
Отношение эквивалентности разбивает множество на классы эквивалентности.
Класс эквивалентности – непересекающиеся подмножества, фактор- множество.
Низкий порядок ( 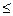 )
)
рефлексивность, транзитивность, антисимметричность.
Порядок
Тождественность, транзитивность.
Строгий порядок (<)
Антисимметричность, транзитивность
Х1 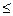 Х2 – Х1 предшествует Х2
Х2 – Х1 предшествует Х2
Х’ 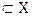 , Х упорядоченное множество
, Х упорядоченное множество
Мажоранта Х’ – элемент Хmax 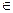 X, следующий за всеми элементами Х’, Xmax
X, следующий за всеми элементами Х’, Xmax 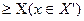 .
.
Мажоранта <> и не принадлежать Х’ .Элемент является мажорантой множества Х’ и 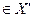 то он называется наибольшим элементом
то он называется наибольшим элементом 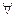 max множества Х’.
max множества Х’.
Мажоранта Хmin 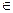 X предшествующий всем элементам Х’, если принадлежит Х’, то наименьший или minХ’.
X предшествующий всем элементам Х’, если принадлежит Х’, то наименьший или minХ’.
Мощность множества
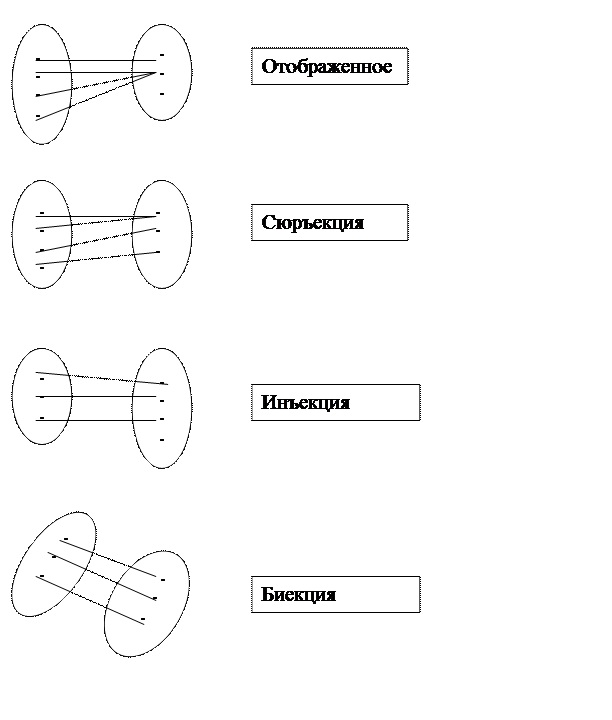
Отображение (закон) инъекция
сюръекция
Х,Y 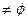 f
f 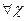

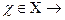 y
y  Y биекция
Y биекция
y=f(x)
Однозначное отображение Х в Y, или функция определенная на Х и принимающая значения на Y
Образом элемента х 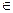 Х называется f(x)
Х называется f(x) 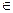 Y
Y
x- идеал f(x) или прообраз f(x)
Образом X’ 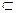 X
X
F(X’)=Uf(x)
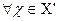
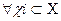
f( 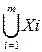 )=
)= 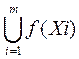 ;
; 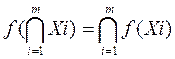 для однозначных
для однозначных
f1*f2 – суперпозиция отображений ассоциативна f1*f2(x)=f1(f2(x))
f2,f3,….=f1*f2….(x)
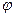 =
= 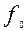 U – замена переменной
U – замена переменной 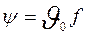 - замена функции
- замена функции
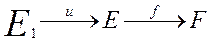
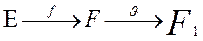
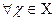
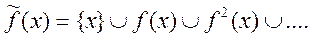


Обратное отображение
f-1(y)={x|y  f(x)2}
f(x)2}
Y 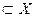 f-1(y)={x|f(x)
f-1(y)={x|f(x) 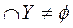 }
}
f-1*f(x)=x- идеал f(x). f-1 не всегда является отображением (всегда только для взаимного отображения)
Множество отображений E в F - FE
(xi)i 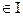 - семейство элементов из Е с индексами из I (или I
- семейство элементов из Е с индексами из I (или I 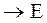 )
)
не путать с {xi} 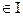 a
a
a*e=a a-1*a=e
e*a=a a*a-1=e
множество семейств (Еi) последовательности частный случай семейств. Упорядоченная пара (х1,х2) ~ (хi)i=1,2
z=f(x,y)- операция
Метрические пространства (м.п.)
Е – м.п. если для его элементов введено понятие расстояния.
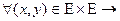 d(x,y)
d(x,y) 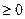
Свойства метрики
1.Симплатрия d(x,y)=d(y,x)
2.Положительность d(x,y)>0 если х 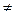 y и d(x,x)=0
y и d(x,x)=0
3.Неравенство треугольника y
|
 d(x,z)
d(x,z) 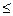 d(x,y)+d(y,z)
d(x,y)+d(y,z) отсюда d(x,z) 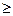 |d(x,y)-d(y,z)|
|d(x,y)-d(y,z)|
|
d(x,xn) 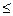 d(x1,x2)+d(x2,x3)+d(xn-1,xn)
d(x1,x2)+d(x2,x3)+d(xn-1,xn)
Дискретная метрика d(x,y)=1 x 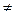 y
y
d(x,x)=0
Многообразие 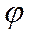
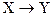
Каждому х 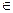 Х ставится в соответствие
Х ставится в соответствие
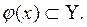 <>
<> 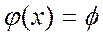 z=f(x,y)-бинарная операция
z=f(x,y)-бинарная операция
отображение-операция n –арная операция
Группа, полугруппа, внутренние и внешние операции.
