Поскольку суммарный NPV в случае четырехкратной реализации проекта А больше (1840,3 тыс руб), то проект А является предпочтительным

Задача 1

Предприятию необходимо привлечь кредит в размере 40 млн. руб. для строительства комбикормового завода. Средне рыночная ставка процента за кредит 20% в год. Коммерческие банки предлагают следующие условия:

	Банк 1	Банк 2	Банк 3
Уровень годовой процентной ставки, %		1год-18 2год-19 3год-21
Срок погашения за кредит	В конце каждого года	В конце каждого года	В конце каждого года
Срок и условия погашения основного долга	В конце кредитного договора	1 год-25 2год-45 3год-30	В начале кредитного договора

Выберите наиболее приемлемые условия привлечения банковского кредита.

Решение:

ГЭ=100% - Сум. [ПР+ОД] / [БС*(1+i)ⁿ] *100

ПР – сумма уплачиваемого процента в конкретном интервале n кредитного периода;

ОД – сумма амортизируемого основного долга в конкретном интервале n кредитного периода;

БС – общая сумма банковской ссуды, привлекаемой предприятием;

i – средняя ставка процента за кредит, сложившаяся на финансовом рынке по аналогичным

кредитным инструментам, выраженная десятичной дробью;

t – общая продолжительность периода, выраженная числом входящих в него интервалов;

n – интервал кредитного периода.

ГЭ₁=100-( (40*0,21)/40*(1+0,2)¹ )+ ( (40*0,21)/40*(1+0,2)² ) + ((40*0,21+40)/40*(1+0,2)³)*100%=100-(0,175+0,145+3,328)*100%=%

ГЭ₂=100-( (40*0,18+40*0,25)/40*(1+0,2) ¹ )+ ( (40*0,19+40*0,45)/40*(1+0,2) ²+( (40*0,21+40*0,3)/40*(1+0,2) ³)*100%= 100-(0,516+0,921+0,881)*100%=-164,8%

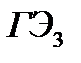=100-( (40*0,19+40)/40*(1+0,2)¹ )+ ( (40*0,19)/40*(1+0,2)² ) + ((40*0,19)/40*(1+0,2)³)*100%=-23%

Ответ: в первом банке условия предоставления лучше среднерыночных, а во втором и третьем банках условия предоставления хуже среднерыночных, поэтому условие в 1 банке принимается, а во втором и третьем не принимается.

Задача 2

Инвестор предполагает вложить 95 млн. руб. в реализацию инвестиционных проектов (проекты делимы):

Проект
Инвестиции
NPV

Сформируйте оптимальный инвестиционный портфель

Решение:

Необходимо решить индекс доходности:

;

;

;

;

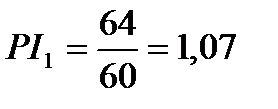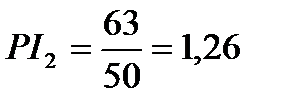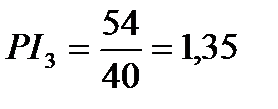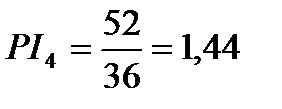Ранжируется проект в порядке убывания:

1,44 – 1,35 – 1,26 – 1,07

Проект: 4 входит полностью

3 входит полностью

2 входит не полностью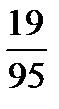

16+14+13* 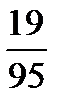=34,94 NPV портфеля.

Ответ: 34,94 NPV портфеля.

Задача 3

Для покупки оборудования кампания имеет возможность привлечь банковский кредит. Стоимость оборудования составляет 100тыс. ден. ед. Срок использования оборудования 5 лет. Номинальная ставка банковского кредита 10 %. Альтернативой вступает в лизинг: авансовый лизинговый платеж в размере 5 %; ежегодный лизинговый платеж составляет 25 тыс. ден. ед. ставка налога на прибыль 20 %.

Определить предпочтительный вариант финансирования приобретения оборудования.

Решение:

1 способ – за счет средств кредита (ставка налога на прибыль = 20%)

ДП_КР = 100*0,1*(1-0,2) / (1+0,1)¹ + 100*0,1*(1-0,2) / (1+0,1)² + 100*0,1*(1-0,2) / (1+0,1)³ +

+ 100*0,1(1-0,2) / (1+0,1)⁴ + 100/ (1+0,1)⁵ = 7,27+6,6+6,01+5,48+62,1=87,46 ден. ед.

2 способ – за счет средств лизинга:

ДП_ЛИЗИНГ = 5+(20(1-0,2)/ 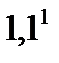+20*0,8/ 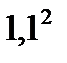+20*0,8/ 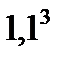+20*0,8/ 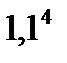+20*0,8/ 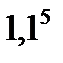) = 14,55+19,36+12,02+10,96+9,94 = 66,83 ден. ед.

Ответ: предпочтительный вариант финансирования приобретения оборудования – лизинг.

4.Оцените проекты по степени риска:

	Пессимистический сценарий	Реальный сценарий	Оптимистический сценарий
А	В	А	В	А	В
NPV, тыс. ден. ед	0,15	-0,8	2,5	4,5	4,2	8,5
Р, доля	0,8	0,05	0,6	0,7	0,3	0,25

Решение:

Математическое ожидание:

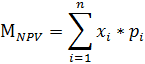
1) 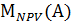= 0,15 * 0,8 + 2,5 * 0,6 + 4,2 * 0,3 = 2,88.

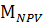(В) = -0,8 * 0,05 + 4,5 * 0,7 + 8,5 * 0,25 = 5,235.

2) дисперсия:

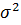(А)= (0,15-2,88)²*0,8+(2,5-2,88)²*0,6+(4,2-2,88)²*0,3 = 6,567;

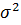(В) = (-0,8-5,235)²*0,05+(4,5-5,235)²*0,7+(8,5-5,235)²*0,25 = 4,87;

3)среднеквадратическое отклонение:

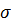(А) = ;

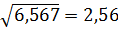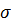(В) = ;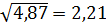

4)коэффициент вариации:

V (А) =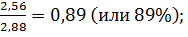

V (В) =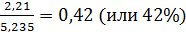

Ответ: по проекту А: 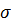= 2,56 и V = 0,89 (или 89%).

По проекту В: 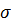= 2,21 и V = 0,42 (или 42%). Т.е., наиболее рисковый проект А, а наименее рисковый проект В.

Задача 5

Определить модифицированную норму внутренней доходности (MIRR), если цена инвестиционного капитала 8%:

Шаг расчета
Инвестиции
Доходы

Решение:

MIRR=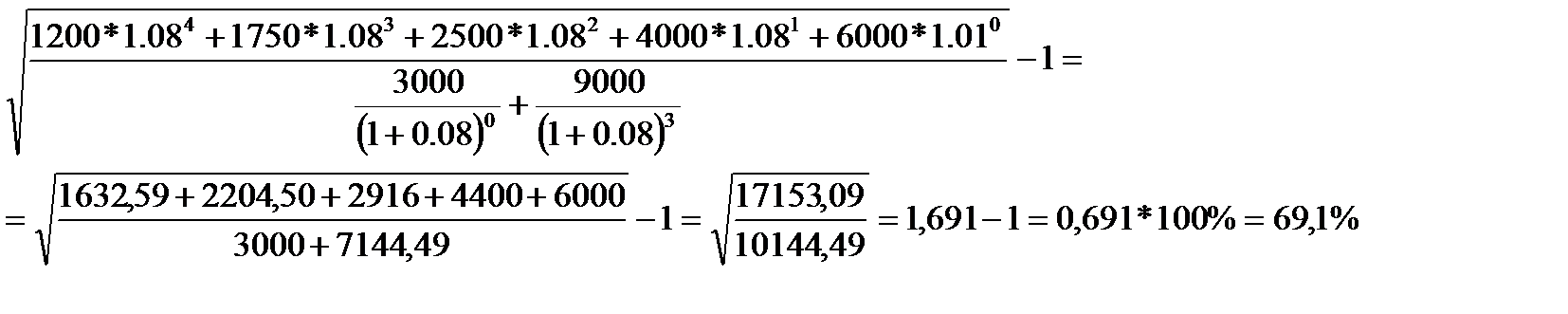

Задача 6

Предприятие рассматривает два альтернативных инвестиционных проекта, требующих инвестиций в размере 250 тыс. руб. Цена инвестируемого капитала 12%:

Денежные поступления

Проект А
Проект Б

Требуется сравнить и выбрать предпочтительный проект, используя метод цепных повторов и метод эквивалентного аннуитета.

Решение

Метод цепных повторов

1) Если рассчитать NPV для проектов

NPV=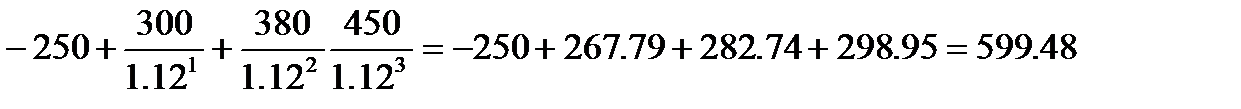

NPV=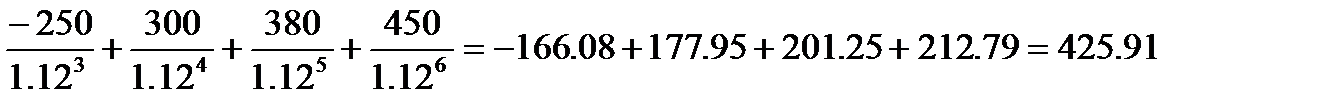

NPV =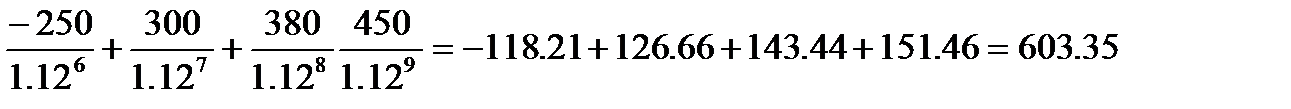

NPV =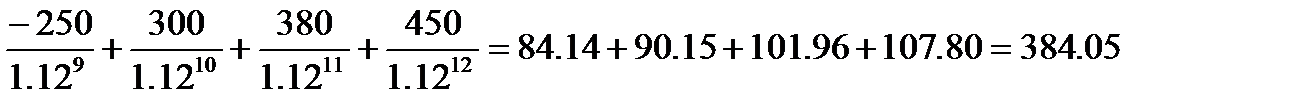

Сумма NPV=599.48+425.91+603.35+384.05=2012.79

Аналогично по проекту Б

2)Непосредственному сравнению эти данные не поддаются, поэтому необходимо рассчитать NPV повторяющихся потоков. В обоих вариантах НОК=12. В течении этого периода проект А может быть повторен 4 раза, а проект Б 3 раза.

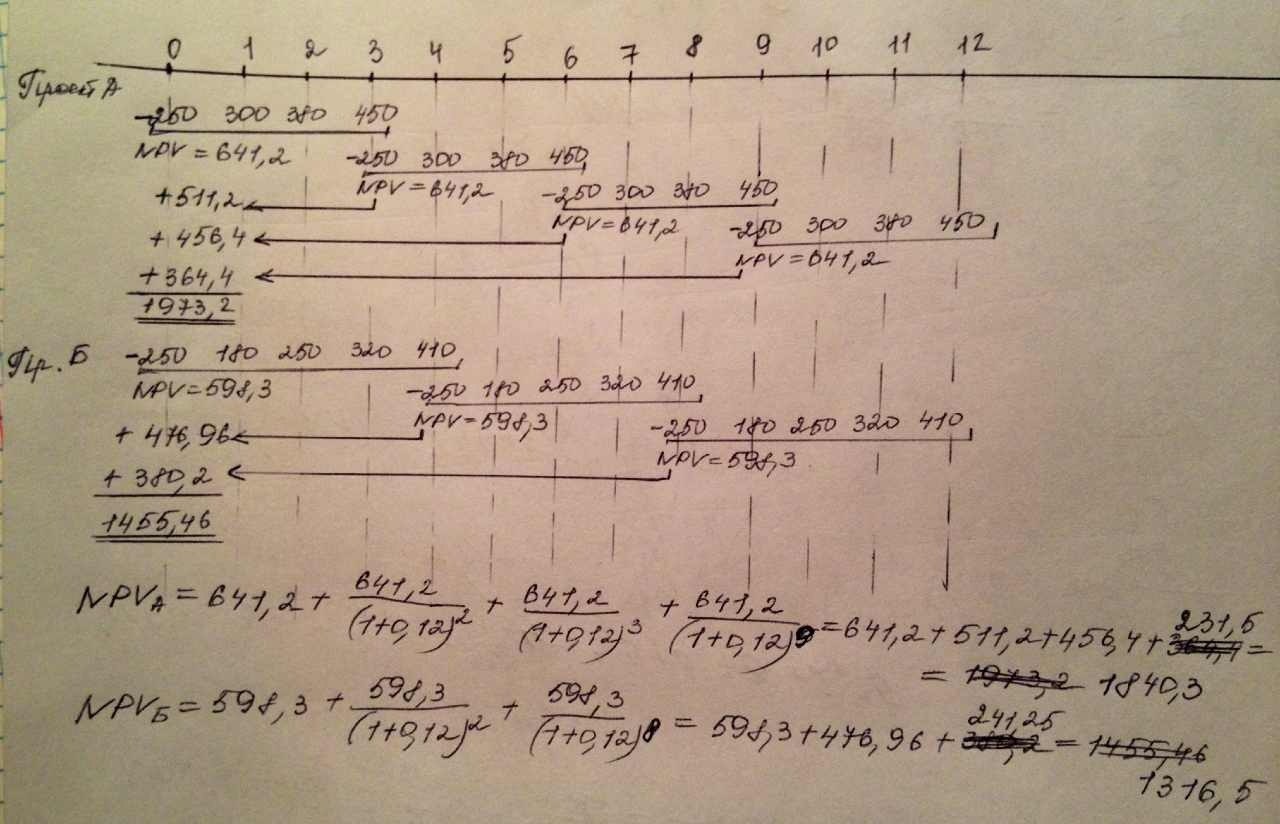
3) В случае четырехкратного повторения проекта А суммарное значение NPV равно 1840,3тыс руб, т.е.=>

NPVа=641,2 + 641,2/(1+0,12)в степ 2 + 641,2/(1+0,12) в степ 3 + 641,2/(1+0,12) в степ 9=641,2+511,2+456,4+231,5=1840,3

Где 641,2 – NPV первой реализации проекта А

511,2 – NPV второй реализации проекта А, дисконтированная к началу года 1

456,4 – NPV третей реализации проекта А, дисконтированная к началу года 1

231,5– NPV четвертой реализации проекта А, дисконтированная к началу года 1

NPVб=598,3+ 598,3/ (1+0,12)в степ 2 + 598,3/(1+0,12)в степ 8= 598,3+476,96+241,25=1316,5

Поскольку суммарный NPV в случае четырехкратной реализации проекта А больше (1840,3 тыс руб), то проект А является предпочтительным.