Уравнения связи и коэффициента корреляции

№ хозяйства n	Качество земли (балл) х	Урожайность (ц/га) у	ху	х2	у2	Теоретические (расчетные) знач. результ. пок-ля
…	…	19,5 19,0 20,5 … 33,0	…	…	380,25 361,00 420,25 … 1089,00	19,8 20,2 21,0 … 31,0
Итого		500,0			12860,00	500,0

Подставив полученные значения в систему уравнений, получим

Умножив все члены первого уравнения на 45(900/20), получим следующую систему уравнений:

Отнимем от второго уравнения первое. Отсюда

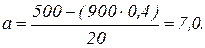
Таким образом, уравнение связи, которое описывает зависимость урожайности от качества почвы, будет иметь вид:

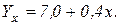
Пример

Для иллюстрации корреляционного анализа криволинейной зависимости

Если при увеличении одного показателя значения другого возрастают до определенного уровня, а потом начинают снижаться (например, зависимость производительности труда рабочих от их возраста), то для записи такой зависимости лучше всего подходит парабола второго порядка:

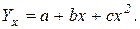
В соответствии с требованиями метода наименьших квадратов для определения параметров а, b и с необходимо решить следующую систему уравнений:

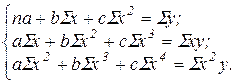
Значения 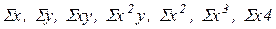находят на основании исходных данных (табл. 2).

Таблица 3.4. Зависимость производительности труда (у)

От возраста работников (х)

Средний возраст по группе (х)	Среднемесячная выработка (у)	х/10	ху	х2	х2у	х3	х4	ух
	4,2 4,8 5,3 6,0 6,2 5,8 5,3 4,4 4,0	2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0	8,4 12,0 15,9 21,0 24,8 26,1 26,5 24,2 24,0	4,00 6,25 9,00 12,25 16,00 20,25 25,00 30,25 36,00	16,8 30,0 47,7 73,5 99,2 117,4 132,5 133,1 144,0	8,00 15,62 27,00 42,87 64,00 91,13 125,00 166,40 216,00		3,93 4,90 5,55 5,95 6,05 5,90 5,43 4,78 3,70
Всего	46,0	36,0	183,0	159,00	794,0	756,00		46,00

Подставив полученные значения в систему уравнений, получим

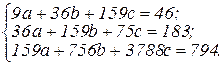
Параметры а, b и с находят способом определителей или способом исключения. Используем способ определителей.

Сначала найдем общий определитель по схеме:

Т.е.,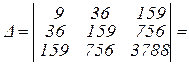

Затем находим частные определители (в них коэффициенты при соответствующих буквах заменяются на итоговые значения соответствующего уравнения в системе).

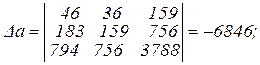
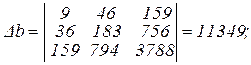
Отсюда:

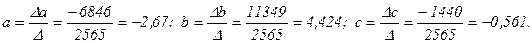
Уравнение параболы будет иметь следующий вид:

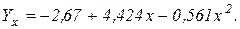
Для измерения тесноты связи между факторными и результативными показателями определяется коэффициент корреляции.

В случае прямолинейной формы связи между изучаемыми показателями коэффициент корреляции рассчитывается по следующей формуле:

.

Что касается измерения тесноты связи при криволинейной форме зависимости, то здесь используется не линейный коэффициент корреляции, а корреляционное отношение:

,

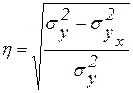где .

Тема 4. Финансовая отчетность организации и ее анализ.