Задания для самостоятельной работы. 1. Сформулируйте самостоятельно задачу расчета цены облигаций с различными входными
1. Сформулируйте самостоятельно задачу расчета цены облигаций с различными входными свойствами.
2. Обоснуйте ответ в письменном виде и сравните расчет стоимости облигаций и акций.
Используемая литература:
1. Лукасевич, И.Я. Анализ операций с ценными бумагами с Microsoft Excel/ И.Я. Лукасевич// URL: http://www.cfin.ru/finanalysis/inexcel/2-2-2.shtml (проверено 23.05.2011)
2. finekon.ru - сборник материалов по экономическим вопросам/ URL: http://www.finekon.ru/opredelenie%20stoimosti.php (проверено 23.05.2011)
3. Методика расчета НКД и доходности. URL: http://www.micex.ru/markets/stock/securities/nkd (проверено 23.05.2011)
Рекомендуемая литература:
1. Лукасевич, И.Я. Анализ операций с ценными бумагами с Microsoft Excel/ И. Я. Лукасевич. – М.: Эксмо, 2011. – 758с.
Лабораторная работа № 9
Тема: Формирование инвестиционного портфеля с помощью модели «Квази-Шарпа»
Программное обеспечение:OS Windows, MS Excel, MS Word, любой браузер, сайт www.finam.ru
Постановка целей занятия: познакомиться с формированием инвестиционного портфеля на основе модели «Квази-Шарпа».
Краткие теоретические сведения: Модели формирования инвестиционного портфеля, такие как модель Г.Марковица и У.Шарпа (Capital Asset Price Model) хорошо работают в периоды стабильного роста национальной экономики.
Это замечание относится для зарубежных фондовых рынков которые характеризуются более монотонной динамикой развития. Применение моделей Марковица и Шарпа для развивающихся рынков, в частности для фондового рынка Российской Федерации и рынка других стран СНГ, приводит к модельным ошибкам и непредсказуемым убыткам по портфелю.Это связано, с динамикой и особенностями развития данных рынков, в связи с тем, что для них свойственно: нестабильность и импульсивность доходности, сильное влияние инсайдерской (внутренней) информации, несовершенство нормативно-правовой базы, доминирующее влияние сырьевых отраслей на общую динамику развития.
Для эффективной работы на нестабильных фондовых рынках была предложена новая модель формирования инвестиционного портфеля, которая получила название модель «Квази- Шарпа». Эта модель основана на взаимосвязи доходности каждой ценной бумаги из всего множества N ценных бумаг с доходностью единичного портфеля их этих бумаг. В общих чертах модель «Квази- Шарпа» сильно походит на модель предложенную У.Шарпом, но есть некоторые отличия. Рассмотрим основные допущения модели «Квази- Шарпа»:
1. Доходность ценной бумаги рассчитывается как математическое ожидание доходностей. Это допущение есть и в модели Шарпа.
2. Единичный портфель представляет собой портфель, состоящий из всех рассматриваемых ценных бумаг, взятых в одинаковой пропорции. В модели Шарпа за эталонный портфель(бенчмарк) берется так называемый рыночный портфель, динамику которого часто описывает фондовый индекс. Для российского фондового рынка это индекс РТС (RTSI), для украинского рынка индекс ПФТС, для американского фондового рынка это S&P500.
3. Доходность ценной бумаги прямо пропорционально доходности единичного портфеля. То же предположение в модели Шарпа для рыночного портфеля.
4. Риск ценной бумаги рассчитывается как чувствительность изменения доходности ценной бумаги от изменения доходности единичного портфеля. Аналогично для модели Шарпа.
5. В отличии от модели Шарпа за безрисковую ставку берется средняя доходность единичного портфеля, а не государственные обязательства.
Модель «Квази - Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии. Формула доходности ценной бумаги следующая:
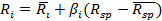, где:
Ri- доходность ценной бумаги;
Rsp- доходность единичного портфеля;
βi- коэффициент чувствительности к изменению доходности ценной бумаги, коэффициент регрессии в уравнении доходности;
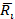–средняя доходность ценной бумаги;
– средняя доходность единичного портфеля.
Риск измеряется с помощью коэффициента бета (β), который характеризуется степенью чувствительности к изменению доходности единичного портфеля. Чем выше коэффициент бета, тем сильнее изменяется доходность ценной бумаги от колебания доходности единичного портфеля.
В модели «Квази-Шарпа » риск ценной бумаги представляет собой совокупность коэффициента бета и остаточного риска (σri). Остаточным риском называют степень разброса значений доходности ценной бумаги относительно линии регрессии.
Доходность в модели «Квази - Шарпа» рассчитывается как:
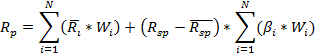
Риск же рассчитывается по следующей формуле:
Задача формирования оптимального портфеля по модели «Квази-Шарпа», где максимизируется доходность инвестиционного портфеля и устанавливается допустимый уровень риска, будет выглядеть следующим образом.
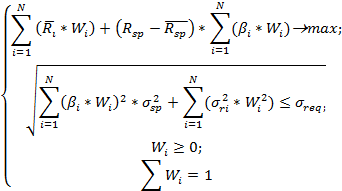
Обратная задача формирования оптимального портфеля, где минимизируется общий риск инвестиционного портфеля с фиксированным уровнем доходности, имеет следующий вид:
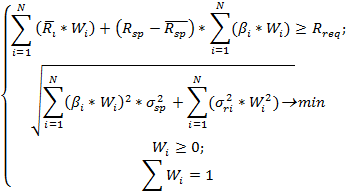
Пример.
Применить модель «Квази-Шарпа» для российского фондового рынка. Данные по котировкам взять с сайта finam.ru.Котировки взять следующих компаний: Аэрофлот (AFLT), Сбербанк (SBER), ОАО Мосэнерго (MSNG), ИнтерРАО (IUES), iO2TB (ODVA), ВТБ (VTBR).
Достижение поставленной цели осуществляется с использованием следующего алгоритма действий:
1. Мы должны зайти на сайт www.finam.ru (Рис. 1)
Рис.1 Главная страница портала finam
2. В панели инструментов выбрать инструмент «Экспорт». Появится окно. Заполним его теми значениями, которые представлены на рисунке 2.
3. Нажмем кнопку «Получить файл» и сохраним на свободное место носителя данных.
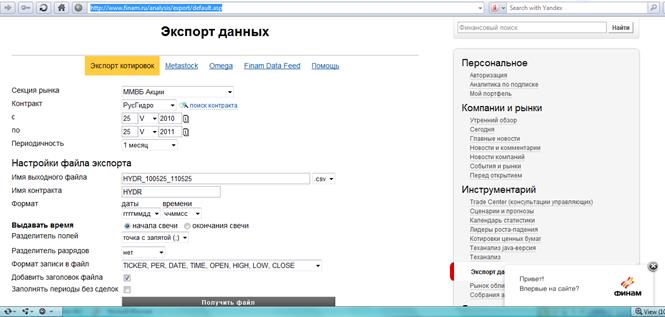
Рис. 2 Основное меню окна «Экспорт данных»
4. Аналогично заполняем данные по другим компаниям.
5. Занесем все данные в таблицу Excel. На нижеприведенном рисунке показанные месячные данные по стоимости акций этих компаний с 25.05.2010 по 25.05.2011 года.
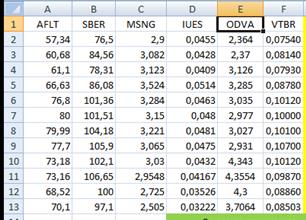
Рис. 3 Сводная таблица по котировкам акций
6. Рассчитаем доходность акций по формуле:
, где:
Ri- текущая доходность акции;
Pi- текущая стоимость акции;
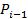– стоимость акции в предыдущем периоде.
7. Для того, чтобы рассчитать доходность акции в Excel необходимо в ячейке G3 ввести следующую формулу: (А3-А2)/А2
8. Аналогично рассчитываем доходность всех остальных акций. Для расчета необходимо выделить диапазон ячеек G3:L13. Скопировать формулу из ячейки G3 и путем специальной вставки вставить в выделенный диапазон ячеек только формулу.
Рис.4 Меню специальной вставки.
9. Для каждой акции рассчитаем среднее значение доходности за весь год, то есть за все временные отрезки по следующей формуле:
, где:
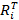- доходность i-той акции за период t;
T- рассматриваемое количество временных периодов (в данном примере это 12).
10. Для расчета средней доходности АЭРОФЛОТ необходимо в ячейке F4 прописать следующую формулу: СРЗНАЧ(G3:G13). Аналогично рассчитаем среднее значение для остальных акций. См. рис. 5.
Рис. 5 Доходность и средняя доходность акций
11. Рассчитаем доходность и среднюю доходность единичного портфеля. Доходность единично портфеля представляет собой доходность портфеля составленного из используемых акций, взятых в равных пропорциях. Доходность единичного портфеля рассчитывается следующим образом:
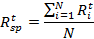
Где:
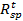–доходность единичного портфеля;
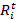- доходность i-ой ценной бумаги за период t.
Средняя доходность вычисляется по следующей формуле:
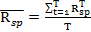, где:
Где:
– средняя доходность единичного портфеля;
Т - рассматриваемое количество временных периодов;
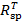– доходность единичного портфеля.
Для того, чтобы рассчитать доходность единичного портфеля (ЕП) в Excel, необходимо в ячейке M3 ввести формулу: =СРЗНАЧ(G3:L3), а для расчета средней доходности ЕП ввести в ячейку M15 формулу: =СРЗНАЧ(M3:M13). Итоговый результат представлен на рис. 6.
Рис. 6 Доходность и средняя доходность ЕП.
12. Рассчитаем чувствительность изменения доходности акции от изменения доходности единичного портфеля. Чувствительность показывает коэффициент бета (β). И формула его вычисления следующая:
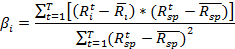
Для того, чтобы упростить расчеты необходимо подсчитать знаменатель коэффициента бета, т.к. он для всех акций будет одинаков, а после числитель.
Обозначим столбец N как знаменатель. В ячейке N3 введем формулу: =СТЕПЕНЬ((M3-$M$15);2).
В ячейке N14 происходит расчет непосредственно знаменателя по формуле: =СУММ(N3:N13).
Для вычисления числителя по периодам коэффициента бета сначала воспользуемся формулой: =(G3-$G$14)*(M3-$M$15) (Для акций Балтики, колонка О).
По аналогии заполним числители для других акций.
Суммируем полученные результаты за все периоды, то есть непосредственно рассчитываем числителя. Расчеты находятся в ячейках О14-Т14 по формулам:
= СУММ(O3:O13)
Коэффициент бета (β) будет рассчитан как отношение числителей к знаменателю:
=О14/$N$14
Рис.7 Расчет знаменателей и числителей вместе с коэффициентом β
13. Рассчитаем остаточный риск, который представляет собой степень разброса доходности ценной бумаги относительно линии регрессии. Формула расчета остаточного риска следующая:
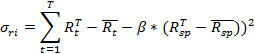
Для того, чтобы рассчитать данную формулу в табличном процессоре Excel, необходимо выполнить следующие шаги:
- Сначала рассчитываем остаточный риск на каждый период. Для этого выделим ячейку U3 и введем формулу: =СТЕПЕНЬ((F3-$F$14-$M$15*M3);2)
- После рассчитываем остаточный риск за все периоды (U14-Z14): =СРЗНАЧ(U3:U14)
14. Рассчитаем риск единичного портфеля:
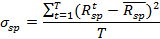
Риск единичного портфеля (Х15) будет равен: =КОРЕНЬ(N14/12)
Рис. 8 Финальный вариант таблицы
15. Сведем воедино все полученные расчетные данные в одну таблицу:
| Название | Коэффициент β | Средняя доходность | Остаточный риск |
| AFLT | 2,309 | 58 % | 3811,33 % |
| SBER | 3,764 | 93,64 % | 23426,497 % |
| MSNG | 0,031 | 1,80 % | 00,8676 % |
| IUES | 0,001 | 0,06 % | 00,0005 % |
| ODVA | -0,108 | 6,10 % | 05,7226 % |
| VTBR | 0,003 | 0,04 % | 00,001 % |
Контрольные вопросы
1. Каковы основные этапы решения задач формированию инвестиционного портфеля?
2. В чем отличие модели «Квази-Шарпа» от остальных моделей?
3. Какова формула доходности ценной бумаги?
4. Какова формула доходности ценной бумаги по модели «Квази-Шарпа»?
5. Что такое доходность единичного портфеля и зачем она рассчитывается?
6. Что такое коэффициент β?