Сокращаемые» элементы двухполюсников

– такие элементы, добавление которых в схему не изменяет числа резонансов схемы.

Выявить являются те или иные элементы сокращаемыми или нет можно двумя способами:

1). Написать аналитическое выражение Z(P) или Z(ω) приравнять числитель (найдем резонанс напряжений) и знаменатель (найдем резонанс токов), т.е. выяснить число резонансов и сравнить с числом элементов.

2). Графически построить зависимость сопротивления от частоты, выяснить число резонансов и сравнить с числом элементов.

Пример:

Возникло подозрение не являются ли элементы L₃ и C₃ сокращаемыми.

Построим график.

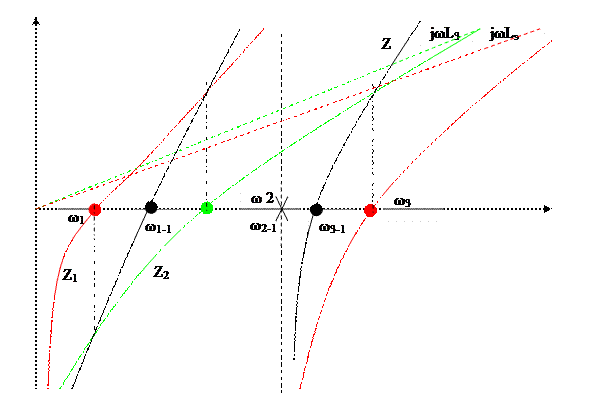
Из графика видно, что он дважды пересекает ось Z=0, т.е. имеет два резонанса напряжений и один резонанс токов. Данную схему можно представить в виде схемы имеющей 4 элемента.

Добавление L_13, C₃ не изменило общего числа резонансов, а привело к сдвигу резонансов напряжений.

ПРИМЕР: Число резонанса получилось n-3, где n – число элементов схемы, это значит, что два элемента будут сокращаемыми.

Двухполюсник с потерями.

При Z=R+jX придется рисовать два графика: фазовый и сопротивлений.

Цепи первого порядка (одноэлементный двухполюсник)

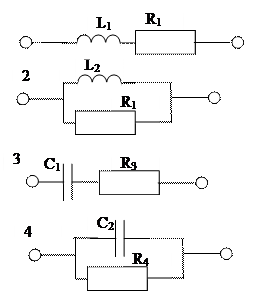
Основной характеристикой двухполюсника является частотная характеристика. Частотную характеристик можно представить в двух системах координат: комплексной и полярной системах координат.

(4.24)

; ;

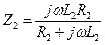Двухэлементные двухполюсники с потерями.

Здесь возможен резонанс.

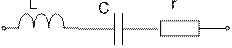
r-может быть потерями или непосредственно активное сопротивление, которое напаяны в схему.

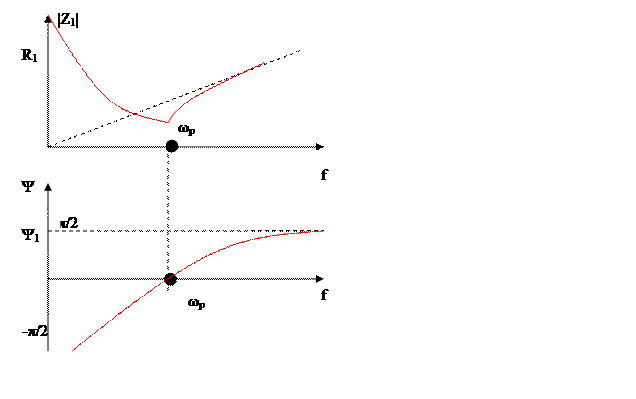
Ζ₁=r+j (ωL – )

Z=√r²+(ωL – 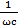) ²

Z=arctg ωL-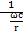

Z1

w

wрез.

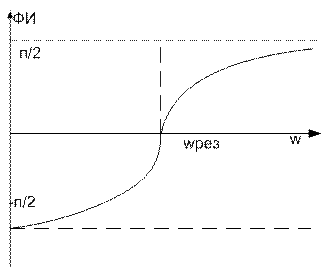
Резонанс Zm(Z1)=0

ωрез1= 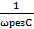ωрез =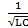

2)

Y₂= 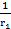+jωL+ 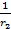+ 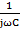= 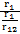+ω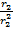²L²+ + +ω²L²+ 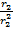+ 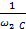=Re(Y₂)

Ym (Y₂)=- 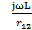+ωрез²L² + ^{= 0}

-L-ωрез²C² L r₂²₊ r₁²C+ ωрез²L² C=0

ωрез= =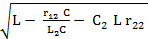

резонанс возможен в следующей ситуации

4 C> r₁² 4 C> r₁²

L/C> r₂² L/C> r₂²

L/C > r₁² L/C> r₁²

L/C< r₂² L/C< r₂²

Вывод: таким образом в параллельном контуре с потерями

1) Не всегда есть резонанс токов

2) Резонансная частота зависит не только от величин активных сопротивлений, но и от сопротивления потерь r(R)

3) Часто используют контура с очень малыми потерями

4) 4 C>> r₁² (r₂²) ωрез =

Но стабильность настройки контура (неизменность резонансной частоты) зависит не только от стабильности L и C, но и от стабильности потерь r_1, r₂.Поэтому в цепях (схемах), где нужно иметь очень стабильную частоту, контур определяющий стабильность работы устройств не должен непосредственно нагружаться, а нагрузка включается через каскад.

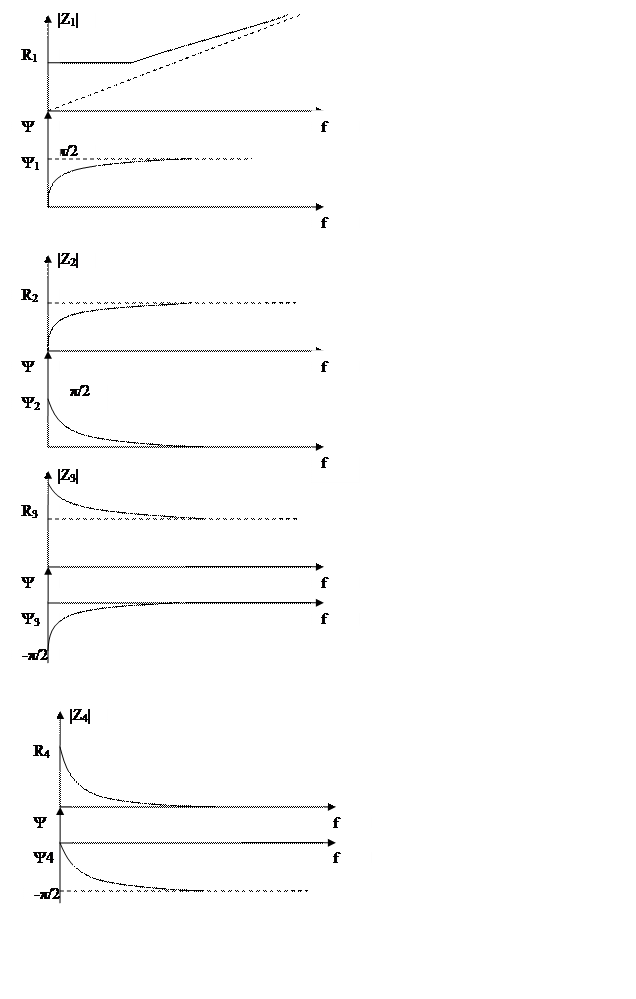
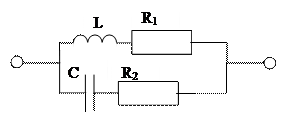
Трехэлементный двухполюсник.

Последовательный контур.

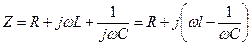
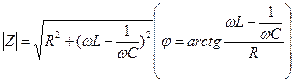
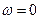
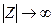
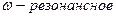
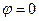
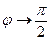
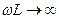
Параллельный Контур.

Im(y)

Re(y)

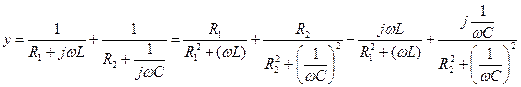
При резонансе Im(y)=0 т.е.

По формуле 4.25 делаем вывод:

1. Значение резонансной частоты зависит не только от величины реактивных элементов но и от активных сопротивлений.
2. При определении соотношениях параметров схемы резонансов нет мнимых резонансов.

Условия Резонансов:

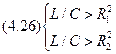
Примем в случае 4.27 резонансные свойства выявлены слабо.

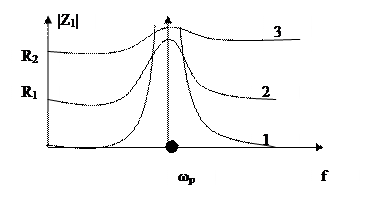
1- идеальная.

2- R₁<R₂

Для характеристики колебательной системы вводится понятие добротности.

Добротность оценивает потери в цепи и определяется отношениями энергии, запасаемой контуром (реактивным элементом) и мощности потерь .

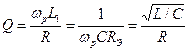
Энергия, запасаемая реактивным элементом, пропорциональна реактивному сопротивлению, а мощность потерь пропорциональна активному сопротивлению - суммарному.

Что значит суммарная мощность потерь? Т.е сюда входят омические сопротивления, входят потери из за поверхностного явления, из-за потерь диэлектрика на каркасе катушки, потери из-за излучения в окружающее пространство (на высоких частотах), вносимые потери. Вносимые потери определяются цепями, связанными с данной цепью.

При резонансе ω_резL = 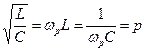(4.29)

p- характеристическое сопротивление контура.

, например Q₂>Q_{3 смотреть рисунок}

Кроме этого вводится понятие полосы пропускания (0,707).

Для колебательных контуров допускается 30 процентов снижения Rг, т.е допускается снижение по уровню П 0,1, при этом полоса пропускания увеличивается, а значит, улучшаются избирательные свойства контура. При уменьшении добротности, уменьшается полоса пропускания, и, значит уменьшаются избирательные свойства контура.

Колебательный контур с явно выраженной частотной зависимостью модуля Z можно использовать как некоторый фильтр ( избирательное устройство ), т.е может осуществляться частотная секция. Слова: избирательная, фильтрация, селекция может использовать как синонимы.

Пример: Дан контур

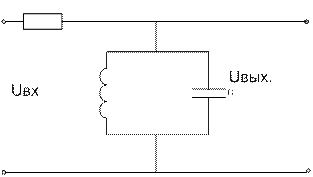
Напряжение на входе подается с неизменной амплитудой, но с изменяющейся частотой, тогда напряжение на выходе не будет постоянным, т.к зависит от частоты.

Чем дальше частота от резонансной частоты f₀ ,тем меньше Uвых., т.е контур обладает частотно-избирательными свойствами.

Полоса пропускания – это полоса частот, в которых мощность снижается не более чем в два раза.

Случай «постоянного» резонанса.

Оказывается в параллельном контуре может иметь место такое соотношение параметров, что контур будет иметь активное сопротивление на всех частотах, т.е имеет место «постоянный» резонанс.

Пусть дан контур

Каково условие, при котором имеет место «постоянный» резонанс?

Это:

r₁₌ r₂₌ r 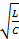₌ r²=L/C (4.30)

Докажем (4.30). Для этого запишем аналитическое выражение Ζ

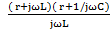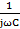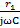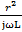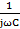Ζ= + r+ r+ = r²+rjωL+ + + 2r+ =

+ 2r+ 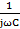= r (4.31)

Итак, сопротивление контура Ζ равно активному сопротивлению r на всех частотах при условии (4.30).

Нарисуем фазовую характеристику:

Фазовая характеристика не нужна, т.к сопротивление Ζ на всех частотах постоянно и равно r.

Найдем добротность такого контура по определению:

Q= 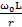≈ 1, т.к

p= ω₀L= = r

ω_{0 =}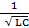

т.е мы видим, что избирательные свойства такого контура плохие, но этот контур хорош тем, что на всех частотах имеет резонанс.

Использование колебательных систем в качестве фильтрующих цепей.

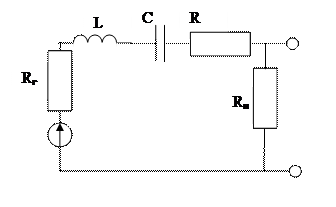
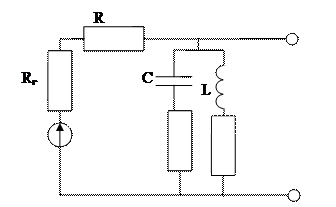
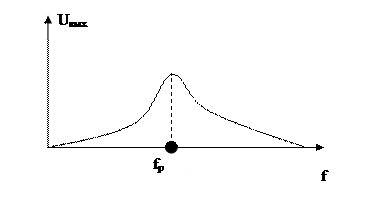
Такой контур будет давать сигналы близкие к резонансной частоте.

Степень подавления помехи:

Чем выше добротность контура, тем лучше его избирательные свойства.

Здесь получаемые противоречия между требуемой полосой пропускания и избирательностью. Увеличение Q приводит к увеличению S, а с другой стороны уменьшает полосу пропускания. Полоса пропускания может оказаться уже, чем требуется, что приведет к амплитудно-частотным искажениям. Следовательно, необходимо улучшить прямоугольности АЧХ.