Настоящая стоимость денег, ее определение и использование в финансовых расчетах

Настоящая стоимость денег—этосумма, получаемая в результате приведения будущей стоимости денег к настоящему моменту с помощью дисконтной ставки.

Если предположить простую финансовую сделку, в результате которой будущая стоимость средств (F) приводится к некоторой настоящей сумме (Р^’), то данная сделка характеризуется показателем, называемым темпом снижения (i(t)):

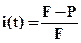. (4.36)

Темп снижения принято называть коэффициентом дисконтирования или дисконтной ставкой.

Пример 4.17. Предприятие должно вернуть в банк сумму долга в размере 500 тыс. гр. Настоящая приведенная сумма кредита, взятого на один год, составила 400 тыс. гр. Определить коэффициент дисконтирования или дисконтную ставку.

Решение:Используем формулу (4.36)

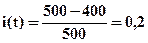или 20%.

Метод дисконтирования наиболее часто используется в операциях по учету векселей и оценки эффективности инвестиционных проектов.

Учет векселя — это решение банка купить вексель у векселедержателя.

В теории финансовых вычислений существуют два метода расчета настоящей стоимости: математический и банковский (коммерческий).

При математическом методе определения настоящей стоимости используется процентная дисконтная ставка, т.е. решается задача обратная определению наращенной суммы. Эта задача, формулируется таким образом: какую сумму денег следует дать в долг на срок (t) лет, чтобы при начислении на нее процентов по ставке (n) получить наращенную величину, равную (F).

Банковский метод определения настоящей стоимости основан на использовании учетной ставки (d), т.е. проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.

Определение настоящей стоимости денег при математическом методе предполагает использование схем простой и сложной дисконтной ставки.

Настоящая стоимость денег при использовании простой дисконтной ставки определяется по формуле:

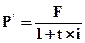, (4.37)

где P^’ — настоящая приведенная стоимость денег;

i — простая процентная дисконтная ставка;

t — срок финансовой сделки (число полных лет); в случае, когда (t) меньше 1 года, тогда 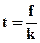(f — число дней сделки, или число дней обращения векселя, или число дней до даты погашения векселя, или число месяцев движения векселя; k — продолжительность года в днях или в месяцах; k — 365(366) дней или 12 месяцев);

F — будущая стоимость денег (будущая или номинальная стоимость векселя).

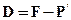. (4.38)

Пример 4.18. Банк выдал вексель сроком на 1 год, по которому можно будет получить сумму, 250 тыс. гр. Какая была внесена в банк сумма денег в момент приобретения векселя, если его доходность должна составить 11% годовых?

Решение: Используем формулу (4.37)

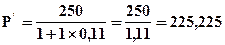тыс. гр.

Пример 4.19. Владелец векселя номинальной стоимостью 250 тыс. гр. и сроком обращения 1 год предъявил его банку — эмитенту для учета за 120 дней до даты погашения. Банк учел вексель по ставке 16% годовых. Определить сумму, полученную владельцем векселя и величину дисконта, полученную банком.

Решение: Используем формулы (4.37) и (4.38)

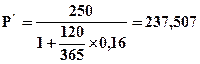тыс. гр.

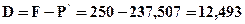тыс. гр.

Настоящая стоимость денег при использовании сложной процентной дисконтной ставки определяется по формуле:

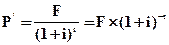, (4.39)

где 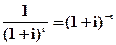— дисконтный множитель;

i — сложная процентная дисконтная ставка.

В финансовых вычислениях базовая формула (4.39), определения настоящей стоимости, может быть трансформирована с учетом различных периодов формирования денежных потоков:

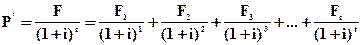, (4.40)

где F₁, F₂, F₃, … F_t — будущая стоимость денег, формирующаяся по периодам;

(1 + i)¹, (1 + i)², (1 + i)³, …, (1 + i)^t — дисконтные множители по периодам;

t — число периодов, приведения будущей стоимости к настоящему моменту времени.

Предложенная формула является базовой для оценки эффективности инвестиционных проектов. Чтобы оценить эффективность инвестиционного проекта в формулу (4.40) необходимо внести небольшие дополнения, предполагающие уменьшение настоящей приведенной стоимости на величину стартовых инвестиций. Формула для расчета может быть:

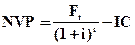, (4.41)

где NVP (net present value) — чистая приведенная стоимость;

IC — стартовые инвестиции.

Пример 4.20. Предприятие прогнозирует реализовать инвестиционный проект стоимость в 1 млн. гр. базовых инвестиций в течение одного года. Дисконтная процентная ставка установлена по проекту на уровне 12% годовых. Чистый возвратный денежный поток формируется в течение 5 лет. В первый год чистый возвратный поток составит 160 тыс. гр., во втором году — 390 тыс. гр., в третьем году 560 тыс. гр., в четвертом году — 490 тыс. гр., в пятом году — 350 тыс. гр. Оценить эффективность инвестиционного проекта, рассчитав его настоящую приведенную стоимость и сумму дисконта по данному проекту.

Решение: Используем формулу (4.41)

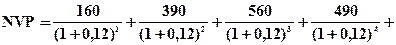
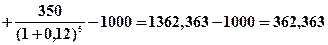
Так как полученная сумма положительная, то рассматриваемый инвестиционный проект можно признать как экономически эффективный. Однако для окончательного решения требуется подсчет и ряда других показателей, например, периода или срока окупаемости и т.п.

При начислении сложных дисконтных процентов (m) раз в году формулу (4.39) можно представить в таком виде:

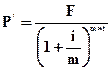, (4.42)

где 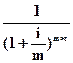— дисконтный множитель.

Для формул (4.39) и (4.42) значение дисконта может быть определено по следующим формулам:

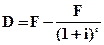. (4.43)

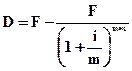. (4.44)

Пример 4.21. Определить настоящую стоимость суммы, 120 тыс. гр., которую должны выплатить через 3 года, если на первоначальную сумму начислялись сложные проценты в размере 12% годовых. Дополнительные условия: а) начисление производилось 1 раз в год; б) начисление производилось ежеквартально.

Решение: Используем формулы (4.39) и (4.42)

а) 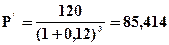тыс. гр.

б) 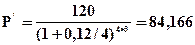тыс. гр.

При банковском методе определения настоящей приведенной стоимости денег при простой учетной дисконтной ставке расчет производится по формуле:

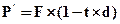, (4.45)

где d — учетная дисконтная ставка, доли единиц.

Пример 4.22. Векселедержатель предъявил для учета вексель на сумму 3 млн. гр. со сроком погашения 1 февраля текущего года. Вексель предъявлен 12.01 текущего года. Банк согласился учесть вексель с дисконтом 14% годовых. Определить сумму, которую получит векселедержатель и сумму дисконта, полученную банком.

Решение: Используем формулу (4.45)

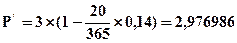млн. гр. (получил векселедержатель).

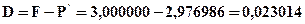или 23014 гр. (сумма дисконта).

Пример 4.23.Предприятие продало товар в кредит с оформлением простого векселя, номинальная стоимость которого 450 тыс. гр., срок векселя — 60 дней, ставка процента за кредит — 19% годовых. Через 45 дней с момента оформления векселя предприятие решило учесть вексель в банке; предложенная банком дисконтная ставка составила 15% годовых. Определить суммы, полученные предприятием и банком в результате данной сделки.

Решение:

а) определим будущую стоимость векселя к моменту его погашения:

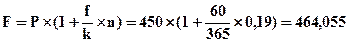тыс. гр.

б) определим срочную стоимость векселя в момент учета его банком:

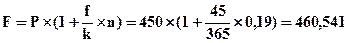тыс. гр.

в) определим сумму, которую получит предприятие:

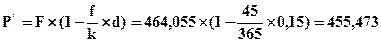тыс. гр.

г) определим сумму денег, которую получит банк за 15 дней до погашения векселя:

464,055 – 460,541 = 3,514 тыс. гр.

д) определим сумму комиссионных, полученных банком при учете векселя:

460,541 – 455,473 = 5,068 тыс. гр.

е) общая сумма средств, полученная банком при учете векселя:

3,514 + 5,068 = 8,582 тыс. гр.

Настоящая стоимость денег при сложной дисконтной учетной ставке определяется по формуле:

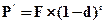. (4.46)

где d — сложная годовая дисконтная учетная ставка.

Дисконт вычисляется по формуле:

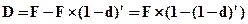. (4.47)

Сложная дисконтная учетная ставка может быть определена по формуле:

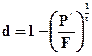. (4.48)