Линейная регрессионная модель финансовой устойчивости предприятий

Разработаем линейную регрессионную модель вида:

,

где – случайная величина, результирующий показатель, в нашем случае рентабельности активов,

– независимые переменные, в нашем случае некие финансовые коэффициенты, характеризующие предприятие,

–параметры модели, в нашем случае коэффициенты регрессии, которые необходимо найти,

– случайная ошибка модели.

Для того чтобы построить регрессионную модель необходимо найти закон, по которому будет рассчитываться результирующий показатель , характеризующий финансовую устойчивость организаций.

Значение этого показателя должно лежать для всех предприятий примерно в одних пределах. Он должен обеспечивать при этом при построении линейной регрессии минимум стандартной ошибки, значение множественного коэффициента регрессии близкого к единице, наличие не менее трех значимых коэффициентов регрессии, минимум 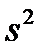, где .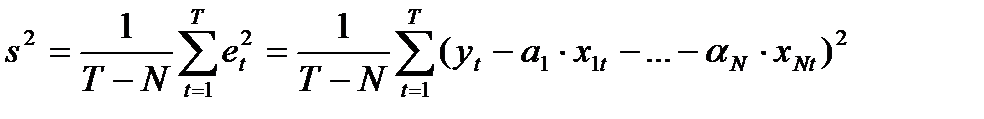

Поэтому в качестве результирующего показателя решено было выбрать показатель рентабельности активов, то есть отношение чистой прибыли к активам.

В соответствии с приложением Б формула примет вид:

.

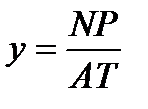Коэффициент показывает, сколько денежных единиц чистой прибыли получено на одну денежную единицу активов. Если рентабельность активов меньше процентной ставки за долгосрочные кредиты, то предприятие нельзя считать благополучным.

Разработаем сначала модель оценки финансовой устойчивости для всей группы предприятий. Для этого построим линейную регрессионные модель, в которых величина – рентабельность активов, а – это показатели отобранные ранее: 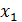– показатель доходности активов, – рентабельность собственного капитала; 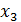– рентабельность продаж, 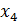– коэффициент интенсивности оборота авансируемого капитала, – показатель оборачиваемости активов, 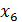– коэффициент обеспеченности собственными оборотными средствами.

Таблица 3.7 –Исходные данные

Предприятие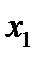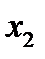
ОАО Башнефтегеофизика	0,0432	0,0967	0,6918	0,0755	18,3019	0,0011	0,0625
ОАО Лукоил	0,1072	0,2437	0,1511	0,1099	2,1703	0,0282	0,7095
ОАО Сургутнефтегаз	0,0087	0,1232	0,0092	0,2528	0,5086	0,0012	0,9451
ОАО НК Роснефть	0,0995	0,2226	0,2095	0,2367	2,2686	0,0546	0,4751
Альянс	0,0082	0,0187	0,0241	0,0230	6,5416	0,0540	0,3403
ОАО НефтеГаз-Сервис	0,0870	0,2083	0,1032	0,1484	1,2970	0,1986	0,8429
ОАО СЛАВНЕФТЬ-МЕГИОННЕФТЕГАЗ	0,0211	0,0211	0,0272	0,0401	1,3466	0,0090	0,7737
ОАО «Нефтяная компания «Мангазея»	0,1401	0,0202	0,8314	-0,3296	7,6368	0,0051	0,1685
ОАО «Ненецкая нефтяная компания»	0,7100	1,4153	0,7850	-0,8046	0,1420	0,0062	0,9044
Татнефть	0,7239	1,4478	0,8597	0,6054	0,6731	0,0443	0,8420
Нижнекаменск-нефтехим	0,1318	0,3040	0,2147	0,1382	3,2460	0,0456	0,6142
ОАО Востокгазпром	-0,0133	-0,0240	-0,0213	0,1394	0,8904	0,0007	0,6249
ОАО Томскгазпром	0,2363	0,5341	0,4245	0,3118	2,6022	0,0167	0,5566
ОАО "АК "Транснефть"	0,0056	0,0135	0,0404	0,0251	9,5581	0,3110	0,1378
СекКавНИПИгаз	0,0373	0,0978	0,0488	0,1657	1,1699	0,0795	0,7654
ТомскНИПИнефть	0,0338	0,0743	0,0895	0,0335	7,9806	0,0011	0,3781
ТНК-ВК	0,2809	0,6652	0,4216	0,0223	1,8756	0,0355	0,6663
Томская нефтегазовая компания	0,0366	0,0898	-0,6206	-0,0189	-41,305	0,0001	-0,0590
РуссНефть	0,0076	0,0158	0,0590	0,1226	10,757	0,0134	0,1289
НОВАТЭК	0,1656	0,3710	0,2975	0,3452	1,8169	0,0300	0,5565
СИБУР Холдинг	0,0324	0,6910	0,0757	0,4131	2,7508	0,0248	0,4284
НГК Славнефть	0,1073	0,2211	0,2899	0,1623	2,2350	0,0255	0,3702
СЕВМОРНЕФТЕ-ГЕОФИЗИКА	0,6688	1,5335	0,7279	0,3924	2,7126	0,0404	0,9189
ОАО "Пермнефте- геофизика"	0,3127	0,6956	0,4158	0,2144	2,9306	0,0035	0,7521
ГАЗПРОМ	0,0466	0,1137	0,0589	0,2856	0,7300	0,0265	0,7906
ЯТЭК	0,0824	0,1925	0,1240	0,3195	1,1090	0,0138	0,6639
СПМ-НЕФТЕГАЗ	0,0726	0,1761	0,1511	0,3066	2,2498	0,0045	0,4803
ОАО «АКРОН»	0,0709	0,1703	0,1363	0,2833	1,5277	0,0186	0,5202
ГАЗПРОМНЕФТЬ	0,0950	0,2162	0,2328	0,1425	4,0231	0,0055	0,4080
ООО «Газпром добыча Ямбург»	0,0026	0,0239	0,0090	0,0782	5,4763	0,0020	0,2893

Построим линейную регрессию при помощи программы Statistica 6.0. (рисунок 3.6)

Подчиненный y Умножение R ,98012629 F = 93,57693 R?= ,96064754 df = 6,23 Число случаев:30 adjusted R?= ,95038168 p = ,000000 Standard error of estimate: ,004558358 Разрыв: -,030396957 Std.Error: ,0020809 t( 23) = -1,461 p = ,1576 x1 beta=,672 x2 beta=,378 x3 beta=-,07 x4 beta=-,20 x5 beta=,045 x6 beta=,066 s^=.00799969 s=.08944098

Рисунок 3.1 –Результаты регрессии

По всем основным показателям регрессии (стандартной ошибки, множественного коэффициента регрессии, значимости коэффициентов регрессии и величине 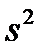) можно сделать вывод о высокой статистической точности, полученной модели. Приведем рисунок 6, график остатков этой

регрессии с доверительным интервалом. [24]

Рисунок 3.2. График остатков регрессии с доверительным интервалом

Проверим нормальность распределения остатков с помощью критерия согласия К.Пирсона («хи-квадрат»). Проверяем нулевую гипотезу: генеральная совокупность (остатки) распределена по нормальному закону. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия 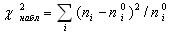и по таблице критических точек распределения 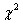, по заданному уровню значимости α и числу степеней свободы k=n–3 найти критическую точку .

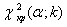Если – то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону. В нашем случае 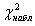=0,299, а соответствующее критическое значение при уровне значимости 0,05 составляет 42,6. Полученное значение меньше критического, а значит, принимается нулевая гипотеза.

Чтобы проверить адекватность модели, применим её к данным 2011 и 2012 годам. Как видно из рисунков 7 и 8 построенная модель хорошо описывает данные 2011 и 2012 годов.

Рисунок 3.3. Результаты применение разработанной регрессионной модели к данным 2011 года.

Рисунок 3.4. Результаты применение разработанной регрессионной модели к данным 2012 года.

Тогда модель оценки финансовой устойчивости предприятий нефтегазовой промышленности будет:

По полученной модели можно сделать вывод о том, что рост доходности положительно зависит от 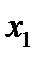(показателя доходности активов), 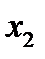(рентабельности собственного капитала), (показателя оборачиваемости активов), 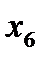( коэффициент обеспеченности собственными оборотными средствами) и отрицательно от 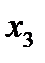(рентабельность продаж) и (коэффициент интенсивности оборота авансируемого капитала). А значит, 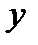положительно зависит от таких показателей бухгалтерской отчетности как работающий капитал, активы, чистая прибыль, собственный капитал, выручка от реализации и отрицательно зависит от затрат, что полностью экономически согласованно.