Простые ставки ссудных процентов

ВВЕДЕНИЕ

Особое значение для становления рыночной экономики в России имеет развитие таких процессов, как самофинансирование в его комплексном понимании, а также наращивание функционирующего капитала, прежде всего в первичном производственном звене – на предприятиях, в корпорациях и фирмах. Эти процессы опосредуются денежно-финансовыми механизмами – кредитными, налоговыми, бюджетными и т.д. Правильное управление финансами помогает любой фирме обеспечивать потребителя товарами более высокого качества и по более низким ценам, платить более высокую зарплату рабочим и менеджерам и в то же время обеспечивать более высокие доходы инвесторам, которые вложили капитал в организацию фирмы и ее последующее функционирование. Поскольку экономика как национальная, так и мировая состоит из потребителей, служащих и инвесторов, разумная финансовая политика способствует благосостоянию и отдельного человека — знание математических финансовых основ помогут правильно и выгодно взять кредит в банке, не переплатив ему лишнего рубля.

Мне, пока как потребителю, необходимо понять кредитную систему нашего государства. Моя семья много раз брала кредит на те или иные нужды. И для меня не ново такие понятия как ссудный процент или аннуитетное погашение долга. Прежде чем обратиться к кредиторам, например, я должен ознакомиться с предложениями банков, сравнить их. А банки во всем мире жонглируют цифрами так, чтобы клиент на скидку воспринимал его предложение как довольно выгодное. Да и способов жонглирования цифрами множество, даже именно этим вопросам посвящена одна из разделов специальной науки – финансовой математики. Финансовая математика – штука непростая. Разобраться в ней досконально, вспомнив даже весь школьный курс алгебры, не получится. Определившись темой моей работы, я поставил следующую цель:

- изучить основы финансовой математики, чтобы выбрать оптимальное кредитное предложение.

Для достижения этой цели нужно решить следующие частные задачи:

- ознакомление с базовыми понятиями финансовой математики;

- научиться рассчитывать способы начисления процентов, уметь определять срок кредита;

- ознакомиться с простыми ставками процентов и простыми учетными ставками, аннуитетами и ценными бумагами;

- рассмотреть сложные учетные ставки и показать различные методы начисления сложных процентов с помощью графика;

- ознакомиться с формулой И.Фишера и рассмотреть её применение на конкретных примерах;

- показать математический расчет дохода по различным видам ценных бумаг;

- составить памятку оптимального выбора кредитного предложения.

Кредит – не самоцель, а один из возможных способов решения разнообразных жизненных задач. В данный момент для нас очень важно научиться грамотно пользоваться полезной услугой под названием «кредит» – уметь сравнивать доступные варианты и выбирать более выгодное предложение, разбираться в ценообразовании и не переплачивать лишнего.

ФИНАНСОВАЯ МАТЕМАТИКА

Чтобы было четкое представление о финансовой математике, дадим определения следующих понятий:

Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т.д.), либо от инвестиций производственного или финансового характера.

Процентная ставка – это величина, характеризующая интенсивность начисления процентов.

Величина получаемого дохода (т.е. процентов) определяется исходя из величины вкладываемого капитала, срока, на который он предоставляется в долг или инвестируется, размера и вида процентной ставки (ставки доходности).

Наращивание (рост) первоначальной суммы долга – это увеличение суммы долга за счет присоединения начисленных процентов (дохода).

Множитель (коэффициент) наращивания – это величина, показывающая, во сколько раз вырос первоначальный капитал.

Период начисления – это промежуток времени, за который начисляются проценты (получается доход). В дальнейшем будем полагать, что период начисления совпадает со сроком, на которыйпредоставляются деньги. Период начисления может разбиваться на интервалы начисления.

Интервал начисления – это минимальный период, по прошествии которого происходит начислении процентов.

Существуют два способа определения и начисления процентов.

Декурсивный способ начисления процентов. Проценты начисляются в конце каждого интервала начислении. Их величина определяется исходя из величины предоставляемого капитала. Декурсивная процентная ставка ( или ссудный процент) представляет собой выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.

Антисипативный способ (предварительный) начисления процентов. Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого капитала. Определяемая таким способом процентная ставка называется (в широком смысле слова) учетной ставкой или антисипативным процентом.

В мировой практике Декурсивный способ начисления процентов получил наибольшее распространение.

При обоих способах начисления процентов процентные ставки могут быть либо простыми (если они применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления), либо сложными (если по прошествии каждого интервала начисления они применяются к сумме долга и начисленных за предыдущие интервалы процентов).

ПРОСТЫЕ СТАВКИ ССУДНЫХ ПРОЦЕНТОВ

Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон.

Введем следующие обозначения:

i (%) – простая годовая ставка ссудного процента;

i – относительная величина годовой ставки процентов;

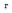I – сумма процентных денег, выплачиваемых за год;

I – общая сумма процентных денег за весь период начисления;

P – величина первоначальной денежной суммы;

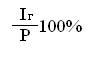
i (%) = (1.1)

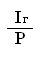
i = (1.2)

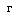I = I n (1.3)

S - наращенная сумма; S = P + I (1.4)

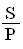
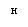k - коэффициент наращения;

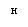k = (1.5)

n - продолжительность периода начисления в годах;

∂ - продолжительность периода начисления в днях;

K - продолжительность года в днях.

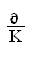
n = (1.6)

Величина K является временной базой для расчета процентов.

В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный (коммерческий) процент.

Дата выдачи и дата погашения ссуды считаются за один день. При этом возможны два варианта:

1 в. – используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответствующего дню окончания займа, вычитают номер первого дня;

2 в. – берется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням; этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.

Точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды.

Основную формулу для определения наращенной суммы можно получить, применяя последовательно формулы (1.4), (1.3), (1.2), (1.6):

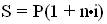(1.7)

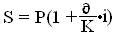или

(1.8)

На практике часто возникает обратная задача: узнать величину суммы P , которая в будущем должна составить заданную величину S. В этом случае P называется современной (текущей, настоящей, приведенной) величиной суммы S.

Определение современной величины P наращенной суммы S называется дисконтированием, а определение величины наращенной суммы S – компаундингом.

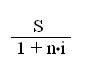Из формулы (1.7) получаем формулу, соответствующую операции дисконтирования:

P = (1.9)

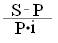Заменяя входящие в формулу (1.7) выражения на эквивалентные и выражая одни величины через другие, получаем еще несколько формул для определения неизвестных величин в различных случаях:

n = (1.10)

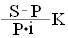
∂ = (1.11)

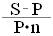
i = (1.12)

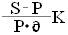
i = (1.13)

Иногда на разных интервалах начисления применяются разные процентные ставки. Если на последовательных интервалах начисленияn 1, n2, …, nn используются ставки процентов i1 , i2 , …, in , то по формулам (1.2) и (1.3) сумма процентных денег в конце первого интервала составит

I1 = P n1 i1 ,

в конце второго интервала

I2 = P n2 i2

и т.д.

При N интервалах начисления наращенная сумма составит

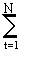
S = P (1+ nt i t) (1.14)

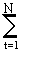Для множителя наращения, следовательно, имеем

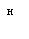k = 1+ nt i t (1.15)

Рассмотрим несколько примеров.

ПРИМЕР 1

Ссуда в размере 50 000 руб. выдана на полгода по простой ставке процентов 18% годовых. Определить наращенную сумму.

Решение:

По формуле (1.7)

S = 50 000∙(1+0,5∙0,18) = 54 500 (руб.)

ПРИМЕР 2

Кредит в размере 10 000 000 руб. выдан 2 марта до 11 декабря под 30% годовых, год високосный. Определить размер наращенной суммы для различных вариантов (обыкновенного и точного) расчета процентов.

Решение:

1. В случае точных процентов берем o = 284.

По формуле (1.8) получаем

S = 10 000 000∙(1+284/366∙0,30) = 12 327 868 (руб.)

2. Для обыкновенных процентов с точным числом дней ссуды имеем

S =10 000 000∙(1+280/360∙0,30) = 12 333 333 (руб.)

ПРИМЕР 3

Кредит в размере 20 000 000 руб. выдается на 3,5 года. Ставка процентов за первый год – 30%, а за каждое последующее полугодие она уменьшается на 1%. Определить множитель наращения и наращенную сумму.

Решение:

По формуле (1.15):

k = 1+0,3+0,5(0,29+0,28+0,27+0,26+0,25) = 1,975.

По формуле (1.14):

S =20 000 000∙1,975 = 39 500 000 (руб.)

ПРИМЕР 4

Определить период начисления, за который первоначальный капитал в размере 25 000 000 руб. вырастет до 40 000 000 руб., если используется простая ставка процентов 18% годовых.

Решение:

По формуле (1.10) получаем

n = (40 000 000-25 000 000)/(25 000 000 ∙ 0,18) = 3,33 года.

ПРИМЕР 5

Определить простую ставку процентов, при которой первоначальный капитал в размере 24 000 000 руб. достигнет 30 000 000 руб. через год.

Решение:

По формуле (1.13) определяем

i = (30 000 000-24 000 000)/ (24 000 000 ∙ 1) = 0,25 = 25%.

ПРИМЕР 6

Кредит выдается под простую ставку 26% годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 40 000 000 руб.

Решение:

По формуле (1.9) (операция дисконтирования) имеем

P = 40 000 000/ (1+250/365 ∙ 0,26) = 33 955 857 (руб.)