Аннуитет постнумерандо

Аннуитет постнумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c .

Основные количественные характеристики аннуитета постнумерандо:

1. Общая наращенная сумма определяется по формуле:

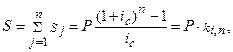
где k_i,n – коэффициент наращения в удобном для вычислений виде равен: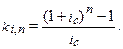

Для определения коэффициентов наращения и приведения обыкновенного аннуитета существуют таблицы, которыми удобно пользоваться в практических вычислениях. Нужно иметь в виду, что n в данном случае – не число лет, а число периодов одинаковой продолжительности (день, месяц, квартал и т. д.), в которых принята данная процентная ставка. Таким образом, если задана годовая процентная ставка, можно найти эквивалентную ей ставку на более коротком интервале и рассматривать далее п как число таких интервалов.

Таблица 3. Коэффициенты наращения аннуитета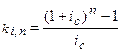

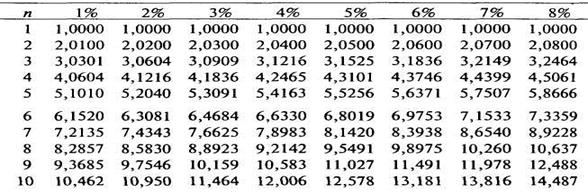
Таблица 4. Коэффициенты приведения аннуитета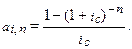

_____________________________

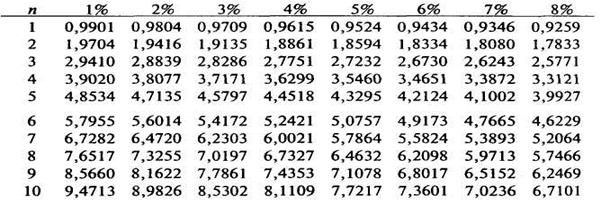2. Современная величина всего аннуитета определяется по формуле

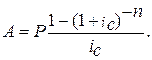
3. Современные значения каждого платежа (А_к) определяются по формуле: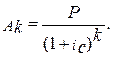

Пример 13.Для погашения пакета облигаций, выпущенных ОАО «Интерком» на 5 лет, создаётся выкупной фонд. Ежегодные платежи предприятия в него составляют 150 000 руб., на них в конце каждого года начисляются проценты по ставке 7 %. Определите итоговую наращенную сумму денежных средств, современную величину всего аннуитета и современное значение каждого платежа.

Решение. Для расчёта будущей стоимости выкупного фонда используем формулу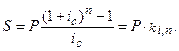

Коэффициент наращения определим по формуле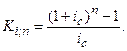

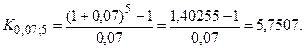
Аналогичный результат получим по таблице. Итоговая наращенная сумма будет равна S = P ∙ 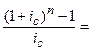150 000 ∙ 5,7507 = 862605 руб.

Современную величину всего аннуитета определим по формуле

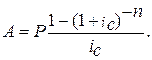
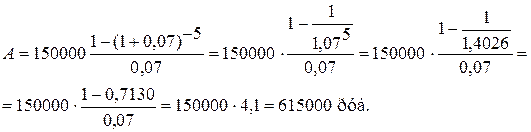
Размер очередного платежа может быть определён по формулам:

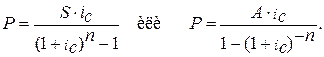
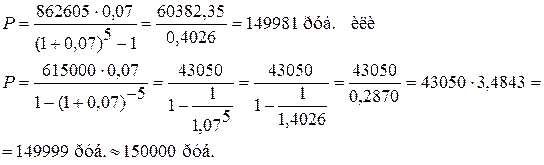
Современные значения каждого платежа (А_к) определим по формуле:

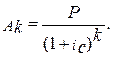
В аннуитете постнумерандо платежи и начисление процентов производится в конце года. Поэтому современная величина платежа за первый год будет равна:

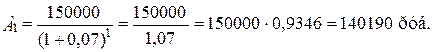
Аналогичным образом произведём дисконтирование платежей за остальные годы.

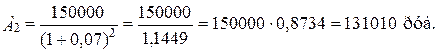
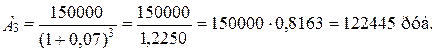
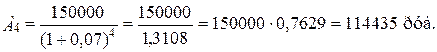
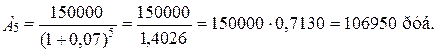
Современная величина всего аннуитета должна быть равна сумме современных значений всех платежей и начисленных процентов, т.е.

А = А₁+ А₂+ А₃+ А₄+ А₅.

В нашем примере

А = 140190+131010+122445+114435+106950=615030 615000 руб., что соответствует значению, определённому ранее по формуле.

Ответ:Полный набор показателей аннуитета составил:

- наращенная сумма денежных средств - 862605 руб.;

- современную величину всего аннуитета – 615000 руб.;

- современное значение каждого платежа: А₁ - 140190 руб.; А₂ -131010 руб.;

А₃ -122445 руб.; А₄ – 114435 руб.; А₅ - 106950 руб.

Аннуитет пренумерандо

Аннуитет пренумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c .

Очевидно, отличие от предыдущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличивается на один год, т. е. каждая наращенная сумма S_k увеличивается в (1 + i_c) раз. Следовательно, для всей суммы S_n имеем S_n =S(1 + i_c).

Для коэффициента наращения аннуитета пренумерандо получаем следующее соотношение: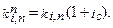

Для определения современных значений каждого платежа дисконтирование по заданной ставке i_c проводится на один раз меньше, чем в случае аннуитета постнумерандо. Поэтому каждая современная величина А_к будет больше в (1+i) раз. Таким образом, А_п = А(1 + i_c). А для коэффициента приведения a _i,n^п получаем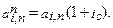

Пример 14.Найти наращенную сумму аннуитета и современную величину потока платежей, если в течение трёх лет доход, получаемый в начале года, будет составлять по 500 тыс.руб. Ставка дисконтирования – 6% годовых.

Решение.

В данном примерепоток платежей в течение трёх лет представляет собой постоянный аннуитет пренумерандо. Наращенная сумма такого аннуитета определится по формуле:

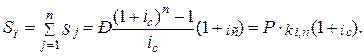
Коэффициент наращения может быть определён по таблице 3 наращенного значения аннуитета: k_{0,06; 3} = 3,1836∙(1+0,06)=3,3746.

Наращенная сумма аннуитета составит:

S^п =500∙3,3746=1687,3 тыс.руб.

Для проверки определим сумму наращенных сумм по годам.

Доход, полученный в первом году, через три года составит:

S₁=500∙(1+0,06)³=500∙1,1910=595,5 тыс.руб.; доход, полученный во втором году, S₂= 500∙(1+0,06)² = 500∙1,1236 = 561,8 тыс.руб. и доход, полученный в третьем году, S₃ = 500∙(1+0,06)¹=500∙1,06 = 530 тыс.руб.

Общая наращенная сумма S^п=S₁^п+S₂^п+S₃^п=595,5+561,8+530=1687,3 тыс.руб.

По формуле 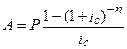(1+ 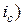можем рассчитать современную величину аннуитета. Коэффициент приведения аннуитета определим по таблице 4. Для n=3 и i_c =0,06 k_{0,06; 3} =2,6730. Тогда kⁿ =2,6730∙1,06=2,8334.

Современная величина аннуитета А^п=500∙2,8334=1416,7 тыс.руб.

Можем проверить вычисления определив сумму современных величин всех платежей и начисленных процентов. Формула современных значений каждого платежа (А_к) примет вид: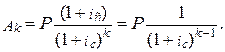

Современные величины всех платежей будут равны:

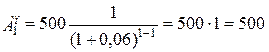тыс.руб.;

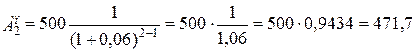тыс.руб.;

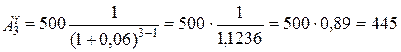тыс.руб.

Сумма современных величин всех платежей будет равна:

А^п = 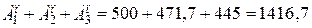тыс.руб.

Ответ:наращенная сумма аннуитета составит 1687,3 тыс.руб., а современная величина аннуитета составит 1416,7 тыс.руб.

Цель вложения денежного капитала в различного вида ценные бумаги – получение дохода и/или сохранение капитала от обесценения в условиях инфляции. Следовательно, необходимо уметь правильно оценивать реальный доход по разного вида ценным бумагам.

Вопросы для самопроверки

1. Дайте определение финансовой политики предприятия.

2. Какие стратегические цели ставят с помощью финансовой политики предприятия?

3. Что подразумевают понятия «финансовая стратегия» и «финансовая тактика»?

4. Раскройте основные направления разработки финансовой политики.

5. Кто определяет основные направления финансовой политики предприятия?

6. Перечислите основные задачи, решаемые в ходе реализации финансовой политики.

7. Перечислите основные этапы финансовой политики предприятия.

8. Что является субъектом, объектом и предметом финансовой политики предприятия?

[1] Когденко Вера Геннадьевна Краткосрочная и долгосрочная финансовая политика. –М.: ЮНИТИ-ДАНА, 2010.