Процентные ставки и методы их начисления

Финансовые вычисления, базирующиеся на понятии временной стоимости денег, - один из краеугольных элементов финансового менеджмента и используется в различных его разделах. Наиболее интенсивно они применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и др.

Логика построения основных алгоритмов основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Результативность подобной сделки может быть охарактеризована двояко: либо при помощи получаемого прироста ∆ = FV – PV, либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом – ставкой (r). Этот показатель рассчитывают отношением приращения исходной суммы к базовой величине, в качестве которой можно брать либо PV (получим процентную ставку), либо FV (получим учетную ставку).

Таким образом, в любой простейшей финансовой сделке всегда присутствуют три величины: FV, PV и ставка r, две из которых заданы, а одна является искомой. Процесс, в которой заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка (коэффициент дисконтирования), называется процессом дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором – о движении от будущего к настоящему (рис. 4.1.). Необходимо отметить, что в качестве коэффициента дисконтирования может использоваться либо процентная ставка (математическое дисконтирование), либо учетная ставка (банковское дисконтирование).

НАСТОЯЩЕЕ БУДУЩЕЕ

Исходная сумма Наращение (Возвращаемая сумма)

Процентная ставка

(Приведенная сумма) Возвращенная сумма

Дисконтирование Дисконтная ставка

Рис. 4.1. Логика финансовых операций

Экономический смысл финансовой операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку, как следует из определения процентной ставки r,

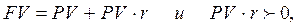(4.1.)

то видно, что время генерирует деньги или, что равнозначно, деньги имеют временную ценность.

Экономический смысл дисконтирования заключается во временном упорядочивании денежных потоков различных периодов. Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, «сегодняшнюю» стоимость будущей величины FV.

Стандартным временным интервалом в финансовых операциях является 1 год. Существуют две основные схемы дискретного начисления: схема простых и схема сложных процентов.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р, требуемая доходность – r (в долях единицы). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно растет на величину Р · r. Тогда размер инвестированного капитала через n лет (R_n) будет равен:

R_n = Р + Р · r + … + Р · r = Р · (1 + n r ) (4.2.)

Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также ранее начисленные и невостребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала к концу n-го года будет равен:

F_n = P (1 + r)ⁿ (4.3.)

Можно показать, что в случае ежегодного начисления процентов для лица, предоставляющего кредит:

- более выгодна схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

- более выгодна схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

- обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.

Схему простых процентов используют в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года. В этом случае в качестве показателя n берут величину, характеризующий удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина временных интервалов в расчетах может округляться: месяц – 30 дней; квартал – 90; полугодие – 180; год – 360 (или 365) дней. Другой весьма распространенной операцией краткосрочного характера с использованием формулы простых процентов является операция по учету векселей банком. В этом случае пользуются формулами:

(4.4.)

где d – годовая дисконтная ставка в долях единицы;

t – продолжительность финансовой операции в днях;

T – количество дней в году;

f – относительная длина периода до погашения ссуды (операция имеет смысл, если число в скобках не отрицательно).

Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этой ситуации капитал, генерирующий доходы, постоянно возрастает. Применяя простой процент, доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах либо в текущей деятельности.

Формула сложных процентов – одна из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя FM1(r,n), называемого мультиплицирующим множителем и обеспечивающего наращение стоимости, табулированы для различных значений r и n. Тогда формулу алгоритма наращения по схеме сложных процентов (формула 4.3.) можно переписать так:

F_n = P · FM1(r,n), (4.5.)

где FM1(r,n) = (1 + r)ⁿ – мультиплицирующий множитель.

Экономический смысл множителя FM1(r,n) состоит в следующем: он показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставке r (замечание: при пользовании финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки, т.е. если базисный период начисления процентов взят квартал, то в расчетах должна использоваться квартальная ставка).

В практике финансовых и коммерческих расчетов нередко оговаривается величина годового процента и частота начисления, отличная от ежегодной. В этом случае расчет ведется по формуле сложных процентов по подынтервалом и по ставке, равной пропорциональной доле исходной годовой ставки, по формуле:

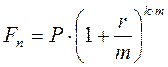(4.6.)

где r – объявленная годовая ставка;

m – количество начислений в году;

k – количество лет.

Если финансовые контракты заключаются на период, отличающийся от целого числа лет, то в этом случае проценты могут начисляться одним из двух методов:

- по схеме сложных процентов:

F_n = P · (1 + r)^{w + f} ; (4.7.)

- по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года):

F_n = P · (1 + r)^w · (1 + f · r), (4.8.)

где w – целое число лет;

f – дробная часть года.

Поскольку f < 1, то (1 + f · r) > (1 + r) ^f, наращенная сумма больше при использовании смешанной схемы.

Возможны финансовые контракты, в которых начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. В этом случае также возможно использование двух схем:

- схема сложных процентов:

(4.9.)

- смешанная схема:

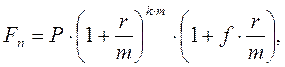(4.10.)

где k – количество лет;

m – количество начислений в году;

r – годовая ставка;

f – дробная часть подпериода.

В зависимости от частоты начисления процентов наращение суммы происходит различными темпами, причем с возрастанием частоты накопленная сумма увеличивается. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала. Из формулы (4.6.) следует:

(4.11.)

так как

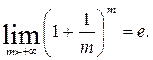(4.12.)

Таким образом, при непрерывном начислении процентов в пределах одного года используется следующая базовая формула:

F_n = P · e ^r . (4.13.)

Различными видами финансовых контрактов могут предусматриваться различные схемы начисления процентов. Как правило, в этих контрактах оговаривается номинальная процентная ставка, обычно годовая. Эта ставка, во-первых, не отражает реальной эффективности сделки и, во-вторых, не может быть использована для сопоставлений. Для того чтобы обеспечить сравнительный анализ эффективности таких контрактов, необходимо выбрать некий показатель, который был бы универсальным для любой схемы начисления. Таким показателем является эффективная годовая процентная ставка r_e, обеспечивающая переход от P к F_n при заданных значениях этих показателей и однократном начислении процентов. Она рассчитывается по формуле:

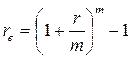(4.14.)

Из формулы (4.14.) следует, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку; две эти ставки совпадают лишь при m = 1. Именно ставка r_e служит критерием эффективности финансовой сделки и может быть использована для пространственно-временных сопоставлений.