Виды процентных ставок

Существуют различные способы начисления процентов, зависящие от условий контрактов. Соответственно применяют разные виды процентных ставок. Можно выделить ряд призна­ков, по которым различаются процентные ставки.

Для начисления процентов применяют постоянную базу начисления и последовательно изменяющуюся (за базу прини­мается сумма, полученная на предыдущем этапе наращения или дисконтирования). В первом случае используют простые, во вто­ром — сложные процентные ставки, при применении которых проценты начисляются на проценты.

Обозначим через i величину процентной ставки в десятич­ном измерении.

Можем записать следующие выражения:

TV₁ = Р + Pi = P(1 + i) — сумма, начисленная за первый год;

TV₂ = Р + Pi + Pi= P(l + 2i) - сумма, начисленная, за вто­рой год;

TV_n = P(1 + ni) - сумма, начисленная за n-й год,

Величина процента с учетом формулы определится сле­дующим образом:

I =TV_n -Р = P(1 + ni ) -Р = Pni.

Сложная процентная ставка — это такая ставка, при кото­рой процент начисляется на постоянно нарастающую базу с уче­том процентов, начисленных в предыдущие периоды («проценты на проценты»). Абсолютная сумма начисляемых процентов воз­растает, и процент увеличения суммы долга происходит с уско­рением. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капи­тализацией процентов. Имеем:

TV₁ = Р + Pi = P*(1 + i) — сумма, начисленная за первый год;

TV₂ = P*(1 + i )+P*(1+i)i=P*(1+i)² за второй год;

TV_n= P*(1 + i)ⁿ - сумма, начисленная за n-й год. (2.1.5)

Величины (1 + ni) и (1 + i)ⁿ называются коэффициента­ми (множителями) наращения простых и сложных процентов со­ответственно.

Важным является выбор принципа расчетов процентных де­нег. Существует два таких принципа:

· от настоящего к будущему,

· от будущего к настоящему.

Соответственно приме­няют ставки наращения (interest base rate) и дисконтные, или учетные, ставки (discount base rate). В финансовой литературе проценты, полученные по ставке наращения, принято называть декурсивными, по учетной ставке — антисипативными.(В России этим понятиям соответствовали проценты «на 100» и «со 100».)

Учёт векселей

В ряде случаев проценты представляют скидку с некоторой конечной суммы, принимаемой за 100%. Например, в банков­ской практике учета векселей стоимость векселя является ко­нечной суммой, с которой производится скидка по определен­ной ставке, называемой учетной.

Разница между стоимостью векселя и суммой, которую банк выдаст по этому векселю, называется дисконтом.

Обозначим учетную ставку через d. Если вексель учитывается за один год до погашения, то величина дисконта может быть определена по формуле D = TV*d, а сумма, которую получит векселедержатель (она является в данном случае первоначальной), определится так:

P =TV-TV*d= TV*(1- d).

В ситуации, когда учет происходит за несколько лет до по­гашения, формула при использовании простой учетной ставки принимает вид:

для двух лет: P = TV*(1- d)-TV*d=TV*(1-2d).

для трех лет: P = TV*(1-2d)-TV*d=TV*(1-3d);

для п лет: Р = TV* (1 – п* d).

Так же как ставка наращения, учетная ставка может быть простойи сложной. Случай простой учетной ставки рассмотрен выше.

Если используется сложная ставка, то формула расчета первоначальной суммы будет иметь вид:

P = TV*(1-d)ⁿ.

Процентные ставки могут быть фиксированными(в кон­тракте указываются их размеры) или плавающими(floating). В последнем случае указывается не сама ставка, а изменяющаяся во времени база (базовая ставка) и размер надбавки к ней — маржи.

Классическим примером базовой ставки может служить Лондонская межбанковская ставка ЛИБОР (LIBOR: London interbank offered rate). В России применяются базовые ставки по рублевым кредитам МИБОР. Размер маржи определяется рядом условий, в частности, финансовым положением заемщика, сро­ком кредита и т. д. Он может быть постоянным на протяжении срока ссудной операции или переменным.

Важное место в системе процентных ставок занимает ставка рефинансированияЦентрального Банка России — ставка, по которой ЦБ выдает кредит коммерческим банкам.

Добавим, что при последовательном погашении задолжен­ности возможны два способа начисления процентов.

Согласно первому процентная ставка (простая или сложная) применяется к фактической сумме долга.

По второму способу простые про­центы начисляются сразу на всю сумму долга без учета последо­вательного его погашения. Последний способ применяется в по­требительском кредите и в некоторых других (правда, редких) случаях.

Номинальная, периодическая и эффективная ставки.

Номи­нальная процентнаяставка — это исходная годовая ставка, кото­рую назначает банк для начисления процентов. В своей исход­ной (номинальной) величине данная ставка может быть исполь­зована при начислении процентов один раз в году. Если процен­ты начисляются более одного раза в году, то установленная ве­личина корректируется в зависимости от количества таких на­числений.

Термин «номинальная ставка» иногда используется также для обозначения процентной ставки, «не очищенной» от инфляции, в отличие от реальной — «очищенной» ставки. В этом слу­чае номинальная ставка описывает совершенно другие процес­сы, нежели начисление процентов. Равноправное хождение имеют обе трактовки номинальной ставки.

Поскольку во многих случаях проценты начисляются не­сколько раз в году, годовая ставка должна быть соответствую­щим образом преобразована. Если проценты начисляются m раз в году, то для разового начисления процентов используется так называемая периодическая ставка. Иногда ее именуют релятив­ной. Период, за который начисляются проценты, называется конверсионным.

Периодическая процентнаяставка (обозначим ее через у_р) может быть определена двумя способами.

1. Если известно количество начислений процентов в те­чение года, то:

y_m=y/m

где

у — номинальная процентная ставка;

т — количество начислений процентов в течение года.

2. Если известно количество дней, за которые начисляется процент, то:

y_p = y*z/K,

где

z — количество дней, по истечении которых осуществ­ляется разовое начисление процента;

К— принимаемое в расчет количество дней в году (К~ 360 или 365 дней).

Предположим, что начисляются сложные проценты т раз в году. По истечении первого периода, в течение которого на­числяется процент, наращенная сумма средств составит:

TV_m1= P+P*у/т=P*(1+ у/т).

По окончании второго периода:

TV_m2=P*(1 + у/т) + Р*(1 + у/т)у/т = Р*(1 + у/т)² .

В целом за год:

TV = P*(1 + y/m)^m

где

т — количество начислений процентов в течение года.

Если финансовая операция продолжается п лет, то форму­ла будет иметь вид:

TV = P*(1 + y/m)^mn

Теперь необходимо определить, во сколько раз и на сколь­ко процентов увеличивается первоначальная сумма за год. Вычтя Р из обеих частей выражения и разделив остаток на Р, находим:

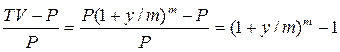
Отсюда видно, на сколько увеличилась первоначальная сумма. Переведя этот результат в процентное исчисление, име­ем:

i_э=[(1+y/m)^m -1]*100

где величина i_э — эффективная ставка.

Эта ставка измеряет тот реальный относительный доход, который получают в целом за год. Иначе говоря,

эффективная ставка — это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m.

В практических расчетах применяют так называемые дис­кретные проценты,т. е. проценты, начисляемые за фиксирован­ные интервалы времени (год, полугодие и т. д.). В некоторых слу­чаях — в доказательствах и аналитических финансовых расчетах, связанных с процессами, которые можно рассматривать как не­прерывные, в общих теоретических разработках и значительно реже на практике — возникает необходимость в применении не­прерывных процентов (continuous interest), когда наращение или дисконтирование производится непрерывно, за бесконечно малые промежутки времени. В подобных ситуациях применяют специ­альные непрерывные процентные ставки. С помощью непрерыв­ных процентов удается учесть сложные закономерности процесса наращения, например, использовать изменяющиеся по опреде­ленному закону процентные ставки.

Из курса математического анализа известно выражение:

где е — число Эйлера, которое используется как основание натурального логарифма (2,71828), или:

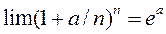
Обозначим годовую непрерывную ставку через q. Приме­нительно к случаю непрерывной ставки имеем:

Таким образом, для случая непрерывного начисления про­центов наращенная сумма за п лет определится формулой:

TV = P*e^qn

Эффективная ставка при непрерывном наращении рассчи­тывается так:

i_э=(е^q-1)*100.

Сама непрерывная ставка может быть постоянной либо изменяющейся. Причем ставка может также изменяться дис­кретно или непрерывно. Например, установлено, что за первый год непрерывная ставка составляет 2%, с начала второго года увеличивается на 1%, а с начала третьего года — еще на 1%. В этом случае коэффициент наращения за три года будет равен:

е^0,02 *e^0,03 *е^0,04 = 1,02* 1,03* 1,041 = 1,093.

Но возможна ситуация, когда сама ставка изменяется непре­рывно в течение определенного периода на заданную величину. В этом случае для расчета наращенной суммы используется формула:

где q_t — заданная функция изменения непрерывной ставки во времени.

Предположим, что ставка изменяется линейно, и функция имеет вид:

q_t =q_o+b*t,

где q_Q — величина процентной ставки на начало периода,

b — изменение ставки за год,

t - время.

Для данного вида зависимости можем записать:

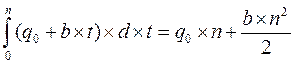
Предположим, что ставка на начало периода равна 6%, изменяется линейно и непрерывно на 1% за год. Период нара­щения — 4 года. Найти коэффициент наращения:

Дисконтирование

Временная ценность денежных вложений относится к од­ной из основных концепций, используемых в инвестиционном анализе. Необходимость учета временного фактора заставляет уделять особое внимание оценке базовых финансовых показате­лей. Разность в оценке текущих денежных средств и той же са­мой их суммы в будущем может быть связана с:

♦негативным воздействием инфляции, в связи с чем про­исходит уменьшение покупательной способности денег;

♦возможностью альтернативного вложения денежных средств и их реинвестирования в будущем (фактор упущенной выгоды);

♦ростом риска, связанного с вероятностью невозврата ин­вестированных средств (чем длительнее срок вложения капитала, тем выше степень риска);

♦потребительскими предпочтениями (лучше получить меньше доход в ближайшем периоде, чем ожидать больший, но в отдаленной перспективе).

Дисконтирование — это процесс нахождения первоначаль­ной суммы, исходя из известной величины наращенной суммы. В более общем виде математическое дисконтирование можно считать определением современной стоимости по известной ве­личине будущей стоимости.

Термин «дисконтирование» употребляется и в более широ­ком смысле — как средство определения любой стоимостной ве­личины, относящейся к будущему, на более ранний момент вре­мени. Такой прием часто называют приведением стоимостного показателя к некоторому обычно начальному моменту времени. (Приведение может быть осуществлено на любой, в том числе промежуточный момент времени.)

Величину Р, найденную с помощью дисконтирования, на­зывают современной стоимостью,или современной величиной (present value) будущего платежа TV, а иногда - текущей, или капитализированной, стоимостью. Современная величина суммы денег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения удобно учитывать такой фактор, как время. Как будет показано далее, большинст­во аналитических методов основывается на определении вре­менной величины платежей.

В зависимости от вида процентной ставки применяют два вида дисконтирования — математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором — учетная ставка.

Математическое дисконтирование представляет собой ре­шение задачи, обратной наращению первоначальной суммы ссу­ды. Задача в этом случае формулируется так: какую первона­чальную сумму ссуды надо выдать в долг, чтобы получить в кон­це срока сумму TV, при условии, что на долг начисляются про­центы по ставке I ?

Формула дисконтирования по сложным процентным став­кам наращения имеет вид:

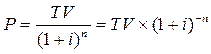
Формула дисконтирования по простым процентным став­кам следующая:

Величина i, которую мы ранее называли процентной ставкой, в процедуре дисконтирования может быть названа ставкой дисконтирования (ставкой дисконта).

Множитель (1 + i)^-n - это коэффициент (фактор) дис­контирования по сложной ставке (дисконтный множитель);

(1 + i* п)^-1 - это коэффициент (фактор) дисконтирования по про­стой ставке.

Величина каждого из коэффициентов дисконтирования меньше единицы:

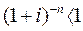и