Будущая стоимость денег, ее определение и использование в финансовых расчетах

Будущая стоимость денег (F) представляет собой сумму инвестированных в текущий момент денежных средств, в которую они перейдут через определенный период времени с учетом условий вложения [95, с. 208].

Простейшим видом финансовой сделки является однократное предоставление в долг некоторой первоначальной суммы (Р) с условием, что через некоторое время (t) будет возвращена сумма (F), которая и является будущей стоимостью денег. Данная операция характеризуется показателем темпа прироста или процентной ставкой [53, с. 157]:

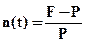(4.1)

где n(t) — темп прироста или процентная ставка;

F — будущая (возвращаемая) стоимость денег;

Р — первоначальная (исходная) сумма денег.

Из формулы (4.1) следует, что

(4.2)

Так как P ´ n(t) > 0, то можно утверждать, что время создает деньги.

Пример 4.1. Предприятие получило кредит сроком на 1 год в размере 2,5 млн. гр. с условием возврата 2,8 млн. гр. Определить процентную ставку по кредиту.

Решение: Используем формулу (4.1) и получим:

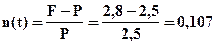или 10,7%.

Существуют две основные схемы определения будущей стоимости денег: а) схема простых процентов; б) схема сложных процентов.

Рассмотрим сущность каждой схемы.

В зависимости от того, когда производится начисление процентов, применяют два метода начисления: а) декурсивный метод — предполагает начисление процентов в конце периода, при этом используют ставки наращения; б) антисипативный метод — предполагает начисление процентов в начале периода, при этом используют учетные ставки.

Сущность схемы начисления по простым процентам или простым процентным ставкам сводится к тому, что проценты начисляются в течение всего срока финансовой сделки на одну и ту же величину денежных средств, предоставленных для вложения [66, с. 5].

Формула для определения будущей стоимости денег с использованием простых процентов может быть представлена в следующем виде:

(4.3)

где F — будущая стоимость денег по схеме простых процентов;

P — первоначальная сумма денежных средств;

n — простая процентная ставка, доли единиц;

t — срок начисления процентов (в годах).

Пример 4.2.Предприятие получило в банке кредит сроком на 3 года в размере 2 млн. гр. по ставке простых процентов, равной 12% годовых. Определить сумму накопленного долга (будущую стоимость кредита с процентами).

Решение: Из формулы 4.3 следует:

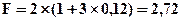млн. гр.

При использовании простых процентов очень часто период финансовой сделки не равняется целому числу лет, поэтому периоды начисления простых процентов выражаются дробным значением, т.е. как отношение числа дней или месяцев функционирования сделки к числу дней или месяцев в году:

, (4.4)

где f — число дней (месяцев) функционирования сделки;

k — продолжительность года (К=365-366 дней или 12 месяцев).

С учетом формулы (4.4) будущая стоимость денег по схеме простых процентов определяется следующим образом:

(4.5)

Пример 4.3. Банк выдал кредит предприятию 10 марта в размере 2,5 млн. гр. с условием возврата 10 июня. Простая процентная ставка установлена в размере 12,5% годовых. Определить будущую стоимость кредита по схеме простых процентов.

Решение: Продолжительность кредита составляет 93 дня с 10 марта по 10 июня включительно. Следовательно, используя формулу (4.5) получим:

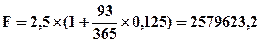гр.

При заключении финансовых соглашений процентная ставка может быть не только постоянной, но и изменяться в течение периода действия договора. В этом случае будущая стоимость денег по схеме простых процентов может быть определена по формуле:

, (4.6)

где n_i — ставка простых процентов в период i;

t_i — продолжительность (период) начисления ставки n_i;

m — число периодов начисления процентов.

При капитализации процентного дохода будущая стоимость денег по схеме простых процентов может определяться по формуле:

, (4.7)

Расчет будущей стоимости денег по простой учетной ставке определяется по формуле:

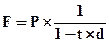, (4.8)

где F — будущая стоимость денег по простой учетной ставке;

P — сумма денег, предоставляемая в долг;

t — продолжительность финансовой сделки (годы);

d — учетная ставка, доли единиц.

Пример 4.4. Предприятие обратилось в банк за кредитом на срок 180 дней. Банк предоставляет кредит на следующих условиях: проценты (16% годовых) должны быть начислены и выплачены из суммы предоставляемого кредита в момент его выдачи. Определить общую сумму полученного кредита, если предприятию выдали сумму 600 тыс. гр.

Решение: Используем формулу (4.8)

тыс. гр.

В финансовой практике достаточно часто возникает необходимость по известным данным определить процентную (учетную) ставку или период действия финансовой сделки. Срок действия финансового соглашения может быть определен по формуле:

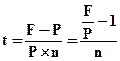. (4.9)

Если период действия финансового договора задан в днях или месяцах, то можно воспользоваться формулой:

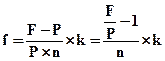, (4.10)

К = 365 (366) дней или 12 месяцев.

Пример 4.5. Предприятие желает получить кредит в сумме 500 тыс. гр. Банк предоставляет кредит по 15% годовых. На какой срок предприятие может взять кредит с тем, чтобы возвращаемая сумма не превысила 550 тыс. гр.?

Решение: Используем формулу (4.10)

дня.

Срок действия финансового соглашения при использовании учетной ставки может производиться по формуле:

, (4.11)

где t — срок ссуды в годах.

Когда срок договора определяется в днях (месяцах), то расчет ведется по формуле:

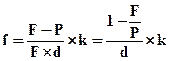, (4.12)

где f — число дней (месяцев) сделки.

Пример 4.6. Банк предоставляет кредит предприятию на условиях учетной ставки 15% годовых в размере 2 млн. гр. При выдаче кредита проценты были вычтены из установленной суммы, и предприятие получило 1,9 млн. гр. Определить на какой срок предприятие получило кредит?

Решение: Используем формулу (4.12)

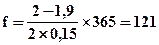день.

Если нам не известны процентная ставка или учетная ставка, то их можно определить по следующим формулам:

Процентная ставка:

. (4.13)

Учетная ставка:

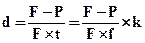. (4.14)

Пример 4.7. Предприятие обратилось в банк за кредитом в сумме 1,8 млн. гр. Банк согласился на выдачу кредита при условии, что он будет возвращен через 90 дней в размере 1850 тыс. гр. При расчете использовалась учетная ставка. Определить ее величину.

Решение:Используем формулу (4.14)

.

Схема сложных процентов в практике финансовых вычислений используется более широко, чем простых процентов. Основное отличие сложных процентов от простых состоит в том, что процесс наращения осуществляется в каждом новом периоде начисления не на первоначальную денежную сумму, а на величину с учетом капитализированных (прибавленных) процентов.

Так же как и при начислении простых процентов существует два метода начисления сложных процентов: декурсивный и антисипативный.

Будущая стоимость денег по ставке сложных процентов определяется по формуле:

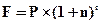, (4.15)

где F — будущая стоимость денег по ставке сложных фиксированных процентов;

P — первоначальная сумма денег;

n — годовая фиксированная ставка процента, доли единиц;

t — срок начисления (число полных лет).

Величину (1 + n) называют сложным декурсивным коэффициентом, а величину (1 + n)^{t —} множителем сложных процентов.

Пример 4.8. Инвестор вложил в банк на депозитный счет 25000 гр. под 12% годовых сроком на 3 года. Определить будущую сумму денег по схеме сложных процентов.

Решение: Воспользуемся формулой (4.15)

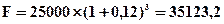гр.

В условиях рыночной экономики, когда конъюнктура финансового рынка может меняться достаточно быстро, банки используют не только фиксированные, но и плавающие сложные процентные ставки.

Будущая стоимость денег при плавающих по периодам ставкам сложных процентов определяется по формуле:

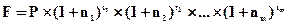, (4.16)

где n₁, n₂, …, n_m — последовательные значения ставок процентов;

t₁, t₂, …, t_m — периоды в течении которых используются соответствующие ставки процентов.

Пример 4.9. Производственное предприятие получило в банке кредит на сумму 10 млн. гр. сроком на 3 года. Процентная ставка по годам установлена в размерах: для первого года — 20% годовых, для второго года — 18% годовых, для третьего года — 15% годовых. Определить сумму долга, по истечении срока кредита.

Решение: Используем формулу (4.16)

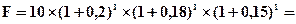
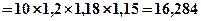млн. гр.

Пример 4.10. Предприятие получило кредит в банке на сумму 10 млн. гр. на срок 5 лет. Процентная ставка по годам плавающая: первый и второй год — 22% годовых, третий и четвертый год — 18% годовых, пятый год — 16% годовых. Определить сумму долга, подлежащую погашению по истечении срока кредита.

Решение: Используем формулу (4.16)

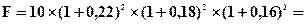
млн. гр.

Если срок финансовой сделки выражен дробным числом, то в таких случаях начисление процентов может выполняться двумя способами:

а) по формуле сложных процентов

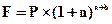, (4.17)

где t = a + b — период сделки; (а — целое число лет, b — дробная часть года).

б) смешанным способом

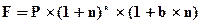. (4.18)

При t = b<1, т.е. при общем сроке менее года, будущая стоимость денег по смешанному методу будет больше, т.к. (1 + b ´ n) > (1 + n)^b.

В практике финансовых вычислений очень часто предусматривается внутригодовое начисление процентов с их капитализацией. Годовая ставка в этом случае называется номинальной, а для внутригодовых начислений указывается число периодов (m), по которым производится начисление процентов в течение года. В этом случае будущая стоимость денег при внутригодовых начислениях определяется по формуле:

, (4.19)

где m — число периодов начисления процентов в году.

Пример 4.11. Вкладчик положил на депозитный счет 10 тыс. гр. на 2 года с условием поквартального начисления процентов. Процентная ставка 12%. Проценты сложные. Определить будущую стоимость денег через 2 года.

Решение: Используем формулу (4.19)

тыс. гр.

В финансовых вычислениях по схеме сложных процентов часто возникает необходимость по известным данным определить период действия финансовой сделки или процентную ставку.

Срок действия финансовой сделки можно определить по формулам:

а) при наращении по номинальной ставке процентов:

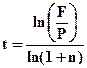. (4.20)

б) при условии внутренних начислений (m) раз в год:

. (4.21)

Номинальная процентная ставка определяется по формуле:

. (4.22)

Процентная ставка при внутригодовых начислениях определяется по формуле:

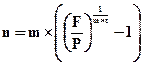. (4.23)

Различными видами финансовых соглашений могут быть предусмотрены различные схемы начисления процентов. Чтобы облегчить сравнительный анализ эффективности таких договоров необходимо иметь показатель, который был бы универсальным для любой схемы начисления. Таким показателем может быть эффективная годовая процентная ставка (r), которая обеспечивает переход от первоначальной величины вложенной суммы (Р) к будущей стоимости денежных средств (F) при заданных значениях этих показателей.

По Е.М. Четыркину [102, с. 44] множители номинальной и эффективной ставок должны быть равны:

. (4.24)

Откуда эффективная годовая процентная ставка равна:

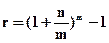. (4.25)

Из формулы (4.25) следует, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом (m) она увеличивается.

Пример 4.12. Предприятие может получить ссуду на следующих условиях:

1) ежемесячного начисления процентов по ставке 14% годовых;

2) ежеквартального начисления процентов по ставке 16% годовых;

3) полугодового начисления процентов по ставке 18% годовых;

4) годового начисления процентов по ставке 20% годовых.

Какой вариант начисления более предпочтителен для предприятия?

Решение: Воспользуемся формулой (4.25)

1) 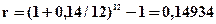или 14,9%;

2) 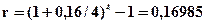или 17,0%;

3) или 18,8%;

4) или 20%.

Расчет эффективной годовой процентной ставки показывает относительные расходы предприятия по обслуживанию ссуды. Чем выше эффективная ставка, тем больше уровень расходов предприятия.

Следовательно, вариант (1) наиболее предпочтителен для предприятия, т.к. удельный вес расходов по обслуживанию ссуды составляет только 14,9% против 17%, 18,8%, 20% при других вариантах начисления.

Начисление процентов на первоначально вложенную сумму денежных средств может производиться очень часто, поэтому такой процесс начисления можно рассматривать как непрерывный. В этом случае используются непрерывные проценты. Суть непрерывных процентов заключается в том, что количество периодов наращения стремится к бесконечности, а временной интервал между периодами начисления — к нулю [66, С. 56].

Обозначим ставку непрерывных процентов (q), тогда будущая стоимость денег в пределах одного года определяется по формуле:

. (4.26)

Если процесс непрерывного начисления процентов продолжается больше 1 года, то формула будущей стоимости принимает вид:

. (4.27)

Из взаимосвязи процентной и непрерывной ставок следует:

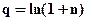, (4.28)

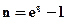. (4.29)

Начисление сложных антисипативных процентов производится аналогично расчету простых антисипативных процентов. С этой целью для определения будущей стоимости денег при использовании сложных антисипативных процентов применяется формула:

, (4.30)

где — коэффициент наращения при вычислении сложных антисипативных процентов;

d — учетная ставка сложных процентов;

t — число лет;

P — первоначальная сумма денег;

F — будущая стоимость денег.

Если наращение по сложным антисипативным процентам производится (m) раз в год, то будущая стоимость денег определяется по формуле:

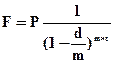, (4.31)

где m — число периодов начисления процессов в год.

Пример 4.13.Сумма 40 тыс. гр. положена в банк на 2 года. По условиям договора начисления процентов производится по сложной учетной ставке d=10% годовых. Определить будущую стоимость денег.

Решение: Используем формулу (4.30)

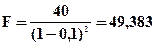тыс. гр.

Как уже отмечалось ранее, инфляционные процессы являются одним из факторов изменения стоимости денег во времени. Поэтому в финансовых расчетах необходимо учитывать инфляционный фактор.

Для определения будущей стоимости денег с учетом инфляции по схеме сложных процентов может быть использована формула:

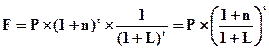, (4.32)

где F_L — будущая стоимость денег с учетом инфляции по схеме сложных процентов;

P — первоначальная сумма вложенных денег;

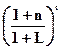— множитель наращения, учитывающий среднегодовые темпы инфляции;

t — число полных лет;

n — номинальная ставка процентов;

L — темп прироста инфляции;

(1+L)^t=J_t — индекс инфляции за t период.

Пример 4.14. Вкладчик вложил в банк сумму равную 10 тыс. гр. на срок 3 года под 12,5% годовых. Темп прироста инфляции составит 6,5% в год. Определим будущую стоимость денег с учетом инфляционного фактора. Для расчета используется сложная процентная ставка.

Решение: Используем формулу (4.32)

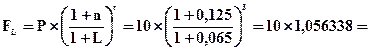
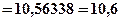тыс. гр.

Для уменьшения воздействия инфляции и компенсации потерь от снижения покупательной способности денег используются различные методы. Одним из них является индексация процентной ставки. Сущность этого метода заключается в том, что процентная ставка корректируется в соответствии с темпом инфляции. Величина корректировки оговаривается в договоре.

Процентную ставку, скорректированную на темп инфляции можно определить по формуле:

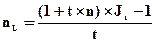, (4.33)

где J_t — индекс инфляции за t период;

t — срок финансовой сделки;

n — номинальная процентная ставка;

n_L — процентная ставка, скорректированная на индекс инфляции.

Пример 4.15. Банк выделил кредит на 8 месяцев в размере 300 тыс. грн. Ожидаемый уровень инфляции — 0,5% в месяц, требуемая реальная доходность операции равна 16% годовых. Определить ставку процентов по кредиту с учетом инфляции, будущую стоимость выданной суммы, величину процентного платежа.

Решение: Используем формулы (4.32) и (4.33)

или 22,8%.

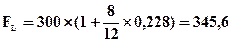тыс. гр.

Процентный платеж = 345,6 – 300 = 45,6 тыс. гр.

При выдаче долгосрочных кредитов сложная ставка процента (n_L), обеспечивающая при годовом уровне инфляции (L) реальную эффективность финансовой операции (n), определяется по формуле:

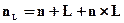. (4.34)

Пример 4.16. Предприятие получило кредит в размере 5 млн. гр. на 3 года. Доходность по кредиту должна составлять 20% годовых (сложные проценты). Прогнозируемый уровень инфляции 5% в год. Определить ставку процентов при выдаче кредита, а также будущую стоимость долга.

Решение: Используем формулы (4.34) и (4.32)

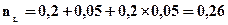или 26%.

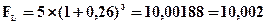млн. гр.

В том случае, когда используется величина индекса инфляции за весь срок финансовой сделки, то процентная ставка, учитывающая инфляцию, определяется по формуле:

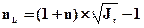. (4.35)