Начисление годовых процентов при дробном числе лет
При дробном числе лет проценты начисляются разными способами:
1) По формуле сложных процентов
S=P(1+i)n,
2) На основе смешанного метода, согласно которому за целое число лет начисляются сложные проценты, а за дробное - простые
S=P(1+i)a(1+bi),
где n=a+b, a-целое число лет, b-дробная часть года.
3) В ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т.е.
S=P(1+i)a. (2.8)
2.2.3. Номинальная и эффективная ставки процентов.
Номинальная ставка. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году m. При каждом начислении проценты капитализируются, то есть добавляются к сумме с начисленными в предыдущем периоде процентами. Каждый раз проценты начисляют по ставке j/m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле:
S=P(1+j/m)N, (2.9)
где N - число периодов начисления (N = mn, может быть и дробным числом).
Если срок ссуды измеряется дробным числом периодов начисления, то при m разовом начислении процентов в году наращенную сумму можно рассчитывать несколькими способами, приводящими к различным результатам:
1) По формуле сложных процентов
S=P(1+j/m)N/t, (3.0)
где N/t - число (возможно дробное) периодов начисления процентов, t - период начисления процентов,
2) По смешанной формуле
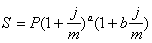 , (3.1)
, (3.1)
где a - целое число периодов начисления (т.е. a=[N/t] - целая часть от деления всего срока ссуды N на период начисления t);
b- оставшаяся дробная часть периода начисления (b=N/t-a).
Пример.Размер ссуды 20 млн. руб. Предоставлена на 28 месяцев. Номинальная ставка равна 60% годовых. Начисление процентов ежеквартальное. Вычислить наращенную сумму в трех ситуациях: 1) когда на дробную часть начисляются сложные проценты, 2) когда на дробную часть начисляются простые проценты 3) когда дробная часть игнорируется. Результаты сравнить.
Решение.
Начисление процентов ежеквартальное. Всего имеется N = 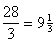 кварталов, m = 4.
кварталов, m = 4.
1) 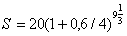 = 73,713 млн. руб.
= 73,713 млн. руб.
2) 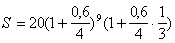 = 73,875 млн. руб.
= 73,875 млн. руб.
3) S=20(1+0,6/4)9= 70,358 млн. руб.
Из сопоставления наращенных сумм видим, что наибольшего значения она достигает во втором случае, т.е. при начислении на дробную часть простых процентов.
Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m-разовое наращение в год по ставке j/m.
Если проценты капитализируются m раз в год, каждый раз со ставкой j/m, то, по определению, можно записать следующее равенство для соответствующих множителей наращения:
(1+iэ)n=(1+j/m)mn, (3.2)
где iэ - эффективная ставка, а j - номинальная.
Отсюда получаем, что связь между эффективной и номинальной ставками выражается соотношением
Iэ=(1+j/m)m -1. (3.3)
Обратная зависимость имеет вид
j=m[(1+iэ)1/m-1]. (3.4)
Пример. Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки 10% годовых.
Решение. По формуле (3.3) находим
Iэ=(1+0,1/4)4 - 1 = 0,1038, т.е. 10,38%.
Пример. Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 12% годовых.
Решение. По формуле (3.4) находим
j = 4х[(1+0,12)(1/4)- 1]=0,11495, т.е. 11,495%.
2.2.4. Учет (дисконтирование) по сложной ставке процентов.
Здесь, также как и в случае простых процентов, будут рассмотрены два вида учета - математический и банковский.
Математический учет. В этом случае решается задача обратная наращению по сложным процентам. Запишем исходную формулу для наращения сложных процентов S = P(1+i)n и решим ее относительно P
Р = S /(1+i)n =S vn (3.5)
где vn = 1/(1 + i)n = (1 + i)-n (3.6)
учетный или дисконтный множитель.
Пример. Через 5 лет предприятию будет выплачена сумма 1000000 руб. Определить ее современную стоимость, при условии, что применяется ставка сложных процентов - 10 % годовых.
Решение. По формуле (3.5) находим
Р = 1000000х(1+0,10)-5= 620 921,32 руб.
Если проценты начисляются m раз в году, то получим:
Р = S /(1+ j/m)nm =S vnm
где
vn = 1/(1+j/m)nm= (1+j/m)-nm (3.7)
дисконтный множитель.
Так же, как и в случае начисления простых процентов, величину P, полученную дисконтированием S, называют современной или текущей стоимостью или приведенной величиной S. Суммы P и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме P, выплачиваемой в настоящий момент. Разность D=S-P называют дисконтом.
Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле
(3.8) 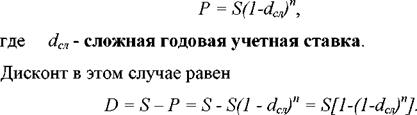 (3.9) (3.9) |
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Пример. Через 5 лет по векселю должна быть выплачена сумма 1000000 руб. Банк учел вексель по сложной учетной ставке 10 % годовых. Определить дисконт.
Решение. По формуле (3.8) находим
Р = 1000000x(1 - 0,10)5= 590490,00 руб.
D = S - P = 1000000 - 590490 = 409510 руб.
