Глава 2. Оценка риска и доходности портфеля ценных бумаг

Введение

В настоящее время важной задачей инновационного развития экономики России становится реформирование финансового сектора путем увеличения объема инвестиций, развития законодательной базы, а также повышения эффективность управления коммерческих инвестиционных банков и компаний для сбережения и увеличения вложений участников пенсионных программ, пайщиков и квалифицированных инвесторов, пользующихся услугами доверительных управляющих.

Одним из факторов, влияющих на увеличение торговых оборотов на российских биржах и как следствие на повышение инвестиционной привлекательности российских торгуемых инструментов, является грамотное портфельное инвестирование, которое позволяет диверсифицировать риски и получать ожидаемую доходность.

Для достижения наилучшего для инвестора соотношения между прибылью и риском ставится задача поиска оптимального портфеля. В зависимости от выбора критерия оптимальности существуют разные подходы к формированию оптимального портфеля. Критерий оптимальности это некоторая функция, зависящая от структуры инвестиций. Максимальное (или минимальное) значение этой функции будет соответствовать структуре оптимального портфеля.

Цель работы – расширение, углубление и систематизация знаний теоретических аспектов оптимизации портфеля ценных бумаг, а также применение их для оптимизации конкретного портфеля.

Для достижения поставленной цели были выделены следующие задачи:

· рассмотреть различные методы оптимизации портфеля ценных бумаг;

· оценить риск и доходность произвольного портфеля ценных бумаг;

· оптимизировать портфель ценных бумаг, с помощью метода Марковица.

Глава 1. Методы оптимизации портфеля ценных бумаг

Модель Марковица

В 1952 году в журнале «Journal of Finance» была опубликована статья Г.Марковица «Формирование портфеля». Статья оказала сильное влияние на теорию и практику финансовой деятельности. В дальнейшем Марковиц не переставал работать над усовершенствованием своей теории и в 1990 году получил Нобелевскую премию по экономике.

В своих работах Марковиц предложил математическую формализацию задачи по определению оптимальной структуры портфеля ценных бумаг.

В модели можно выделить ряд основных принципов:

1) рынок состоит из определенного числа активов, доходности которых для рассматриваемого периода считаются случайными величинами;

2) инвестор, основываясь на данных статистики, может рассчитать оценку ожидаемых значений доходностей, их парных ковариаций и возможности диверсификации рисков;

3) инвестор формирует любые допустимые портфели, но их доходности являются также случайными величинами;

4) при формировании портфеля рассматривается только два критерия: доходность и риск.

5) инвестор старается минимизировать риск, поэтому из двух портфелей с одинаковой доходностью предпочтительным является портфель с меньшим риском.

Основываясь на статистическом подходе, Марковиц считал, что значения доходности ценных бумаг являются случайными величинами, распределенными по нормальному (Гауссовскому) закону.

В модели Марковица доход ценной бумаги рассматривается как случайная переменная. Если по каждой ценной бумаге определить вероятности наступления дохода, то можно рассчитать распределение вероятностей получения дохода по каждой рассматриваемой альтернативе вложения средств. Данный подход известен как вероятностная модель рынка.

Эффективным Марковец считает портфель, состоящий из лучших по данной цене акций с минимальной изменчивостью доходности. Однако единственного эффективного портфеля, который был бы эффективнее всех остальных нет [12].

Доходность портфеля ценных бумаг рассматривается как средневзвешенная доходностей составляющих его ценных бумаг. И определяется по следующей формуле:

где: N — количество ценных бумаг в портфеле;

W_i— процентная доля данной бумаги в портфеле;

r_i— доходность данной бумаги.

Для измерения риска используют показатели рассеивания. Чем больше разброс величин доходов, тем больше вероятность, что ожидаемый доход не будет получен. Показателем рассеивания является среднеквадратическое отклонение.

Для определения риска портфеля ценных бумаг используется следующая формула:

где: W_a, W_b,— процентные доли данных бумаг в портфеле;

, — среднеквадратическое отклонение ценных бумаг (риск);

—коэффициент линейной корреляции.

Используя модель Марковица задачу по расчету характеристик портфеля можно представить следующим образом:

Общий риск портфеля можно состоит из двух частей: систематического (недиверсифицируемый или рыночный) риска и специфического (диверсифицируемого, собственного) риска. Рыночный риск невозможно исключить, данному риску все ценные бумаги подвергаются практически в равной степени. Специфический риск же можно избежать при помощи диверсификации. На рис. 1 представлено графическое отображение данной ситуации [4].

Рис.1 Риск портфеля и диверсификация.

При диверсификцию портфеля возникает проблема численного определения относительных долей отдельных ценных бумаг в портфеле, наиболее выгодных для владельца.

Марковиц ограничивал решение модели тем, что из всего множества «допустимых» портфелей (удовлетворяющих ограничениям), необходимо выделить те, которые рискованнее, чем другие. При помощи разработанного Марковицем метода критических линий можно выделить неперспективные портфели, в результате чего остаются только эффективные портфели. Отобранные портфели содержат сведения о процентом соотношении отдельных ценных бумаг, а также о доходе и риске портфелей. Инвестор выбирает оптимальный портфель, обеспечивающий максимальную ожидаемую доходность для некоторого уровня риска или минимальный риск для некоторого значения ожидаемой доходности». Набор портфелей, удовлетворяющих условиям, составляет эффективное множество. На рисунке 2 представлены недопустимые, допустимые и эффективные портфели, а также линия эффективного множества.

Рис. 2 Допустимое и эффективное множество портфелей

При выборе инвестором оптимального портфеля ценных бумаг также используют кривые безразличия. С помощью кривых предпочтение инвестора можно представить в графической форме.

Рис. 3 Выбор оптимального портфеля

Разные позиции инвестора по отношению к риску можно представить в виде карт кривых, которые отражают полезность вложений различные инвестиционные портфели. Таким образом, инвестору следует выбирать портфель, лежащий на кривой безразличия, которая расположена выше и левее остальных кривых. В этом случае, оптимальный портфель будет находится в точке касания одной из кривых безразличия самого эффективного множества. На рисунке 3 оптимальный портфель для некоторого инвестора обозначен точкой O.

Модель Шарпа

В Уильям Шарп первым провел регрессионный анализ рынка акций США. Шарп разработал индексную модель, упростив задачу оптимизации так, что бы расчеты оказались значительно менее трудоемкими.

Проводя анализ поведение акций на рынке, Шарп установил, что вместо определения ковариации каждой акции друг с другом достаточно установить, как каждая акция взаимодействует со всем рынком. Однако количество ценных бумаг на рынке достаточно велико и ежедневно осуществляется огромное количество сделок, поэтому цены на акции постоянно изменяются. Поэтому в качестве рыночного показателя, характеризующего движение всего рынка ценных бумаг можно использовать фондовые индексы [13].

Шарп ввел бета-коэффициент, который рассчитывается по следующей формуле:

где: – ковариация между темпами роста курса ценной бумаги и темпами роста рынка;

– дисперсия доходности рынка.

Бета-коэффициент степень зависимости отклонений доходности ценной бумаги от отклонений доходности рынка в целом. Если бета-коэффициент ценной бумаги больше единицы, то. ее цена изменяется быстрее рынка, и следовательно бумага обладает повышенной степенью риска. Соответственно если бета меньше единицы, то степень риска ценной бумаги ниже, чем в среднем по рынку

Зависимость доходности ценной бумаги от индекса рассчитывается по следующей формуле:

где: 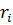– доходность ценной бумаги за период;

– доходность на рыночный индекс за период;

– коэффициент смещения;

– коэффициент наклона;

– случайная погрешность.

Если не учитывать случайную погрешность, то уравнение зависимости доходности ценной бумаги от индекса можно представить как уравнение линейной регрессии. Бета-коэффициент при этом окажется коэффициентом регрессии и, следовательно, он может быть определен по формуле:

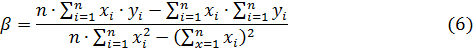
где: – доходность рынка в i-й период времени;

– доходность рынка в i-й период времени;

– количество периодов.

Коэффициент смещения (сдвига) в модели Шарпа определяет составляющую доходности ценной бумаги, которая не зависит от движения рынка и определяется по формуле:

Коэффициент альфа можно рассматривать мерой недо- или переоценки рынком ценной бумаги. Положительное значение коэффициента говорит о переоценке рынком данной бумаги, отрицательное – о недооценке рынком данной бумаги.

Разница между действительным и ожидаемым значениями при известной доходности рыночного индекса объясняется наличием случайной погрешности, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, вычисляемым по следующей формуле:

Для характеристики ценной бумаги можно использовать и другие параметры. Так коэффициент детерминации, равный квадрату коэффициента корреляции цены отдельной бумаги и рынка, при этом он изменяется в пределах от нуля до единицы и определяет степень согласованности движения рынка и бумаги. Рассчитывается коэффициент по формуле:

Если коэффициент равен единице, то бумага полностью коррелирует с рынком, если равен нулю, то движение рынка и ценной бумаги абсолютно независимы.

На развитых западных рынках значения альфа, бетта коэффициентов и коэффициента детерминации рассчитываются для всех ценных бумаг и публикуются вместе с индексами. На основе данной информации инвестор может формировать свой портфель ценных бумаг.

Достоинством модели Шарпа является математическое обоснование взаимосвязи доходности и риска [4].

Модель Тобина

Тобин провел анализ факторов, заставляющих инвесторов формировать портфель активов, а не хранить весь капитал в единственной форме. Кроме того, Тобин провел анализ адекватности количественных характеристик активов и портфелей, составляющих исходные данные в теории Марковица.

Тобин заметил, что если на рынке есть безрисковые бумаги, доходность которых не зависит от состояния рынка, то решение задачи об оптимальном портфеле значительно упрощается и приобретает новое качество.

В модели Тобина допустимыми являются любые портфели, следовательно, возможны не только покупки акций, но и их продажи. В этом случае доли акций могут быть отрицательными. Однако остается ограничение по портфелю касательно того, что сумма всех долей должна равняться 1, включая и долю безрискового актива.

Безрисковым активом считается ценная бумага, которая предлагает полностью предсказуемую ставку доходности, неопределенность стоимости такого актива отсутствует, поэтому его стандартное отклонение равно нулю, корреляция между ставкой доходности по безрисковому активу и ставкой доходности по любому другому рисковому активу равна нулю. [4]

Зависимость между ожидаемой доходностью и риском при формировании портфеля с безрисковым активом можно представить следующим образом:

где: – безрисковая ставка доходности;

– ожидаемая ставка доходности рискованного актива;

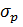– стандартное отклонение доходности рискованного актива;

Риск оптимального портфеля в зависимости от его доходности можно представить следующим образом:

где: 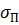– стандартное отклонение доходности портфеля;

Показатель d определяется по следующей формуле:

где: – вектор столбец долей капитала, вкладываемый в i-й вид рисковых ценных бумаг;

– матрица обратная матрице ковариаций рисковых видов ценных бумаг;

– n-мерный вектор-столбец, компоненты которого равны 1.

В матрично-векторной форме задача формирования портфеля максимальной эффективности при наличии на рынке безрисковых ценных бумаг такова:

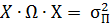
Полученный оптимальный портфель называется портфелем Тобина минимального риска, т.е. портфель Тобина это портфель Марковица при наличии на рынке безрисковых ценных бумаг[5].

Глава 2. Оценка риска и доходности портфеля ценных бумаг