Способы представления чисел

Раздел 3. Технические средства информационных технологий

Лекция № 7. Представление чисел в ЭВМ

Способы представления чисел.

Форматы представления чисел с фиксированной и плавающей

Запятой.

Литература: 1. Основы вычислительной техники и программирование:

Учебник / Под ред. Ю.А.Бузунова.- М.: Воениздат, 1981.

2.Вычислительные машины, системы и сети: Учебник /

А.П.Пятибратов, С.Н.Беляев и др.; Под ред. проф. А.П.Пя-

тибратова. – М.: Финансы и статистика, 1991.

Способы представления чисел

В ЭВМ, обычно, используются только положительные числа. Это позволяет существенно упростить схемную реализацию арифметическо-логического устройства (АЛУ). Однако при этом возникает проблема кодирования от­рицательных чисел.

В обычной практике, т. е. при ручном счете, на бумаге положительным числам приписывается знак « + », а отрица­тельным – знак « – ». В вычислительной технике для этих целей в разрядную сетку ЭВМ вво­дится специальный знаковый разряд, который занимает место перед числовыми разрядами (крайний слева). При этом для кодиро­вания знака «плюс» в знаковый разряд помещается цифра «0», а знака «минус» – цифра «1». Знаковый разряд от числовых при за­писи числа на бумаге будем отделять точкой.

Таким образом, любое двоичное число может быть представлено в следующем виде:

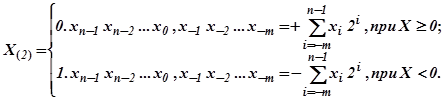
Такое представление двоичного числа называется прямым кодом этого числа и обозначается [Х] _ПК.

При условии, что | Х | < 1 (т. е. если кодируются только правильные дроби), прямой код числа можно представить следующим образом

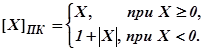
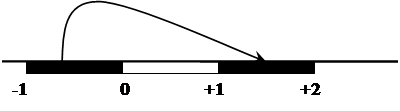
Таким образом, положительная правильная дробь может приобретать значения в диапазоне от 0 до 1, а отрицательная – в диапазоне от 1 до 2. На рисунке 1 показана числовая прямая, на которой отображены диапазоны положительных и отрицательных чисел, используемых в ЭВМ в прямого коде, для случая, когда двоичные числа представляются в виде правильных дробей.

Рисунок 1 – Перенос отрицательного числа в область

положительных чисел

Пример.

Представить числа А₍₁₀₎ = 5 и В₍₁₀₎ = -11 в прямом двоичном коде:

А₍₂₎ = 101, [А]_ПК = 0. 101;

В₍₂₎ = - 1011, [В]_ПК = 1. 1011.

В памяти вычислительной машины положительные и отрицательные числа хранятся в прямом коде. В этом же коде выполняется сложение положительных чисел, перемножение модулей чисел и некоторые другие операции. Однако использование прямого кода для вычитания и деления двух чисел требует применения специальных устройств, что существенно усложняет АЛУ. С целью упрощения реализации арифметических операций, для алгебраического представления чисел (то есть для представления чисел с учетом их знака) применяют специальные коды. За счет этого облегчается определение знака результата операции, а операция вычитания числазаменяетсянаоперацию сложения.

Такими специальными кодами являются обратный код числаи дополнительный код числа.

Примечание: Положительные числа в прямом, обратном и дополнительном кодах имеют одинаковую форму записи.

Переход от прямого кодакобратному для отрицательных чисел выполняется по правилу:

Чтобы представить отрицательное двоичное число в обратном коде, нужно оставить в знаковом разряде 1, а во всех значащих разрядах заменить 1 на 0, а 0 на 1. Такая операция называется инвертированием.

Это же правило справедливо и при переводе отрицательных чисел из обратного кода в прямой.

Пример:

Найти обратный код числа А = - 10110,1011.

А = - 10110,1011.

[A]_ПК = 1.10110,1011,

[А]_ОК = 1.01001,0100.

Пример:

Найти прямой код числа [A]_ОК = 1.1011,011.

[A]_ОК = 1.1011,011,

[А]_ПК = 1.0100,100.

Примечание: В обратном коде отрицательного числа нули, записанные в конце числа (после запятой) и в начале числа (после единицы, отде­ленной точкой), отбрасывать нельзя.

Переход от прямого кода к дополнительномудля отрицательных чисел может быть выполнен двумя способами:

Правило 1. Чтобы перевести отрицательное число из прямого кода в до­полнительный, необходимо сначала получить обратный код этого числа, а затем прибавить единицу к младшему разряду (естественно, с учетом переносов между разрядами).

Это же правило справедливо и при переводе отрицательных чисел из дополнительного кода в прямой, то есть прямой код отрицательного числа получают путем об­разования дополнительного кода от дополнительного (получают об­ратный код числа и к нему прибавляют единицу младшего разряда).

Правило 2. Чтобы перевести отрицательное число из прямого кода в до­полнительный, необходимо оставить в знаковом разряде 1, а во всех значащих разрядах (слева направо) заменить 1 на 0, а 0 на 1, за исключением последней единицы и следующих за ней нулей.

Пример:

Перевести число А = - 11,011 в дополнительный код.

[А]_ПК = 1.11,011, [А]_ОК = 1.00,100

+ 1

[А]_ДК = 1.00,101

Пример:

Перевести число А = - 100 11,101 в дополнительный код.

[А]_ПК = 1.100 11,101

[А]_ДК = 1. 01100,011

Пример: Перевести число А = 1.11011,101 из дополнительного кода в

прямой.

[А]_ДК = 1.11011,101

[А]_ПК = 1.00100,011

Модифицированный код

В разрядной сетке ЭВМ количество разрядов, отводимых для представления двоичных кодов чисел, ограничено. Поэтому при сложении двух чисел с одинаковыми знаками сумма может оказаться большей по модулю, чем максимальное число, которое можно поместить в разрядную сетку при заданном количестве разрядов. Вследствие этого результат сложения окажется неправильным. Такое явление называется переполнением разрядной сетки.

Чтобы избежать переполнения разрядной сетки, при подготовке задачи к решению на ЭВМ вводят масштабирующие коэффициенты, позволяющие уменьшить численное значение операндов по модулю. Однако, поскольку значения чисел, получаемых в процессе решения задачи, как правило, заранее неизвестны, эта мера не исключает возможности переполнения разрядной сетки.

Одним из способов, позволяющих выявлять случаи переполнения разрядной сетки, является применение модифицированного кода. Модификация заключается во введении дополнительного знакового разряда. При этом положительные числа кодируются двумя нулями, а отрицательные – двумя единицами, например: 00.101101,011; 11.111001,101.

Появление в знаковых разрядах результата комбинаций «01» и «10» является признаком переполнения разрядной сетки. При этом может быть выработан сигнал, прерывающий процесс вычислений и предупреждающий пользователя о том, что результат вычислений будет неверным.