Онятие и виды факторного анализа.

Моделирование как основа факторного анализа

Финансово-хозяйственная деятельность экономического субъекта осуществляется в условиях взаимодействия множества внешних и внутренних факторов, являющихся причинами, движущими силами процессов и явлений. Выявление, оценка и прогнозирование влияния факторов на изменение состояния и поведения исследуемого объекта или явления лежат в основе экономического анализа.

Факторы, воздействующие на результаты финансово-хозяйственной деятельности, находятся во взаимосвязи и взаимообусловленности. Расчет и оценка влияния факторов на изменение результативных показателей называется факторным анализом. Его проведение тесно связано с моделированием факторных систем.

Моделирование – один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования.

Количественная характеристика взаимосвязанных явлений осуществляется с помощью показателей (признаков). Как уже отмечалось ранее, при изучении причинно-следственных связей показатели, характеризующие причину, называются результативными (зависимыми), а признаки (показатели), характеризующие следствие – факторными (независимыми). Совокупность результативного и факторных признаков, связанных одной причинно-следственной связью, называется факторной системой.Модель факторной системы– это математическая формула, выражающая реальные связи между анализируемыми явлениями. Процесс построения аналитического выражения зависимости называется процессом математического моделированияизучаемого явления.

В факторном анализе различают два типа связей: детерминированные (функциональные) истохастические (вероятностные).

Связь называется жестко детерминированной, или функциональной, если каждому значению фактора соответствует вполне определенное неслучайное значение результативного показателя. Связь называется стохастической (вероятностной), если каждому значению фактора соответствует множество значений результативного показателя, т. е. определенное статистическое распределение.

Жестко детерминированные модели имеют ряд особенностей:

• при детерминированном подходе факторная модель полностью замыкается на ту систему факторов, которые поддаются объединению в данную модель, границей составления такой модели является длина непрерывной цепи прямых связей;
• данный подход не позволяет разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели, таким образом, мы условно абстрагируемся от действия других факторов, а все изменение результативного показателя полностью приписываем влиянию факторов, включенных в модель;
• детерминированный анализ может проводиться для единичного объекта в отсутствии совокупности наблюдений.

Проиллюстрировать первые две особенности можно на следующем простом примере. При производстве продукции используются трудовые, материальные ресурсы, основные производственные фонды, оборотные средства. Использование этих ресурсов происходит одновременно, однако невозможно построить жестко детерминированную зависимость объема продукции от факторов использования всех ресурсов. Детерминированный подход предполагает построение модели зависимости по каждому ресурсу отдельно. При этом факторы в модели могут быть детализированы, но эта детализация не приведет к объединению показателей, характеризующих использование различных видов ресурсов, в одну модель. Таким образом, могут быть построены следующие модели:

N = R × D = R × KD × D^дн;×

N = M × μ;

N = F × f = F × УВ_а × f_а;

N = E× l,

где	N	–	объем продукции;
	R	–	среднесписочная численность работающих;
	D	–	среднегодовая выработка продукции на одного работающего;
	KD	–	количество дней, отработанных работником за год;
	Dдн	–	среднедневная выработка продукции на одного работающего;
	M	–	стоимость материальных ресурсов, потребленных в производстве;
	μ	–	материалоотдача;
	F	–	среднегодовая стоимость основных производственных фондов (ОПФ);
	f	–	фондоотдача;
	УВа	–	удельный вес активной части ОПФ в общей их стоимости;
	fа	–	фондоотдача fактивной части ОПФ;
	E	–	среднегодовые остатки оборотных активов;
	l	–	оборачиваемость оборотных активов.

Построив несколько моделей, мы получим и несколько разложений изменения объема продукции на составляющие. В первом случае мы можем определить влияние на изменение объема продукции факторов использования трудовых ресурсов (численности работающих и их среднегодовой выработки или численности работающих, среднего числа дней, отработанных одним работником. и среднедневной выработки), во втором – влияние факторов использования материальных ресурсов (стоимости материалов и материалоотдачи) и т. д.

Существуют следующие виды моделей детерминированного анализа:

• аддитивные модели – модели, в которые факторы входят в виде алгебраической суммы

n

y = Σ x_i;

i = 1

• мультипликативные модели –модели, в которые факторы входят в виде произведения

n

y = П x_i;

i = 1

• кратные модели –модели, которые представляют собой отношение факторов

y =	x1	;
x2

• смешанные модели –модели, в которые факторы входят в различных комбинациях

у =	n Σ xi i=1	,	у	=	x1	,	у	=	n П xi i=1	и т. п.
xn+1		n Σ xi i=2				xn+1

В процессе моделирования преобразованию подвергается исходная факторная система (ИФС), в качестве которой выступает, как правило, любой расчетный показатель вида 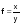, или количественный результативный показатель.

В экономическом анализе применяются следующие методы моделированияфакторных систем.

Метод удлинения – замена фактора в числителе ИФС на сумму однородных показателей. В результате может быть получена смешанная или аддитивная модель с новым набором факторов.

.

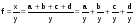Например,

,

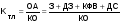где	Ктл	–	коэффициент текущей ликвидности;
	ОА	–	оборотные активы;
	КО	–	краткосрочные обязательства;
	З	–	запасы;
	ДЗ	–	дебиторская задолженность;
	КФВ	–	краткосрочные финансовые вложения;
	ДС	–	денежные средства.

Метод формального разложения – замена фактора в знаменателе ИФС на сумму однородных показателей. В результате может быть получена смешанная модель.

.

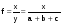Например,

ρ^А .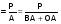

где	ρА Р	–	рентабельность активов;
	Р	–	прибыль;
	А	–	среднегодовая величина совокупных активов;
	ВА	–	среднегодовая величина внеоборотных активов;
	ОА	–	среднегодовая величина оборотных активов.

Метод расширения – умножение числителя и знаменателя дроби в ИФС на один или несколько новых показателей. В результате может быть получена мультипликативная или смешанная модель.

.

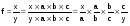Например,

ρ^СК = 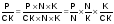= ρ^N × l^K × d,

где	ρСК	–	рентабельность собственного капитала;
	СК	–	среднегодовая стоимость собственного капитала;
	ρN	–	рентабельность продаж;
	lK	–	оборачиваемость капитала;
	d	–	структура капитала.

Метод сокращения – деление числителя и знаменателя дроби в ИФС на один и тот же новый показатель. В результате получается кратная, мультипликативная или смешанная модель с новым набором факторов.

Например,

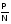ПФ	=	P	=		=	ρN	=	ρN
F + E		fемк + кзакр

где	ПФ	–	рентабельность производственных фондов;
	fемк	–	фондоемкость продукции;
	кзакр	–	коэффициент закрепления оборотных средств;
	f	–	фондоотдача основных производственных фондов;
	l	–	оборачиваемость оборотных средств.

Таким образом, изучаемый показатель может быть разложен различными приемами на составляющие (факторы) и представлен в виде модели детерминированной факторной системы.

етоды элиминирования

Основной задачей прямого факторного детерминированного анализа является оценка влияния абсолютного изменения каждого фактора на абсолютное изменение результативного показателя, т. е. разложение абсолютного изменения изучаемого показателя на столько составляющих, сколько факторов в модели.

Один из наиболее распространенных методов детерминированного факторного анализа – метод элиминирования.

Элиминированием называется логический прием последовательного абстрагирования от влияния всех факторов, кроме искомого, влияние которого определяется путем сопоставления анализируемого результативного показателя после и до изменения этого фактора.

Основным приемом элиминирования является метод цепных подстановок, который заключается в последовательной замене базисных значений каждого фактора на фактические данные отчетного периода, таким образом получается ряд промежуточных значений результативного показателя, разность двух промежуточных значений в цепи подстановок равна изменению результативного показателя за счет изменения соответствующего фактора.

Пусть y = f(a,b,c,d) – некоторая функция, характеризующая связь результативного показателя y с факторами a, b, c, d. За анализируемый период результативный показатель получил приращение Δy = y₁ – y₀, требуется определить, какой частью приращение результативного показателя обязано приращению каждого фактора, т. е. расписать следующую зависимость

Δy = Δy_a + Δy_b + Δy_c + Δy_d.

В соответствии с методом цепных подстановок

y₀ = f(a₀,b₀,c₀,d₀)

y_a = f(a₁,b₀,c₀,d₀) Δy_a = y_a – y₀

y_b = f(a₁,b₁,c₀,d₀) Δy_b = y_b – y_a

y_c = f(a₁,b₁,c₁,d₀) Δy_c = y_c – y_b

y₁ = f(a₁,b₁,c₁,d₁) Δy_d = y₁ – y_c

Δy = Δy_a + Δy_b + Δy_c + Δy_d

Метод цепных подстановок применим для моделей любого вида и имеет несколько модификаций.

Для всех видов моделей применяется прием прямого счета. Расчет влияния факторов осуществляется по следующим формулам

Δy_a = f(a₁,b₀,c₀,d₀) – f(a₀,b₀,c₀,d₀)

Δy_b = f(a₁,b₁,c₀,d₀) – f(a₁,b₀,c₀,d₀)

Δy_c = f(a₁,b₁,c₁,d₀) – f(a₁,b₁,c₀,d₀)

Δy_d = f(a₁,b₁,c₁,d₁) – f(a₁,b₁,c₁,d₀).

Совокупное влияние факторов Δy_a + Δy_b + Δy_c + Δy_d должно быть равно изменению результативного показателя Δy.

Для многофакторных моделей чаще всего применяется прием прямого счета с использованием аналитических таблиц. Для реализации этого приема строится специальная аналитическая таблица (4.1).

Таблица 4.1

Расчет влияния факторов на изменение

результативного показателя методом прямого счета

Подстановки	Взаимодействующие факторы	Результативный показатель	Влияние фактора
a	b	c	d
1. Базовые значения факторов	a0	b0	c0	d0	y0 = f(a0,b0,c0,d0)	×
2. Изменение фактора а	a1	b0	c0	d0	ya = f(a1,b0,c0,d0)	Δya = ya – y0
3. Изменение фактора b	a1	b1	c0	d0	yb = f(a1,b1,c0,d0)	Δyb = yb – ya
4. Изменение фактора c	a1	b1	c1	d0	yc = f(a1,b1,c1,d0)	Δyc = yc – yb
5. Изменение фактора d	a1	b1	c1	d1	y1 = f(a1,b1,c1,d1)	Δyd = y1 – yc
Совокупное влияние факторов	×	×	×	×	×	Δya + Δyb + + Δyc + Δyd

Другой модификацией метода цепных подстановок для мультипликативных моделейявляется метод (прием) абсолютных разностей. Так, для трехфакторной мультипликативной моделиy = a × b × c расчет влияния факторов производится следующим образом:

Δy_a = Δa × b₀ × c₀

Δy_b = a₁ × Δb × c₀

Δy_c = a₁ × b₁ × Δc.

Для мультипликативных моделейтакже можно применять прием прямого счета с использованием индексов (индексный метод). Расчет влияния факторов для трехфакторной мультипликативной модели y = a × b × c с помощью этого приема выполняется по формулам:

Δy_a = y₀ × (I_a – 1)

Δy_b = y₀ × I_a × (I_b – 1)

Δy_c = y₀ × I_a × I_b × (I_c – 1),

где	Ia	–	индекс изменения фактора a (Ia = a1 : a0);
	Ib	–	индекс изменения фактора b;
	Iс	–	индекс изменения фактора с;
	y0	–	базисное значение результативного показателя.

Расчет влияния факторов индексным методом можно произвести, используя специальную аналитическую таблицу (4.2).

Таблица 4.2

Расчет влияния факторов на изменение

результативного показателя индексным методом

Подстановки	Базовое значение результативного показателя	Индексы изменения факторов	Влияние фактора
Ia	Ib	Ic
1. Изменение фактора а	y0	Ia – 1	×	×	Δya = y0 × (Ia – 1)
2. Изменение фактора b	y0	Ia	Ib – 1	×	Δyb = y0 × Ia × (Ib – 1)
3. Изменение фактора c	y0	Ia	Ib	Ic – 1	Δyc = y0 × Ia × Ib × (Ic – 1)
Совокупное влияние факторов	×	×	×	×	Δya + Δyb + Δyc

Для мультипликативных моделей также можно использовать метод относительных разностей. Прежде всего необходимо преобразовать модель, заменив качественные показатели формулами их расчета. Например, трехфакторную мультипликативную модель y = a × b × c можно преобразовать следующим образом

y = a × b × c = a ×	d	×	y	.
a	d

Расчет влияния факторов производится по формулам:

Δy_a = y₀ × (k_a – 1)

Δy_b = y₀ × (k_d – k_а)

Δy_c = y₀ × (k_y – k_d),

где	ka	–	коэффициент изменения фактора a (ka = a1 : a0);
	kd	–	коэффициент изменения фактора d;
	ky	–	коэффициент изменения результативного показателя.

Таким образом, порядок вычислений не зависит от количества факторов в модели, а выбор конкретного приема определяется видом модели (приемы абсолютных и относительных разностей и индексный метод могут применяться только для мультипликативных моделей, а прием прямого счета – для любых).

Недостаток метода заключается в том, что результаты расчетов зависят от порядка замены факторов. В двухфакторных моделях, как правило, сначала вычисляют влияние количественного фактора при базисном значении качественного, а затем влияние качественного фактора при фактическом значении количественного, в результате чего активная роль в изменении результативного показателя часто необоснованно приписывается влиянию изменения качественного фактора.

Для того, чтобы понять причину зависимости результатов расчета от порядка замены факторов, проиллюстрируем задачу детерминированного факторного анализа для двухфакторной мультипликативной модели f = x ×y графически (рис. 4.1).

	х0 × Δy
у1
		Δх × Δy
у0
х0 × y0		Δх × y0
						х0	х1