Процесс моделирования ситуации

Такое моделирование основано на сценарном подходе.

Определение: Сценарий - совокупность тенденций, характеризующих ситуацию в настоящий момент, желаемых целей развития, комплекса мероприятий, воздействующих на развитие ситуации, и системы наблюдаемых параметров (факторов), иллюстрирующих поведение процессов.

Сценарий может моделироваться по трем основным направлениям:

1. Прогноз развития ситуации без всякого воздействия на процессы в ситуации (ситуация развивается сама по себе);
2. Прогноз развития ситуации с выбранным комплексом мероприятий (управлений) (прямая задача);
3. Синтез комплекса мероприятий для достижения необходимого изменения состояния ситуации (обратная задача).

Этапы моделирования ситуации:

• определение начальных условий, тенденций, характеризующих развитие ситуации на данном этапе. Это необходимо для придания адекватности модельного сценария реальной ситуации, что усиливает доверие к результатам моделирования. Например, начало финансовой нестабильности США в частном секторе (1991 - 2000 гг.) - см. Рис.1.- явился структурный сдвиг от профицита в размере 4.9% ВВП к дефициту в размере 4.5% ВВП.
• задание целевых, желаемых направлений (увеличение, уменьшение) и силы (слабо, сильно) изменения тенденций процессов в ситуации;
• выбор комплекса мероприятий (совокупности управляющих факторов), опре­деление их возможной и желаемой силы и направленности воздействия на ситуацию;
• выбор комплекса возможных воздействий (мероприятий, факторов) на ситуацию, силу и направленность которых необходимо определить;
• выбор наблюдаемых факторов (индикаторов), характеризующих развитие сит­уации, осуществляется в зависимости от целей анализа и желания пользователя.

Каждое из трех направлений моделирования включает в себя определенную совокупность взаимосвязанных этапов моделирования (см. табл.1).

	Направления моделирования
Этапы моделирования	1.Развитие ситуации без управляющих воздействий на процессы в ситуации (ситуация развивается сама по себе)	2. Прогноз развития ситуации с выбранным комплексом мероприятий (управлений) (прямая задача)	3. Синтез комплекса мероприятий для достижения необходимого направления развития ситуации (обратная задача)
Определение начальных условий развития ситуации	+	+	+
Задание целевых факторов направлений и силы их изменения	+	+	+
Выбор совокупности управляющих факторов и силы их воздействия		+
Выбор комплекса мероприятий, силу и направленность которых необходимо определить			+
Выбор наблюдаемых факторов (индикаторов)	+	+	+

Особенности управления сложными ситуациями

При анализе текущего состояния сложной ситуации перед пользователем неизбежно встают следующие вопросы:

1. какие модели управления следует выбрать для обеспечения желаемого поведения целевых факторов?
2. какие изменения ситуации возможны в (ближайшем) будущем?
3. какие проблемы при этом могут возникнуть?

Вопросы группы 1 - это вопросы текущего (оперативного) управления ситуацией для достижения поставленных целей. Решением этой задачи могут быть несколько вариантов "пригодного" управления. Поскольку изначально постулируется, что каждому понятию, используемому в когнитивной модели, однозначно соответствует конкретное предметное понятие, то реализация каждого найденного варианта управления предусматривает проведение соответствующих конкретных мероприятий. И тут сразу же возникает задача сравнительного оценивания этих вариантов по

• близости результатов управления к намеченной цели (по эффективности вариантов);
• по затратам (финансовым, физическим, моральным и т.п.), связанным с реализацией каждого варианта;
• по характеру последствий (обратимые, необратимые) от реализации соответствующих вариантов в реальной ситуации и т.д.

Приведем конкретные примеры работы с простейшими когнитивными мо­делями в виде когнитивных карт для случая 1 (ситуация развивается сама по себе).

+

+

Норма прибыли - v3 ( p = I / K)

-

+

-

Инфляция v2

Чистый приток иностранного капитала - v5

+

Курс доллара - v6

-

-

Инвестиции v7 ( I )

+

Финансовая стабильность - v8

+

Рис.1. Виртуальный цикл М.Вулфа анализа финансово-экономической нестабильности США.

Virtuous cycle М.Вулфа [10] представлен системой из трех положительных контуров I, II, III, часть из которых описана выше. (См. Лекцию 8)

Дуги между вершинами обозначают наличие непосредственного влияния фактора, из которого исходит стрелка (дуга), на фактор, в кото­рый входит стрелка. Например, рост притока иностранного капитала непосредственно вызывает рост курса доллара в данном месте,но не наоборот. Рост притока иностранного капи­тала вызывается не прямо ростом инвестиций (I), а увеличением финансовой стабиль­ностии ростоминдекса фондового рынка. Знак плюс у дуги означает: если фактор, из которого исходит стрелка, растет по величине, то увеличивается и характеристика, в которую входит стрелка, а если уменьшается, то уменьшается и характеристика, в которую входит стрелка. Знак минус на дуге означает противо­положную картину изменения знаков приращения в вершинах, связанных дугой.

В дополнение к этому оговаривают условия "передачи"подугам изменений харак­теристик, связанных дугами. Например: а) измене­ния любого значения фактора в вершине происходят только дискретно, через определенные промежутки времени - шаги моде­ли (через день, месяц, год и т.д.); б) изме­нения одной характери­стики передаются только по дугам за один шаг модели и в вершины, связанные дугами; в) изменения факторов в вершине с исходя­щими из нее дугами передаются с коэффициентом усиления, равным +1, если знак дуги "+", и — 1, если знак дуги равен "—",или, есливместо знаков за­даны веса, означающие коэффициент уси­ления, то равным этому весу; г) величина изменения характеристики в вершине, в которую входит несколько дуг, в случае одновременного поступления нескольких воздействий равна аддитивной сумме этиx воздействий. Совокупность этих условий называют правилом развития импульсного процесса и модели.

идент	вес фак	вес фак нач	коэф прич след связ
			v1	v2	v3	v4	v5	v6	v7	v8
v1	0.73	0.70		-0.20
v2	-0.14	0.20			-0.50				-0.33
v3	0.16	0.10	0.30			0.7
v4	0.27	0.20					0.30
v5	0.61	0.15						0.60
v6	0.49	0.40		-0.50
v7	0.63	0.70								0.50
v8	1.15	0.80					0.50

В данной таблице показана система конечно- разностных уравнений, в которой

записана "когнитивная модель", изображенная на Рис.1 Во 2-ой колонке представлено решение, в 3-ей - исходные значения факторов. Ясно, что все это справедливо, как минимум, в предположении законности "оцифрения", т.е. "хороших шкал".

Метод стабилизирующих стратегий. Метод основан на использо­вании когнитивной модели функционирования данной системы. Здесь когнитивная модель - это представление системы с помощью ориентиро­ванного графа (орграфа), дугам которого поставлены в соответствие либо знаки, либо веса отношений, отображаемых дугами. Вершинами орграфа являются основные факторы (характеристики), определяющие развитие основных событий в системе и окружающей среде. Дуги — те или иные от­ношения между ними.

В качестве другого примера рассмотрим данный на рис.2. орграф - модель дляанализа проблемы потребления электроэнергии ([11]),ставшая уже классикой.

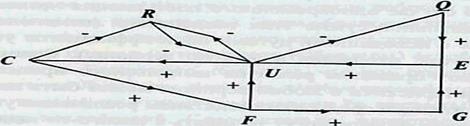
Рис.2. Знаковый орграф для анализапроблемыпотребления электроэнергии

Здесь вершины: С - энергетические мощности, F - число предпри­ятий, С—число рабочих мест; Е- населенность; Q- состояние окружаю­щей среды; И- пот­ребление энергии; R - стоимость электроэнергии. Продолжим применение логики ±.

Например, если растет потребление энергии (U}, то состояние окружающей среды {Q) ухудшает­ся, и наоборот. Изменение характеристики в любой вершине может быть навязано возму­щением из окружающей среды или следствием реали­зации управленческо­го решения. Анализ модели могут начинать с какого-то задан­ного состоя­ния системы - значений характеристик в каждой вершине в некоторый на­чальный момент времени и начального возмущения нескольких характе­ристик,

С помощью такого рода моделейможно решать ряд управленческих задач;

а) прогнозирования процессов в системе вследствие иливозмущений из окружающей среды и/или реализации управленческих решений;

6} оценки устойчивостипо Лагранжу процессов функционирования системы;

в) выработки стратегий решений, стабилизирующих по Лагранжу[2] функционирование системы;

г) ранжирования факторовпо степени потенциальной угрозы деста­билизации системы;

д) ранжирования факторов по очередности воздействий для стабили­зации системы. Такого рода возможности когнитивных моделей обсужда­ются в разделе с использованием соответствующего математического ап­парата.

Особенности применения когнитивных моделей для проблемных ситуаций 3, 4 и 5-й категории сложности.

Пример с моделью на рис.2и его обсуждение в [II] показывают,* что модель может не требовать даже точных понятий вводимых в нее факторов и характеристик. Так автор модели Робертс не уточняет понятий "энергетические мощности" (Q, "состояние окружающей среды"' (Q), "населенность", получая при этом убедительные выводы.В этом главная ценность когнитивных моделей: можно получатьинте­ресныевыводы при анализе проблемы,не прибегая к точнымколичественнымоцен­кам и отношениям. Например, бесспорно утвер­ждение, заложенное в модель, что рост числа предприятий (F) влечет за собой через неко­торое время или сразу рост числа рабочих мест в соответ­ствующем месте (городе, районе и т.д.). Этим обоснован знак дуги от F к G. И надо ли всегда знать точную коли­чественную характеристику этого воздейст­вия? Предложенный подход (в том числе Робертсом) освобождает от этого. Более того, показано, что при определенных усло­виях устойчивость по Лагранжу системы, отображаемой когни­тивной мо­делью, зависит только от структуры модели (и системы) и не зависит от возмущающих воздействий.

В итоге, единственным спосо­бом стабилизации анализируемых процессов в этиx случаях является измене­ние структуры системы, в частности: числа вершин, числа и ве­сов дуг. В терминологии данной Лекции это либо конфигурационное, либо марги­нальное, либо смешанное управление. В тех случаях, когда принципиаль­но не удается добиться устойчивости системы в пределе, т.е. на достаточ­но большом числе шагов модели, за счет выбора ряда характеристик и удер­жания их в заданных пределах вследствие реализации управленческих решении, мож­но добиться стабильного развития процессана определен ном временном интервале.

Рекомендации тина: изменение числа вершин (ввод новых), числа н весов дуг, диапазона численных значении ряда характеристик, в которых за счет управленческих решений надо удерживать характеристики за за­данное время, - называют стабилизи­рующими страте­гиями. Они могут быть альтернативами замысла и решения.

Анализ Робертсом орграфа рис.2 показал, что даннаясистема неус­тойчива:при любом возмущении, увеличивающем значениялюбой из ха­рактеристик, энергетичес­кие мощности растут неограниченно,так жене­ограниченно ухудшается состояние окру­жающей среды.

Поскольку будем строить когнитивные модели процессов, то уточним их понятия. Когнитивной моделью будем называть ориентированный взвешенный граф -орграф, с некоторым правилом развития импульсного процесса.

Как было описано в Лекции 4, если веса дуг есть или +1, или - 1, или 0, то такой орграф называется знаковымс соответствующими весами: +1, или - 1, или 0.

Далее вспомним ряд определений, связывая их с Рис.2., которые были даны в предыдущих Лекциях 3-5.

Определение 1. О смежности двух вершин. На рис.2. смежными c вершиной C являются вершины: F, U, R. Не смежность вершин означает, что они непосредственно не воздействуют друг на друга в рассматриваемом моделируемом процессе, например, С не взаимодействует с Е.

Определение 2. Путь в орграфе - непрерывная последовательность дуг одной ори­ентации. Длина пути - число в его дуг. Из вершины Е в F имеется путь длины 3. Определения 3 и 4 - о замкнутом пути (если начинается и кончается в одной вершине орграфа) и контуре (если ни одна дуга не встречается в замкнутом пути дважды). Примером замкнутого пути является путь по вершинам Е-U-C-R-U-C-F-G-E.

Примером контура является замкнутый путь Е-U-C-F-G-E длины 5. В исследуемом орграфе помимо указанного контура длины 5 имеются еще по 1 контуру длины7 и длины 6, 3 контура длины 3 и один контур длины 2. В соответствии со сформули­рованной в Лекции 4 теоремой о знаке контура (т. Маруямы) перечисление контуров в орграфе и определение их знаков играет определяющую роль в установлении устойчивого или неустойчивого характера моделируемого процесса.

В Определении 5 говорится о том, когда контур - петля, т.е. контур длины1. Это образ простейшей обратной связи. Более сложные обратные связи охватывают вершины в контурах длины большей, чем 1.

Определение 6 Знаком пути в орграфе есть произведение знаков его дуг.

На Рис.2. знак контура Е-U-Q-E является отрицательным, а знак контура Е-U-C-F-G-E оказывается положительным. Поэтому в первом случае он ослабляет по модулю любое возмущение значений характеристик Е-U-Q, а во втором случае происходит напротив усиление подобных возмущений для значений характеристик в вершинах Е-U-C-F-G. Например, если в силу каких-то причин увеличится число предприятий - F, то все характеристики (С - энергетические мощности, G—число рабочих мест; Е- населенность; U - потребление энергии) этого контура начнут расти, и этот рост будет неограниченным, если не возникнут конкурирующие про­цессы в других контурах. Очевидно, что в 1-ом приведенном контуре будет проис­хо­дить прямо противоположный процесс, который будет ослаблять изменения характеристик Q, E, U, так как он является отрицательным. Контур R. U, С, R -положительный, следовательно, он усиливает колебания характеристик, однажды появившиеся в контуре. Аналогично ведет себя контур длины 2 -R, U, R.

Обозначение 1.Поставим в соответствиекаждой характеристике,включенной в модель,ее условный порядковый номер j, считая, что все характеристики пронуме­рованы с 1 по п, где n - число учитываемых ха­рактеристик. Вершины орграфа имеют эти же номера. т.е. отображают собой соответствующие номерам характеристики.

Обозначение 2. Для оперирования со значением характеристик вводятся для каждой из них с номером j в момент времени t функции Uj (t).

Величины Uj могут быть размерными и безразмерными.

Определение 7. Приращение введенной функции Uj (t) за единицу времени будем называть импульсом в вершине j и обозначать:

P j (t)= U j (t)- U j (t- 1). (1)

Условие З. Считаем, что импульс в вершине возникает мгновенно. Формализованное правило развития в модели импульсного про­цесса:

1. Изменения значений характеристик происходят только в дискрет­ные моменты времени t, t = 0, 1, 2,....

2. Возникший в j-й вершине импульс Р j (t) в момент времени / пере­дается за единицу времени и только в смежные вершины, т.е. появляется в смежных вершинах в момент t + 1. По дугам передаются только импульсы.

3. Импульс Р j (t) в j -й вершине передается в смежные вершины с коэффициентом усиления, равным весу дуг, соединяющих смежные верши­ны.

4. Условие линейности. Импульсы, одновременно пришедшие в i-ю вершину из смежных с нею вершин, складываются алгебраически, т.е. с учетом знаков:

P_i(t)= å Z_ji*P j (t-1), (2)

J ÎG_i,

где z_ji - вес дуги из вершины j, смежной с вершиной i; Р j (t - 1) - импульс в j-й вершине в момент t — 1; G_i- множество номеров вершин j, смежных с вершиной i, т.е. тех, из которых в i-ю вершину имеется дуга; соответст­венно

U_i(t) = U_i (t-1) + åJ ÎG_i Z_ji *P_j(t-1) (3)

Проиллюстрируем данное правило, используя орграф рис.3.3. Пере­нумеруем наши вершины так: U=>1, R^:=>2, C=>3, F=>4, G=>5, E = > 6, Q = > 7, где стрелка означает присвоение вершине данного на­именования соответствующего номера. Пусть до начала прогнозирования U_j = U_j^исх , j =1,2,..., где U_j^исх - какие-то значения соответствующих харак­теристик до моделирования.

Замечание I. Дляцелей прогноза событий с какого-то момента со­всемне обязательно знать численные значения величины U_j^исх. Если пользователей метод устраивает, то им будут выданы в качестве прогноза кривые приращений (импульсов) к характеристикам. Это уже первое пре­имущество данного подхода по сравнению с некоторыми количественны­ми моделями, в которых надо знать точные значения величин Uj. Если же пользователю надо знать величины U_j (t) для to < t < Т, то надо задавать числа U_j^исх.

Пусть в t = to = 0, где tо - начальный момент прогнозирования, в вершине С, j = 3, энергетические мощности увеличились на 1 (можно на какую угодно величину, в том числе - отрицательную), т.е. Рз (0) = 1,

Р₁ (0) = Р₂ (0) = P₄ (0) = Ps (0) = Р₆ (0) = P₇ (0). Тогда в соответствии с дан­ным правилом через один шаг импульс Рз (0) = 1 передается в вершину R в

виде(-1): Z₃₂*Рз(0) = (-1)*(+1)= -1, в вершину F: Z₃₄*Рз(0)= =(+ 1) * (+ 1) = + 1.

На одном из шагов процесса в вершине U(j = 1) воз­никнет импульс

Р₁(t) = (- 1) * P₂₁(t - 1) + (+ 1) * P₆₁(t - 1) + (+ 1) * P₄₁(t - 1).

Значение характеристики с № 1:

U₁(t) = U₁(t -1) + (- 1) * P₂₁ (t -1) + Р₆₁(t - 1) + P₄₁ (t- 1).

Задавая U_j^исх на момент t = t₀, j = 1,п, и импульсы Р_j(0), j = 1, п, ис­пользуя далее формулы (2) и (3), в которых

U_j(0)= U_j^исх + P_j(0), J=1,n, (4)

можно получить все интересующие нас значения U_j (t). К этому, собствен­но, и сводится прогноз развития моделируемого процесса.

Для облегчения расчетов и их автоматизации воспользуемся теоремой 1 (Робертс).

Величина вектора-импульса Р(t)^ТР = (P₁(t), P₂(t), ..., P_n(f)) в орграфе определяется по формуле

P(t)^TP=P(0)^TP*Z^t, (5)

где Р (0)^TP - вектор-строка; Р (0) - вектор-столбец; Z^t - t-я степень матри­цы весов данного орграфа.

Доказательство см. на с. 182 [II]. Представим выражение (1) в виде:

Uj (t) = Uj (t - 1) + Pj (t), j = 1 ,n, или в векторной форме:

U(t)=U(t-1)+P(t). (6)

Зная U (t- 1) (вектор-столбец с w-компонентами) и вектор-столбец Р(t), подсчитываемый по формуле (5), можно рассчитать вектор U(t). Тем самым определяется порядок расчетов при прогнозировании. Задавая t = 1, можно подсчитать вектор U(I): U(1) =U(0)+P (1), Р (1)^TP = Р (О)^TP * Z¹ затем U (2) = U(1) + Р (2), Р (2)^TP = Р (О)^TP * Z² и т.д. вплоть до t = Т, где T - горизонт прогнозирования. Самой трудной операцией здесь является возведение матрицы Z в степень t. Но Z^t == Z* Z^t-1, и так как на предшест­вующем шаге t - 1 уже вычисляли Z^t-1, то, сохранив Z^t-1, получаем мат­рицу Z^t как произведение двух матриц Z и Z^t-1 . Необходимые расчеты Р (t) и U (t) производят­ся быстро, ибо число вершин в когнитивной модели обычно не превышает 100, иначе она перестает отвечать своему назначению. Итак, технология прогнозирования заключается в последовательности следующих этапов:

1) построить взвешенный или знаковый орграф и определить прави­ло развития импульсного процесса;

2) задать исходные значения U_j^исх, j = 1 ,п, если требуется рассчитать полные значения Uj (t), to £ t £ Т, j = 1 ,п; в противном случае перейти к расчету импульсов в вершинах Pj (t), to £ t £ Т;

3) задать начальное возмущение в системе Р(O)^TP = (Р₁(0), Р₂(0),...), при этом компонентами вектора могут быть любые вещественные величи­ны. Начальное возмущение - это либо прогнозируемое в окружающей среде событие, влекущее за собой импульс Р (0), либо результатреализа­ции управленческого решения;

4) задать горизонт прогнозирования – Т,

5) сформулировать требования к форме представления результатов (графики, таблицы, наборы и последовательности цифр), а также требова­ния к разрезам времени (t) (номера шагов моделирования, на которых надо выдавать прогнозные величины, перечень характеристик для предъявле­ния пользователю на отдельных шагах моделирования).

Главные трудности связаны с построением орграфа, определением знаков и/или весов дуг, а также с выработкой правил развития импульсно­го процесса, отражающих суть моделируемых процессов.

Порядок прогнозирования, изложенный выше, обеспечивает просто­ту машинной реализации, однако у него имеется пара уязвимых мест - тождественность временных квантов и условие линейности:

а) время передачи импульсов между всеми вершинами одинаково и равно некой условной единице, хотя в действительности оно может быть разным и не обязательно целым числом; б) воздействие нескольких характеристик на одну сводится к аддитивной сумме импульсов (хотя уровень некоторых переменных может зависеть и от величины воздействующих переменных) и их приращений - импульсов из предшествующего цикла.

Предлагается следующий способ преодоления первого из недостатков.

Устанавливаются реаль­ные возможные сроки передачи возмущений-импульсов между всеми па­рами вершин i и j, смежных между собой. t_ij, i =1,п, j = 1,п. Среди таких пар могут быть и вершины с одинаковыми номерами, т.е. в отдельных вершинах могут бытьпетли: дуга выходит и входит в одну и ту же вершину. Определяется t₀ - наибольший общий делитель чисел t_ij, на ко­торый каждое из них делится нацело (может быть, с какой-то заданной точностью, т.е. остаток от деления не превышает заданного малого числа). Величина t₀ принимается за величину одного шага модели. Получаемые числа

t_{ij /}t₀ = l_ij, (7)

используются так. Между вершинами i и j вставляются (l_ij - 1) фиктивных вершин и дуг между ними той же ориентации и знака, что и дуга между i и j до преобразования. Если орграф, взвешенный и |Z_ij| ¹1, то вес каждой но­вой искусственной дуги между вершинами i и j приравнивается величине

(Z_ij)^1/a , где a =l_ij . (8)

В результате формально число дуг в преобразованном орграфе рас­тет, но время передачи импульсов между новыми вершинами по-прежнему равно одной условной единице. Между разными вершинами исходного орграфа время прохождения импульсов будет разным: оно возрастает там, где введены фиктивные вершины.

Устранение второго слабого места более проблематично. Избавление от аддитивного сложения(l_ij импульсов приводит к резкому усложнению модели. Принципи­ально это возможно, если, например, воздействие между любой парой вершин можно представить в виде некоторой неаддитивной функции. Но тогда получится обычная количественная модель, что попросту лишает преимущество когнитивного подхода. Это, в сущности, и показывает границу его применимости.

В принципе допускается единственное усложнение, которое представляется целесообразным при прогнозе тенденций развития событий, т.е., когда важны знаки прира­щений изучаемых переменных, а не их точные значения, - в процессе замены зна­ков на веса – Z_ij. Введение на дугах весов вещественных чисел вместо зна­ков -следующий шаг уточнения модели. Ниже приводится методика, которая по­зволяет вычислить веса дуг при наличии уверенно заданных знаков дуг. Расчеты ведутся на основе имеющейся по данной проблеме статистики.

Схема методики расчета матрицы весов Z = (Z_ij. i = 1 , n, j = 1 ,n)

1. Создается знаковый орграф с матрицей весов (x_ij), где x_ij, либо О, либо + 1, либо - 1, j = 1,п, i = 1 ,п.

2. Собирается статистика: динамические ряды значений характери­стик Uj* (t), Т^P < t < to, в прошлом, где Т^P - такой момент в прошлом, что число точек в динамическом ряду каждой характеристики не меньше не­обходимого их числа М. Число М определяется из нижеследующих усло­вий

3. Задается достаточно малое положительное число e, определяющее точность расчетов весов.

4. Решается задача: найти вещественные числа Z_ij, ( i = 1,n, j =1,п, такие, чтобы

åå( Z_ij - x_ij)² ® min (9)

при ограничениях

U_j (t) - e £ U_j(t) £ U_j^* (t) + e, j ⁼ 1 , n, t = 1 , Мо, (10)

где U(t)=U(t-l)+P(0)Z^t, (11)

U_j (0) = U_j* (T^P) + P_j (0), j = 1, n, (12)

P, (0) = U_j* (Т^P + 1) - U_j* (T^P), j =1,n. (13)

M₀ - такое число точек в общей выборке данных о U_j* (t) в прошлом, которое позволит решить данную задачу, Uj (t) - расчетные, a Uj* (t) - рет­роспективные значения характеристик с U_j (0).

Замысел решения так поставленной задачи состоит в следующем:

на основании статистики о поведении характеристик в прошлом на отрезке [Т^P , tо] и на­личия знаков дуг Х_ij между вершинами построенного знакового орграфа необходимо найти такие веса Z_ij - вещественные числа (могут быть отлич­ными от + 1 и - 1), сумма квадратов отклонений которых от целочислен­ных весов +1 или - 1 (x_ij) была бы наименьшей [см. условие (9)]. Минимальные отклонения будут получены, если Z_ij = Х_ij для всех i и j. Любое отклонение веса Z_ij от + 1 или - 1, отображающих знак дуги Х_ij, как в сторону увеличения, так и в сторону уменьшения от модуля ½x_ij½ дает ненулевой вклад в сумму-функционал (9). Изменение веса Z_ij по сравнению с величиной Х_ij меняет степень матрицы искомых чисел Z для всех t =1, М₀. В свою очередь это меняет по сравнению с расчетами на основе матрицы X^t = (x_ij, i =1, n, j = 1,п) величины расчетных значений Uj (t) характеристик. Требование (10) заставляет расчетные значения Uj (t) в каждый момент времени в прошлом (t = 1 ,Мо) отличаться от наблюдаемых значений Uj* (t) в прошлом не более чем на величину e- достаточно малое положительное число. Тем самым веса Z_ij должны быть подобраны так, чтобы расчетные значения U_j (t) практически совпадали с зарегистрированными в статисти­ке.

Zij1/a, где а= lij,

(8)

Как правило, начальный импульс Р(0) в прошлом точноне известен. Расчеты следует начинать с пре­д­­по­ложения, что компоненты вектора Р (0) равны разнице фактических значений U_j * (T^P + 1) - U_j* (T^P) для всех j с учетом условия (12). Этим обстоятельством может быть внесена серьезная ошибка в оценку весов. Фактически полученные веса являются функцией величины Р(0) в форму­ле (11). Меняя Р(0), не считаясь одновременно с условием (12), можно по­лучать разные значения весов z_ij как функциюР (О):z_ij = z_ij(Р(0)). Критерием правильности подбора начального импульсаР (0) будет служить уменьшение значений функционала (9)

å å (z_ij(Р(0)) - x_ij)²

J i

Вычисление двойственных оценок к условию (11) покажет,какие изкомпонентов вектора Р(0) и на какую величину следуетизменять, чтобы уменьшать значения (9), т.е.

минимизировать å å (z_ij(Р(0)) - x_ij)²

J i

и когда этот процесс должен быть остановлен.

Таким образом, задача расчета весов дуг на основе знаков имеет, с точки зрения авторов предложенной методики, вид регулярной, полностью формализованной процедуры. К сожалению, ее решение тpебуeт достаточно сложных и трудоемких машинных программ.

5. Имеющаяся статистика разбивается на две части: обучающую и контрольную. В обучающую выборку включают М₀ точек из каждого динамического ряда Uj* (t), t £ to. или (при неравномерной плотности рядов -разном числе точек наблюдения для разных характеристик) такое их чис­ло, чтобы в наименее плотном динамическом рядуих было М₀ .

М₀ ³ n, где n- число вершин знакового орграфа. В контрольнойвыборке также должно быть не менее nнаблюдений за каждой характеристикой.

Примечание. Последнее требование вызвано тем, что в орграфе с n вершинами наибольшая длина замкнутого простого пути, проходящего по всем вершинам, не может быть больше п. Возникнув в одной вершине, импульс через n шагов вернется в нее же, если есть простой путь.

Благодаря наличию n точек контроля за Uj{t}, 1 £ t £ М₀, будутпроверены веса всех дуг, входящих в такой путь. Доказано, что если естьполный замкнутый путь, то в нем всегда можно выделить простой замкнутый путь длины n.

Рассчитав веса на обучающей выборке, приступают к проверкеих правильности, сравнивая расчетные значения Uj{t} и полученные в резуль­тате наблюдения Uj* (t) и контрольной выборке.

Если U_j^*(t) - e £ U_j(t) < U_j^*(t) + e, то значениявесов верные.Впро­тивном случае расширяют обучающую выборку за счет точекиз контроль­ной выборки, меняют Р(0) и повторяют расчеты.

Если орграф отражает исследуемый процесс, и знаки определены верно,то подобная процедура должна рано или поздно завершиться. В случае, когда обучающая выборка совпадает со всей выборкой, данный орграф не может считаться достаточно корректной моделью.