Дерево вероятностей как метод оценки зависимости денежных потоков по годам проекта.
Метод дерева вероятностей имеет целью оценку вероятностного распределения будущего потока по результатам предыдущего года. Рис. 8.3 показывает дерево вероятностей для 2-летнего проекта. В момент 0 дерево вероятностей показывает лучшую оценку того, что может произойти в будущем с учетом развития в предыдущие годы. В первый год результат чистого денежного потока не зависит от того, что было прежде, поэтому вероятности р1 и р2 называются исходными. р1 + р2 = 1. В год 2 вероятности зависят от предыдущего результата по чистому денежному потоку и носят название условных. Вероятность появления определенной последовательности денежных потоков называется совместной вероятностью. Совместная вероятность является результатом исходной и условной вероятностей и численно равна их произведению.
Метод дерева вероятности исходит из следующей схемы действий:
1) рассчитываются для каждого года функционирования проекта условные и исходные вероятности;
2) рассчитывается значение чистого денежного потока по каждой ветви, например:
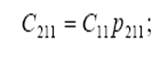
3) рассчитывается значение чистого дисконтированного дохода по каждой ветви дерева вероятностей, например, по верхней ветви дерева, представленного на рис. 8.3:
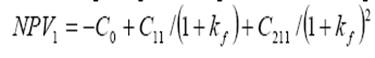
В качестве ставки дисконтирования принимается безрисковая ставка процента на рынке;
4) рассчитывается ожидаемое значение ЛТТ как средневзвешенное, где весами выступают совместные вероятности. Например, для 2-летнего проекта на рис. 8.3:
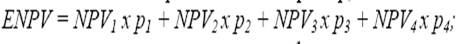
5) рассчитывается стандартное отклонение по формуле
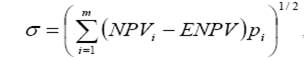 ,
,
где pi — совместная вероятность.
Интерпретация результатов
При принятии инвестиционного решения в условиях риска важно ответить на два вопроса:
• какова степень риска;
• генерирует ли проект положительное значение чистого дисконти-рованного дохода (NPV).
Эти вопросы решаются в вероятностном анализе следующим образом:
Если вероятностное распределение NPV нормальное, то можно оценить вероятность получения нулевого значения NPV. В рассмотренном выше численном примере ожидаемое значение чистого дисконтированного дохода (ENPV) равно 268 млн. руб. Пронормируем это значение, разделив на стандартное отклонение по формуле z =(Х - ENPV)/ а, где х = 0. В результате найдем степень отклонения, выраженную в числе стандартных отклонений: z = (0 - 268) /206 = - 1,3, т.е. нулевое значение NPV находится на расстоянии 1,3 стандартного отклонения влево от математического ожидания возможных значений чистого дисконтированного дохода. Таблица нормального распределения (см. табл. 6 Приложения 2) позволит найти для значения -1,3 оценку вероятности, она составляет 0,0968. Это вероятность того, что значение NPV проекта будет меньше или равно нулю. Соответственно с вероятностью 90,32% (1 - 0,0968) можно утверждать, что проект генерирует положительное значение NPV.
