Неоклассическая теория финансов 2 страница

Доу не дал конкретного количественного инструментария для по­добной оценки; более того, его в большей степени привлекали система­тический анализ и обобщение динамики цен, нежели их предсказание. Тем не менее его аналитические обзоры пользовались исключительной популярностью, а его последователи утверждали, что с помощью подоб­ного анализа можно делать и прогнозные оценки.

Все же наиболее существенный вклад Доу в разработку теоретиче­ских аспектов финансовой науки связан с формулированием идеи ин­декса на рынке ценных бумаг, получившего в дальнейшем название ин­декса Доу-Джонса. Это была первая попытка конструирования некое­го обобщающего индикатора фондового рынка, усредненной характери­стики, отражающей происходящие на нем тенденции. Любопытно отметить, что с тех пор появились и другие индексы с более замыслова­тыми алгоритмами исчисления, однако до сих пор индекс Доу-Джонса остается наиболее известным и авторитетным индикатором фондового рынка.

История появления индекса такова. В 1882 г. Доу начал публико­вать перечень компаний, чьи акции в наибольших объемах торговались на бирже. Уже тогда Доу не исключал возможности периодического из­менения этого перечня, что предопределялось как неизбежными спада­ми/подъемами деятельности зарегистрированных на бирже компаний, так и ростом числа эмитентов и участников рынка (любопытно отме­тить в связи с этим^что если в начале 80-х гг. XIX в. среднедневной объ­ем торгов на Нью-Йоркской фондовой бирже составлял около 250 тыс. акций, то 30 лет спустя он превысил 100 млн акций).

Собственно индекс Доу-Джонса, построенный по данным текуще­го перечня наиболее торгуемых акций, впервые появился 3 июля 1884 г. в газете Afternoon News Letter; он характеризовал динамику цен закры­тия акций одиннадцати компаний (девять железнодорожных и две про­мышленных). С 1886 г. индекс рассчитывался уже по акциям двенадца­ти промышленных компаний, в число которых вошли American Cotton Oil, American Sugar, American Tobacco, Chicago Gas, Distilling and Cattle Feeding, General Electric, Laclede Gas, National Lead, North American, Ten­nessee Coal & Iron, US Leather (preferred), US Rubber. С 1928 г. и по на­стоящее время индекс Доу-Джонса рассчитывается по данным о дина­мике акций тридцати крупнейших компаний, в связи с этим любопытно отметить, что из вышеприведенного первоначального перечня только General Electric продолжает входить в него. Одно из примечательных включений в список в последние годы — компания Microsoft, которая,

будучи создана всего лишь в 1975 г., постоянно отличалась наибольшей динамичностью в своем развитии и на момент включения в список (но­ябрь 1999 г.) стала крупнейшей компанией в мире по капитализации рынка акций¹.

Резюмируя, можно утверждать, что Доу был убежденным сторонни­ком ведения бизнеса на фондовом рынке и еще в 1882 г. высказал мысль о том, что этот рынок будет со временем наиболее спекулятивным и привлекательным для бизнесменов. Разработки Доу, не будучи фор­мализованными, были чрезвычайно глубоки по своей сущности и в дальнейшем использовались в различных направлениях. С одной сто­роны, предложенная и реализованная Доу практика систематического и тщательного анализа динамики цен, по сути, дала начало формирова­нию технократического подхода к оценке финансовых активов, офор­мившегося впоследствии в так называемый технический анализ. С дру­гой стороны, неоднократно высказывавшаяся им и его последователями мысль о самодостаточности фондового рынка привела позднее (в 1960-е гг.) к развитию новых подходов к оцениванию — фундамента­листского и теории «ходьба наугад»; в той или иной степени все эти подходы связаны с пониманием гипотез эффективности рынка капита­ла (суть гипотез будет рассмотрена ниже).

Теория «ходьба наугад»- (Random Walk Theory). В 1900 г., т. е. два десятилетия спустя после высказанной Доу идеи о возможности про­гнозирования поведения фондового рынка, молодой французский мате­матик Луи Башелье (1870-1946) завершил в Сорбонне свою доктор­скую диссертацию «Теория спекуляции», в которой попытался с помо­щью математического аппарата дать объяснение поведению цен акций на французском фондовом рынке. В своей работе, увидевшей свет в 1900 г., Башелье пришел к мрачному выводу, что динамика цен на фондовой бирже никогда не будет точной наукой. Хотя Башелье, по су­ти, выступил оппонентом Доу, его заслуги в развитии теории финансов неоспоримы, поскольку именно ему принадлежит идея приложения стохастических моделей к анализу поведения цен на рынке капитала.

¹ По данным влиятельной газеты «Financial Times», ежегодно составляющей рей­тинг 500 крупнейших компаний мира, в 2008 г. на первом месте оказалась «Exxon Mobil» (США) с рыночной капитализацией 452,5 млрд долл. Следующие места в пятер­ке заняли: «PetroChina» (Китай, 424 млрд долл.), «General Electric» (США, 369,6 млрд долл.), «Газпром» (Россия, 299,8 млрд долл.), «China Mobile» (Гонконг, 298,1 млрд долл.). Совокупная капитализация 500 крупнейших компаний мира в 2008 г. составила 26,83 трлн долл. В рейтинг вошли 13 российских компаний (в 2007 г. — 8, в 2006 г. — 6): «Газпром» (299,8 млрд долл.), «Роснефть» (95,9 млрд долл.), «ЛУКОЙЛ» (72,7 млрд долл.), «Сбербанк» (69,6 млрд долл.), «Норильский никель» (54,0 млрд долл.), РАО «ЕЭС России» (44,5 млрд долл.), «Сургутнефтегаз» (39,4 млрд долл.), «Мобильные те­лесистемы» (25,5 млрд долл.), «Новатэк» (24,8 млрд долл.), ВТБ (24,5 млрд долл.), НЛМК (24,3 млрд долл.), «Северсталь» (22,8 млрд долл.), «Вымпелком» (21,5 млрд долл.). Совокупная капитализация российских компаний из рейтинга «Financial Times» оценена в 819,54 млрд долл. С 2007 г. «Газпром» является крупнейшей компанией в Ев-

ропе.

Раздел VII. Финансовая наука в исторической ретроспективе

Глава 27. Эволюция финансовой науки

Башелье был «чистым» ученым, и свидетельств о том, использовал ли он на практике свои рекомендации, нет. Что касается научной значи­мости, то работа Башелье была исключительно новаторской, поскольку в ней он не только реализовал идею приложения стохастических про­цессов к анализу поведения цен на рынке капитала¹, но и сделал попыт­ку теоретического обоснования оценки таких финансовых инструмен­тов, как опционы и фьючерсы [Bernstein, р. 18]. Любопытно, что все это делалось французским ученым лишь с одной целью — объяснить, поче­му цены на рынках капитала не поддаются обоснованному прогнозиро­ванию, а его вывод был поистине безжалостным и в известном смысле пессимистичным: «... текущая флуктуация (т. е. изменение цен на фон­довой бирже. — В. К.) есть функция, но она определяется не только флуктуациями, имевшими место ранее, но также и текущим состоянием рынка. Эти флуктуации зависят от бесчисленного числа факторов, а по­тому попытка их математического прогнозирования бесполезна. ...Ди­намика (цен. - В. К.) на фондовой бирже никогда не будет точной нау­кой» [цит.: Bernstein, р. 19]. Несмотря на столь мрачный вывод, Баше­лье вместе с тем поставил перед собой весьма амбициозную цель — предложить формулу, выражающую вероятность появления рыночных флуктуации. Таким образом, основная идея исследования Башелье мо­жет быть выражена следующим тезисом: цены на финансовом рынке не поддаются точному прогнозу, возможны лишь оценки в терминах веро­ятности.

Историки не без основания полагают, что исследование Башелье значительно обогнало свое время — лишь в 1950-х гг. идеи француза были развиты в работах выдающегося статистика Мориса Кендэлла. Отчасти этим объясняется тот факт, что оно осталось практически неза­меченным, равно как и сам ученый не стал знаменитым и лишь с трудом сумел устроиться на работу в университет провинциального Безансона. Более того, собственное отношение исследователя к полученным ре­зультатам было неочевидным — Башелье рассматривал свои модели не с позиции их практического приложения, но как иллюстрацию их инст­рументальных возможностей, поскольку финансовые рынки, по его мнению, давали богатейший статистический материал для занятий со студентами, специализирующимися в области теории вероятностей и математической статистики. Иными словами, осознанно или нет, но французский ученый стоял, по сути, у истоков направления, оформив­шегося впоследствии в теорию «ходьба наугад». Однако лишь шесть де­сятилетий спустя идеи и модели Башелье оказались востребованными практиками.

В 1954 г. Джимми Сэвидж, математик из университета Чикаго, случайно обнаружил в университетской библиотеке небольшую книж-

¹ Историки отмечают, что статистическая теория броуновского движения и тео­рия флуктуации позднее были развиты Альбертом Эйнштейном.

ку Башелье о спекуляциях и инвестициях, изданную в 1914 г. Ее со­держание настолько поразило ученого, что он начал наводить справки о «неизвестном» Башелье среди своих коллег; оказалось, что никто из них ничего не слышал о французе и его работах. Заинтригованный рассказом Сэвиджа, Пол Самуэльсон (род. 1915) также подключился к розыскам. В то время он работал в известной кузнице научных кад­ров — Массачусетском технологическом институте; в библиотеке это­го института ему удалось обнаружить копию диссертации Башелье. Мнение Самуэльсона о работе также было весьма высоким: «Кажется, Башелье мыслил однобоко, но каков «бок»!». С легкой руки Самуэль­сона весьма приглянувшийся ему термин «спекуляция» с тех пор прочно вошел в число базовых терминов теории финансов [Bernstein, р. 23].

Фундаменталистский подход. После смерти Доу и забвения раз­работок Башелье в первой четверти XX в. теоретические исследования по фондовому рынку практически не проводились, хотя французом в отличие от Доу уже был дан определенный научный инструментарий. Казалось бы, научный мир и практики много потеряли в связи с тем, что своевременно не обратили внимание на идеи Башелье. Однако, по мне­нию Питера Бернстайна, даже если бы работы французского ученого получили признание в научной среде в момент их опубликования, вряд ли они использовались бы практиками. Одна из причин состояла в том, что в те годы люди, реально контролировавшие финансы, практически не обращали внимания на рынки капитала; именно такая ситуация бы­ла характерна, например, в США.

В отличие от практиков, больше полагавшихся на опыт и интуицию, ученые пытались вникнуть в суть процессов ценообразования. Идея о том, что стоимость товара зависит не столько от вложенного в него труда, сколько от потенциальных выгод в связи с обладанием им, была воспринята в том числе и учеными, работавшими в области теории фи­нансов. В числе первых исследователей в области теории оценивания на фондовом рынке в рамках фундаменталистского подхода был выпу­скник Гарвардского университета Джон Уильяме (1902—1989)¹, кото­рый в своей докторской диссертации², написанной в 1937 г., предложил в качестве одного из инструментов для работы на рынке ценных бумаг

' См. [Van Home, Wachowicz, p. 81].

² Основные положения диссертации были опубликованы Уильямсом в 1938 г. в издательстве Гарвардского университета в книге «Теория инвестиционной ценно­сти» (любопытно отметить, что эту работу отказались опубликовать издательства Macmillan и McGrow Hill, сославшись на то, что в ней много математики, а Гарвард при­нял книгу к публикации лишь с условием, что автор возместит часть расходов). В 1940 г. в Гарварде по материалам монографии состоялась защита докторской диссер­тации (Philosophy Doctor, PhD). Комиссия, принимавшая у соискателя устный экза­мен, а это одна из составных частей процесса защиты диссертации, состояла из весьма авторитетных специалистов: Йозеф Шумпетер, Василий Леонтьев и Элвин Хансен.

Раздел VII. Финансовая наука в исторической ретроспективе

Глава 27. Эволюция финансовой науки

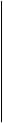
модель оценки финансовых активов¹, построенную на дисконтирова­нии дивидендов, выплачиваемых в денежной форме (Dividend Discount Model, DDM):

где V_t — теоретическая (внутренняя) стоимость обыкновенной акции;

Dk — выплаченный дивиденд в k-м периоде;

г — ставка дисконтирования.

Идея Уильямса была проста: любая вещь стоит ровно столько, во что может быть оценена извлекаемая из нее польза. Поскольку основ­ным продуктом, генерируемым акцией, и «потребляемым» ее владель­цем, в конечном счете является поток дивидендов, оценивать акцию следует именно по дивидендам. Кроме того, необходимо учесть фактор времени. Отсюда и возникает модель (27.1). Эта модель позволяла каж­дому инвестору получить формальную оценку теоретической, или внутренней, стоимости акции, с которой уже можно было сравнить ее текущую цену; по результатам сравнения могло быть принято решение в отношении купли-продажи актива. Уильяме не затрагивал вопросы портфельных инвестиций; эта проблема будет рассмотрена позднее Гар­ри Марковицем.

Уместно заметить, что модель Уильямса подвергалась критике как теоретиками, так и инвесторами-практиками. Первые утверждали, что модель не может описать все возможные ситуации, а результаты про­гнозирования, полученные с ее помощью, могут не согласовываться с теоретическими выводами и практическими действиями; вторые ука­зывали на невозможность прогнозирования бесконечного потока диви­дендов. Так, в 1957 г. Дэвид Дюран опубликовал статью, в которой он подверг сомнению теоретическую обоснованность модели Уильямса (см. [Durand]). Для доказательства он привел в пример известный пе­тербургский парадокс, сформулированный Даниилом Бернулли

' Заметим, что собственно идея дисконтирования естественно не является изобре­тением Уильямса. Таблицы сложных процентов были впервые разработаны и опубли­кованы математиками Яном Тренченом и Симоном Стевином (1548—1620) соответст­венно в 1558 и 1582 гг., причем именно Стевин как раз и высказал идею о возможности использования чистой дисконтированной стоимости для оценки финансовых инвести­ций [The History of Accounting, p. 208]. Однако лишь в конце XIX в. эта идея получила активное развитие в работах экономистов. Так, в 1887 г. американский инженер А. Вел­лингтон опубликовал работу «Экономическая теория размещения железных дорог», в которой предложил подход к обоснованию целесообразности строительства новой дороги на основе сопоставления дисконтированных значений прогнозных притоков и оттоков денежных средств. В 1891 г. английский бухгалтер Френсис Мор впервые предложил оценивать гудвилл исходя из генерируемых им дополнительных доходов [Кат, р. 401—403]. Идея дисконтирования активно использовалась А. Маршаллом (1842—1924) и И. Фишером (1867—1947) при изложении логики и техники бюджети­рования капиталовложений и оценки инвестиционных альтернатив.

(1700—1782) еще в 1738 г. на заседании в Императорской Академии на­ук в Санкт-Петербурге.

Суть парадокса в следующем. Предположим, что крупье подбрасы­вает монету и предлагает следующие условия: если орел появится в пер­вой попытке, то участник игры получит 1 руб., если не в первой, а лишь во второй, то 2 руб., если не в первых двух, а лишь в третьей, то 4 руб., если не в первых трех, а лишь в четвертой, то 8 руб. и т. д. Иными слова­ми, с каждой очередной попыткой сумма возможного выигрыша удваи­вается. Спрашивается, какую цену крупье может запросить за участие в этой игре. Поскольку монета «правильная» (т. е. она не является де­фектной, а потому игра честная), выпадение орла или решки равноверо­ятно и, кроме того, исходы в попытках независимы. Теоретически игра может длиться бесконечно долго. Несложно подсчитать математическое ожидание выигрыша E(S) — в условиях честной игры именно E(S) и бу­дет представлять собой цену, требуемую за участие в игре. Вероятность появления первого события '/г; второго — 'Д; третьего — Vs ^{и т}- Д- По­этому:

E(S) - 1- »/а + 2 • (¹/₂)² + 4 • (У₂)³ + 8 • (»/,)< + ... =

= 72+¹/2 + ¹/2 + ¹/2 + ... = +⁰⁰-

Иными словами, в условиях честной игры потенциальный участник должен заплатить за возможность участия в ней бесконечно большую сумму денег. Ясно, что желающих включиться в игру на таких условиях не сыщется. С другой стороны, понятно, что, если условия азартной иг­ры не являются с очевидностью нечестными, всегда находятся потенци­альные участники — все дело в запрашиваемой цене и в установлении критерия, приемлемого для организаторов и участников игры. Отсюда напрашивается вывод о том, что потенциальные участники любой азартной игры (а азартный бизнес, как известно, процветает, несмотря на огромные налоги) принимают во внимание не только формальные суммовые показатели — для них существенны какие-то другие, возмож­но неформализуемые критерии.

Понимание этого обстоятельства как раз и помогает найти некото­рые возможные варианты поведения участников описанной Бернулли игры. В частности, парадокс может быть разрешен, если согласиться с утверждением, что когда речь идет о бесконечном ряде стоимостных величин, потенциальный участник оценивает не столько собственно суммовые величины, сколько ожидаемые полезности, представляющие собой некоторую функцию от суммовой величины. Смысл данного предположения понятен: полезность (т. е. ценность) любого ожидаемо­го рубля будет ниже полезности предшествовавшего рубля (более на­глядный пример: если человек голоден, любой кусок хлеба для него практически бесценен, но по мере насыщения ценность вновь предла­гаемого куска начинает довольно быстро убывать). Итак, с течением времени полезность единицы ожидаемой суммовой величины снижает­ся. Предположим, что зависимость полезности от суммовой величины

876 Раздел VII. Финансовая наука в исторической ретроспективе

Глава 27. Эволюция финансовой науки 877

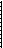
описывается квадратичной функцией: U = 4S. Можно рассчитать мате­матическое ожидание полезности в рассматриваемой игре:

E(S) = 41 ■ (W + ^ ■ Oh)² + V4 • (V2)³ + V8 • (V2)⁴ +... -

= q² + q^A + q⁴ + q^s + ...

42 где q = -P-.

Домножив обе части уравнения на q и вычтя полученное уравнение из первого, получим:

Отсюда находим: S = U² = 1,71² = 2,92 руб.

Иными словами, если принимать решение с учетом функции полез­ности, то потенциальный участник с такой функцией полезности будет готов заплатить 2,92 руб. за возможность участия в игре. Парадокс раз­решен, но лишь отчасти. Дело в том, что потенциальные участники игры могут по-разному определять устраивающую их функцию полезности. А потому очевиден вывод: в условиях неопределенности нельзя пред­сказать поведение потенциальных участников, поскольку не известны их функции полезности. Отсюда и возникает идея классификации уча­стников в контексте их отношения к риску. Дюран утверждал, что на практике именно это и имеет место: осоз­нанно или нет, но потенциальный инвестор не ограничивается фор­мальной оценкой ожидаемых к получению величин, он по-разному от­носится к риску, а потому модель Уильямса не может рассматриваться как теоретически обоснованная и безупречная. Иными словами, ориен­тироваться лишь на дивиденды, распространять сложившуюся их дина­мику на будущее (а именно эта идея использована, например, в широко известной модели Гордона) нельзя — это может привести к разраста­нию финансового пузыря (в частности, признаки пузыря проявляются в том, что значение отношения текущей рыночной цены акции к теку­щему доходу на акцию так называемый индикатор Р/Е становится ано­мально большим). Вместе с тем понятно, что рассуждения Дюрана име­ют чисто теоретическое значение, а введение в рассмотрение функций полезности никак не делает инвестиционный анализ на основе форма­лизованных моделей более практичным.

Разработки Уильямса представляли собой лишь первые конкрет­ные шаги в развитии инвестиционного анализа, а модель (27.1) вошла в историю финансовой науки в связке с фундаменталистским подхо­дом. Можно назвать две основные причины: во-первых, модель Уиль­ямса в наиболее акцентированном виде выражает идею движения в це­нообразовании от будущего к настоящему; во-вторых, ей присуща оче­видная наглядность и простота в реализации (правда, кажущаяся). В целом же еще в начале XX в. развитие количественных методов обос­нования решений не было сверхдинамичным.

Ситуация, которую можно охарактеризовать как вялотекущий про­цесс исследования рыночных тенденций, начала меняться, причем кар­динальным образом, после знаменитого кризиса в конце 20-х — начале 30-х гг. XX в., вошедшего в историю как Великая депрессия. Жертвами кризиса стали многие бизнесмены; в их числе оказалось и семейство Коулзов. Альфред Коулз (1891—1985) после окончания Йельского уни­верситета начал работать репортером, но вскорости заболел туберкуле­зом и был направлен на излечение в известное курортное местечко Ко­лорадо-Спрингс, где и провел около десяти лет.

Семейство Коулзов было весьма состоятельным — глава семьи вла­дел значительным пакетом акций и одновременно входил в число топ-менеджеров крупной компании. Не желая терять время попусту, Альфред решил помогать своему отцу в вопросах управления финанса­ми. Он выписал множество специализированных журналов, однако спустя некоторое время пришел к выводу, что их противоречивыми ре­комендациями вряд ли можно пользоваться. Имея целью отобрать одно издание, рекомендациям которого в отношении рынков капитала мож­но было бы следовать, он в течение четырех лет анализировал и систе­матизировал данные из более чем двух десятков журналов и файлов. Это были годы, когда фондовый рынок в США испытал наибольший бум и жуткое падение, причем для подавляющего числа аналитиков ка­тастрофа на финансовом рынке оказалась полной неожиданностью.

Пытаясь найти ответ на вопрос о том, можно ли прогнозировать це­ны на фондовом рынке и если да, то каким образом, и ощущая недоста­ток знаний в этой области, Коулз обратился за помощью к своему другу биохимику Чарльзу Бойсвейну, который был пациентом пансионата и одновременно возглавлял в нем исследовательский отдел по пробле­мам туберкулеза. Бойсвейн свел Коулза с Гарольдом Дэвисом, профес­сором математики в Университете Индианы, с которым Коулз обсудил возможность и сделал с помощью машины Холлерита (одна из первых моделей концерна IBM) пробные прогнозные расчеты на основе множе­ственного уравнения регрессии. Кроме того, Дэвис порекомендовал Ко-улзу обратиться в Эконометрическое общество, намекнув на то обстоя­тельство, что общество испытывает финансовые затруднения и не мо­жет найти денег на публикацию результатов своих исследований¹.

Коулз немедленно связался с президентом Общества известным про­фессором Ирвингом Фишером (1867—1947) и предложил профинансиро­вать публикацию журнала Общества. После непродолжительных перего-

¹ Эконометрическое общество было создано в 1929 г. Его первый президент — Й. Шумпетер (1883—1950); И. Фишер также был президентом этого общества, воспи­тавшего плеяду выдающихся ученых, многие из которых в дальнейшем были награжде­ны Нобелевской премией: Дж. Тобин (1918—2002), Г. Марковиц (род. 1927) и др. С 1933 г. Общество выпускает знаменитый журнал «Эконометрика», в первых выпус­ках которого были опубликованы и статьи Коулза по проблемам прогнозирования на фондовом рынке.

Раздел VII. Финансовая наука в исторической ретроспективе

Глава 27. Эволюция финансовой науки

воров стороны пришли к обоюдному согласию; более того, в 1932 г. Коулз основал и профинансировал деятельность так называемой Комиссии Коул-за по исследованиям в экономике. В эту Комиссию вошли многие члены Эконометрического общества, а поставленная Коулзом перед Комиссией цель как раз и состояла в том, чтобы разработать теоретические рекомен­дации в отношении финансовых рынков. Коулз был не только замечатель­ным организатором, выражаясь по-современному — менеджером, но и дельным ученым — он систематизировал и обобщил многолетние дан­ные специализированных агентств о прогнозах цен на рынке капитала и их рекомендации в отношении управления финансовыми инвестициями и опубликовал по результатам своего исследования ряд статей.

Новые подходы к теории оценивания на рынке ценных бумаг, кото­рые пытались разработать ученые Комиссии Коулза, в значительной степени носили теоретизированный характер, а потому в течение дли­тельного времени не были востребованы практиками. Более того, исто­рики отмечают, что собственно финансовый рынок не слишком интере­совал экономистов; не случайно после Башелье к этому сегменту эконо­мики обращались лишь спорадически, да и то как к источнику огром­ных объемов статистических данных. В 1934 г. Холбрук Вёкинг, исследователь из Стэндфордского университета, опубликовал статью по методологии анализа приростных значений элементов рядов дина­мики, исходным материалом для которой послужили данные о ценах на финансовых рынках [Working]. Он выявил любопытную закономер­ность: если собственно динамика цен обнаруживала некоторый набор краткосрочных трендов, то весь массив приростных значений цен вел себя абсолютно случайным образом. Иными словами, подтвердилась гипотеза Башелье о невозможности формализованного прогнозирова­ния на финансовом рынке. Двадцатью годами позднее английский ста­тистик М. Кендэлл также попытался найти формализованное решение проблемы, сформулированной Ч. Доу — разработать инструментарий для отграничения долгосрочных трендов от краткосрочных флуктуа­ции при оценке рядов динамики. Вновь использовались данные о дина­мике цен на различных рынках¹, и в очередной раз гипотеза о возмож­ности прогнозирования не подтвердилась. Вывод ученого таков: «Памя­ти фондовой биржи, по-видимому, хватает менее, чем на неделю. Инве­сторы, возможно, могут делать деньги на фондовой бирже, но, очевидно, не благодаря отслеживанию ценовой динамики и ориентации на кажу­щуюся тенденцию. Вместе с тем непохоже, что мои слова или приве­денные аргументы разрушат иллюзию того, что пришедший на рынок инвестор может обыграть его, а потому пусть он действует на рынке

¹ Обработанный Кендэллом массив был огромен — в частности, он включал поме­сячные данные Чикагской товарной биржи за период с 1883 по 1934 г. и Нью-Йоркской товарной биржи за период с 1816 по 1951 г., понедельные данные по группам акций за период с 1928 по 1938 г. и т. д.

в соответствии со своими собственными размышлениями и инструмен­тами» [Kendall]. С приведенным выводом в той или иной форме позд­нее соглашались многие видные специалисты, в том числе и проводив­шие исследования в контексте фундаменталистского подхода. Иными словами, экономические процессы, если и поддаются некоторой форма­лизации, то лишь с существенными оговорками и в определенных пре­делах¹.

Подчеркнем, что исследования Башелье, Коулза, Кендэлла, Уиль-ямса и других ученых носили, можно сказать, формализованный, мате-матико-статистический характер. Однако известно, что в экономике ог­ромную роль играет фактор субъективности; следование этому очевид­ному тезису как раз и предостерегает от безоглядной веры в формализо­ванные модели и методы. Кроме того, практикующие участники финансового рынка всегда с определенным предубеждением относятся к рекомендациям теоретиков, не имеющих практических навыков. По­этому, несмотря на вывод теоретиков о невозможности «обыграть» ры­нок, любой инвестор всегда надеется на благоприятный для себя исход. Кроме того, оценка по модели (27.1) весьма условна и субъективна, а потому реальная, «истинная» оценка внутренней стоимости любого торгуемого финансового актива неизвестна — этим обусловливается ис­ключительно высокая волатильность цен на финансовом рынке, завися­щая в том числе и от субъективных ожиданий и степени их распростра­нения и влияния на участников рынка.