Вопрос 2. Оптимальное размещение инвестиций

Лекция 7. Формирование портфеля реальных инвестиций

1. Сравнительный анализ проектов разной продолжительности

2. Оптимальное размещение инвестиций

Вопрос 1. Сравнительный анализ проектов разной продолжительности

При формировании портфеля реальных инвестиций может возникнуть ситуация когда i,n Выбор проекта с разной продолжительностью возможет двумя способами.

Расчет суммарного ЧДД повторяющегося потока.

1) Определяется наименьшее общее кратное для числа лет реализации каждого проекта. Например, проект А имеет продолжительность 2 года, а проект Б – 3 года, следовательно, общее кратное этих проектов составит 6 лет. Отсюда можно сделать предположение, что в течение 6 лет проект А может быть повторен трижды (три цикла), а проект Б – два раза (два цикла). Следовательно, проект А будет иметь три годовых платежей: 1-2-й годы, 3-4-й годы и 5-6-й годы, а проект Б два потока: 1-3-й годы и 3-6-й годы.

2) Считая, что каждый из проектов будет повторяться несколько циклов, рассчитать суммарное значение показателя ЧДД для повторяющихся потоков.

3) Выбрать тот проект из исходных, у которого суммарное значение ЧДД повторяющегося потока будет наибольшим.

Суммарный ЧДД повторяющегося потока находится по формуле:

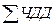i,n = ЧДД_i (1+ + + +.....+ ),

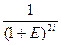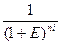где ЧДД_i - чистый дисконтированный доход исходного (повторяющегося потока);

i - продолжительность этого проекта;

n - число повторений (циклов) исходного проекта (число слагаемых в скобках);

Пример:

Имеет ряд инвестиционных проектов, требующих равную величину стартового капитала – 200 тыс. руб. Цена капитала, т.е. предполагаемый доход, составляет 10%. Требуется выбрать наиболее оптимальный из них, если потоки платежей (приток) характеризуется следующими данными, тыс. руб.:

Проект А: 100; 140.

Проект Б: 60; 80; 120.

Наименьшее общее кратное для этих проектов составляет 6 лет. За этот период проект А повторится трижды, проект Б дважды.

0 1 2 3 4 5 6

проект А | ------------|--------------|--------------|-------------|-------------|--------------|

-200 100 140

- 200 100 140

-200 100 140

0 1 2 3 4 5 6

проект Б | ------------|--------------|--------------|-------------|-------------|--------------|

-200 60 80 120

- 200 60 80 120

ЧДД_А = - 200 + -200 + 90,9 + 115,64 = 6,54 тыс.руб.

ЧДД_Б = - 200+ 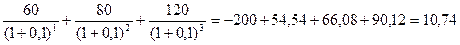тыс.руб.

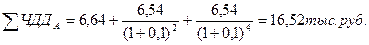
Предпочтение отдается проекту Б, так как у него ЧДД больше.

Метод цепного повтора.

А) Определяется наименьшее общее кратное для числа лет реализации каждого проекта.

Б) Строится шкала, на которой отмечают все повторения проектов

В) Рассчитывается ЧДД проектов.

Г) Выбирается тот проект, у которого ЧДД больше.

Пример:

Имеет ряд инвестиционных проектов, требующих равную величину стартового капитала – 200 тыс. руб. Цена капитала, т.е. предполагаемый доход, составляет 10%. Требуется выбрать наиболее оптимальный из них, если потоки платежей (приток) характеризуется следующими данными, тыс. руб.:

Проект А: 100; 140.

Проект Б: 60; 80; 120.

Наименьшее общее кратное для этих проектов составляет 6 лет. За этот период проект А повторится трижды, проект Б дважды.

0 1 2 3 4 5 6

проект А | ------------|--------------|--------------|-------------|-------------|--------------|

-200 100 140

- 200 100 140

- 60 -200 100 140

- 60

0 1 2 3 4 5 6

проект Б | ------------|--------------|--------------|-------------|-------------|--------------|

-200 60 80 120

- 200 60 80 120

- 80

ЧДД_А = -200 + 100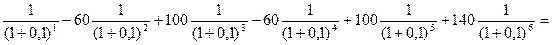

= - 200 + 90,9 – 49,58 + 75,13 – 40,98 + 62,09 + 79,02 = 16,58 тыс. руб.

ЧДД_Б = - 200 =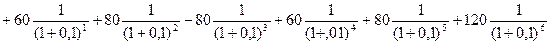

= -200 + 54,54 + 66,11 – 60,1 + 40,98 + 49,67+ 67,73 = 18,99 тыс. руб.

Результаты расчетов одинаковы при использовании того и другого метода.

Вопрос 2. Оптимальное размещение инвестиций

При наличии выбора нескольких привлекательных инвестиционных проектов и отсутствии необходимых денежных ресурсов для участия в каждом возникает задача оптимального размещения инвестиций.

Ниже предлагается к рассмотрению ряд ситуаций, требующих использования методов оптимального размещения.

Пространственная оптимизация.Под пространственной оптимизацией следует понимать решение задача, направленной на получение максимального суммарного прироста капитала, при реализации нескольких независимых инвестиционных проектов, стоимость которых превышает имеющиеся у инвестора финансовые ресурсы. Данная задача предполагает различные методы решения в зависимости от того, возможно или нет дробление рассматриваемых проектов.

Проекты поддаются дроблению.При возможностидробления проектов предполагается реализация ряда из них в полном объеме, а некоторых – только частично. В отношении последних принимается к рассмотрению соответствующая доля инвестиций и денежных поступлений.

Общая сумма, направленная на реализацию проектов не должна превышать лимита денежных ресурсов предназначенных инвестором на эти цели.

Рассматриваемая задача решается в следующей последовательности:

1.Для каждого проекта рассчитывается индекс доходности ИД;

2.Проекты ранжируются по убыванию индекса доходности;

3. К реализации принимаются первые k проектов, стоимость которых в суме не превышает лимита средств предназначенных на инвестиции.

4. При наличии остатка инвестиционных средств они вкладываются в очередной проект, но не в полном объеме, а лишь в той части, в которой может быть профинансирован.

Пример:

Фирма планирует инвестировать в основные фонды 60 млн. руб; цена источников финансирования составляет 10%.

Рассматриваются четыре альтернативных проекта со следующими потоками платежей:

Год 0 1 2 3 4

Проект А -35 11 16 18 17

Проект Б -25 9 13 17 10

Проект В -45 17 20 20 20

Проект Г -20 9 10 11 11

Необходимо составить оптимальный план размещения инвестиций. Рассчитаем ЧДД и ИД для каждого проекта.

Проект А : ЧДД – 13,34; ИД – 1,38

Проект Б: ЧДД – 13,52; ИД - 1,54

Проект В: ЧДД – 1 5,65; ИД – 1,35

Проект Г: ЧДД – 12,215; ИД – 1,61

Проекты, проранжированные по степени убывания показателя ИД, располагаются в следующем порядке: Г, Б, А, В. Исходя из результатов ранжирования, определяем инвестиционную стратегию (таблица 1).

Таблица 1

Проект	Размер инвестиций, млн. руб.	Часть инвестиций включаемая в инвестиционный портфель, %	ЧДД, млн. руб.
Г			12,22
Б			13,52
А	60 – (20 + 25) =15	(15/35) *100=42,86	13,3*0,4286=5,72
Итого			31,46

Проекты не поддаются дроблению.В случае, когда проекты могут быть приняты к реализации только в полном объеме, для нахождения оптимальных вариантов производят просмотр сочетаний проектов с расчетом их суммарного ЧДД. Комбинация, обеспечивающая максимальное значение суммарного ЧДД, считается оптимальной.

Пример:

Используя данные предыдущего примера, составим план оптимального размещения инвестиций, имея в виду, что лимит инвестиций не должен превысить 60 млн. руб., а к реализации могут быть приняты проекты только в полном объеме.

Возможные сочетания проектов и их суммарный ЧДД представим в таблице 2

Таблица 2.

Варианты сочетания проектов	Суммарные инвестиции	Суммарный ЧДД
А+Б	35+25=60	13,34+13,52=26,86
А+В	35+45=80	Сочетание невозможно
А+Г	35+20=55	13,34+12,215=25,555
Б+В	25+45=70	Сочетание невозможно
Б+Г	25+20=45	13,52+12,215=25,735
В+Г	45+20=65	Сочетание невозможно

Сочетание проектов А и Б является оптимальным.

Временная оптимизация инвестиционных проектов. рассматриваются несколько привлекательных проектов однако в результате ограниченности ресурсов они не могут быть реализованы в планируемом году одновременно. Но в следующем году нереализованные проекты либо их части могут быть реализованы. Решение задачи сводится к оптимальному распределению проектов по двум годам.

Последовательность решения:

1. По каждому проекту рассчитывается индекс возможных потерь, характеризующий относительную потерю ЧДД, в случае если проект будет отсрочен к исполнению на год.

Индекс рассчитывается по формуле:

ИП= (ЧДД₁ – ЧДД₀) /К,

где ЧДД₁ – приведенная стоимость рассматриваемого проекта в конце первого года;

ЧДД₀ – дисконтированная величина ЧДД по ставке Е,

т.е.

ЧДД₀ =

где Е - норма дисконта;

К – размер отложенных на год инвестиций.

2. Проекты, обладающие наименьшей величиной индекса возможных потерь, переносятся на следующий год.

Пример. По условиям предыдущего примера составим оптимальный план размещения инвестиций на два года при условии, что инвестиции на планируемый год не могут превысить 75 млн. руб.

Расчет необходимых данных приведен в таблице 3.

Таблица 3

Проект	ЧДД в 1году	Коэффициент дисконтирования по ставке 10%	ЧДД в 0 год (гр.2хгр.3)	Потеря ЧДД (гр.2-гр.4)	Величина отложенной на год инвестиции	Индекс возможных потерь	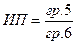Результаты ранжирования по убыванию индекса потерь
А	13,34	0,909	12,13	1,21		0,0346
Б	13,52	0,909	12,29	1,23		0,0492
В	15,62	0,909	14,23	1,42		0,0316
Г	12,22	0,909	11,10	1,12		0,056

Как видно из таблицы 3 наименьшие потери связаны с переносом на следующий год проекта В (ИП =0,0316) и проекта А ( (ИП=0,3446). Следовательно, для реализации в текущем году могут быть приняты проект Б и Г в полном объеме, так как сумма их инвестиций составляет 45 мл. руб., а также часть проекта А. Оставшуюся часть проекта А и проект В целесообразно реализовать в следующем году.

Таблица 4

Проект	Размер инвестиций	Часть инвестиций включаемых в портфель в 0году	ЧДД
Г		100%	12,215
Б		100%	13,52
А		85,7	11,43
Итого			37,16
В 1 году
А		14,3	1,91
В			15,65
Итого			17,55