Стандотклон(ln(а2:а11/а1:а10))* корень(52)}

Лабораторная работа № 9

Моделирование срествами Excel операций с акциями. Модель цены акции.

Цель работы: Освоение практических навыков расчетов по акциям

Волатильность. Цена опциона.

Ранее нами изучались детерминированные денежные потоки. Процентные ставки, выплаты были четко определены. Мы точно вычисляли, какая сумма будет на счете в банке в соответствии с условиями договора. Если непрерывно начисляемая процентная ставка равна m то сумма вклада с течением времени изменяется по закону S_t =S₀e^mt, где S₀— начальное значение вклада.

Эквивалентное утверждение: S_t изменяется в соответствии с дифференциальным уравнением dS_t/dt=mS_t,, которое можно переписать в видеdS_t=mS_t dt. Начальное условие S_t: при t = 0 равняется S₀.

Но имеются активы, цена которых меняется хаотически под действием процессов спроса и предложения. Это акции. Посредством умелой купли-продажи акций можно получить значительную прибыль, существенно превышающую доход от банковского счета или ценных бумаг с фиксированным доходом (облигации). Но и убытки могут оказаться значительными.

Для описания динамики цены акций S_t, П.Самуэльсоном в 1965 г. было предложено использовать так называемое геометрическое броуновское движение

dS_t=mS_t dt+sS_tdw_t

Это дифференциальное уравнение получено из предыдущего добавлением случайного возмущения. Здесь m— коэффициент сноса, w_t— винеровский процесс (весьма упрощенно можно считать, что его производная — "белый шум"), s²— локальная дисперсия. Величину s в финансовой литературе принято называть волатильностью (от английского слова Volatility — из­менчивость). Вычисление этой величины по историческим дан­ным представляет для финансовых аналитиков значительный интерес.

Например, волатильность нужна как параметр в фор­муле Блэка-Шоулса для расчета цены опциона.

Моделирование цены акции. Перепишем модель динамики цены акции для дискретного времени.

S_t – S_t-h= S_t-h (mh+ sеÖh).

Здесь е— нормально распределенная случайная величина с нулевым средним и единичной дисперсией, h — шаг по времени при измерении цены акций.

Но тогда множитель

mh+ sеÖh = f(mh, sеÖh)

— нормально распределенная случайная величина со средним mh и стандартным отклонением sÖh.

Поэтому

S_t = S_t-h (1+f(mh, sеÖh))

Задание 1.

Пусть m= 0.14, s= 0.20. Шаг h = 0.01, т.е. составляет сотую часть года (3,65 дня). Начальная цена акции S₀ =20. Рассчитать 12 шагов для цены акции S_t и безрискового актива В_t с тем же значением m и начальным значением

В₀ =20.

Построить графики S и В на одной координатной плоскости.

Задание 2.

В таблице 1 даны исторические данные— еженедельная цена акций S_t.

St				51,5	50,5		48,5		49,5	50,5

Из этой последовательности надо сформировать новую последовательность 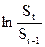, вычислить для нее стандартное отклонение и умножить на используя табличную формулу:

СТАНДОТКЛОН(LN(А2:А11/А1:А10))* КОРЕНЬ(52)}.

Вычисленное значение сообщить преподавателю.

Задание 3. Имеются данные о ежедневной цене закрытия акций (рис. 1). Нечетные строки таблицы — номера дней, четные строки — цена закрытия.

	20 1/8	19 7/8		20 1/2	20 1/4	20 7/8
20 7/8	20 7/8	20 3/4	20 3/4		21 1/8	20 7/8
20 7/8	21 1/4	21 3/8	21 3/8	21 1/4	21 3/4

Рис. 1

Считая, что в году 250 торговых дней, вычислить волатильность.

Результат сообщить преподавателю.