Наращенная величина аннуитета

Получатели поступлений оценивают свой доход суммарной величиной за полный срок действия платежа, разумеется, с учетом временной неравноценности денег.

Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п.

Рис. 8. Логика финансовой операции наращения финансовой ренты

Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 + i).

Рассмотрим определение наращенной суммы на примере наиболее простого случая, – годовой постоянной обычной ренты:

где FVA – наращенная сумма ренты;

R – размер члена ренты, т.е. размер очередного платежа;

i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах,

s _n;i – коэффициент наращения ренты.

Пример. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение:

Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.

Сумма всех взносов с начисленными процентами будет равна:

Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами, содержащими коэффициенты наращения ренты:

FVA = R • s_{5 ; 30} = 500 • 9,0431 = 4'521,55 руб.

Сумма взносов в течение 5 лет составит:

P = n • R = 5 • 500 = 2'500 руб.

Следовательно, сумма начисленных процентов будет равна:

I = FVA - P = 4'521,55 - 2'500 = 2'021,55 руб.

Таким образом, доход владельца счета за 5 лет составит 2'021,55 руб.

Для овладения методами финансовой математики важно не столько запоминание формул, сколько общих принципов расчета.

Для определения наращенной суммы на конец рассматриваемого периода последовательно присоединяются промежуточные результаты наращения к очередному платежу.

Рассмотрим поэтапное решение предыдущего примера:

Расчет наращенной величины аннуитета

Период	Взносы*	Проценты, начисленные за период	Наращенная сумма на конец периода
	500,00	-	500,00
	500,00	150,00	1150,00
	500,00	345,00	1995,00
	500,00	598,50	3093,50
	500,00	928,05	4521,55

* Взносы поступают в конце периода.

Таким образом, получается такая же сумма, как и по формуле наращения аннуитета.

Однако рассматриваемая формула используется только при начислении процентов один раз в год, но возможны случаи и неоднократного начисления процентов в течение года, тогда используют следующую формулу:

где j – номинальная ставка процентов.

Пример. Рассмотрим предыдущую задачу, изменив условия: проценты начисляются поквартально.

Решение:

В этом случае рента с начислением процентов 4 раза в год, а общее количество начислений составит 20 раз. Отсюда сумма всех взносов с начисленными на них процентами будет равна:

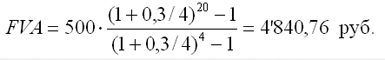Отсюда сумма начисленных процентов будет равна:

I = FVA - P = 4'840,76 - 2'500,00 = 2'340,76 руб.

Как видим, переход от годового начисления процентов к ежеквартальному начислению заметно увеличил как наращенную сумму, так и сумму процентов.

Бывают случаи, когда рентные платежи вносятся несколько раз в год равными суммами (срочная рента), а начисление процентов производится только раз в году. Тогда наращенная величина ренты будет определяться по формуле:

Также нередки случаи, когда рентные платежи вносятся несколько раз в году и начисление процентов также происходит несколько раз в год, но число рентных платежей не равно числу периодов начисления процентов, т.е. p ≠ m. Тогда формула по которой можно определить наращенную величину финансовой ренты примет вид:

На практике большее распространение получил поток постнумерандо, поскольку согласно общим принципам учета принято подводить итоги и оценивать финансовый результат операции или иного действия по окончании очередного отчетного периода. Что же касается поступления денежных средств в счет оплаты, то на практике они чаще всего распределены во времени неравномерно и поэтому для удобства все поступления относят к концу периода, что позволяет использовать формализованные алгоритмы оценки.

Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз.

Для годовой ренты пренумерандо с начислением процентом один раз в год формула примет вид:

Для годовой ренты пренумерандо с начислением процентов несколько раз в год: