Формулы современной величины
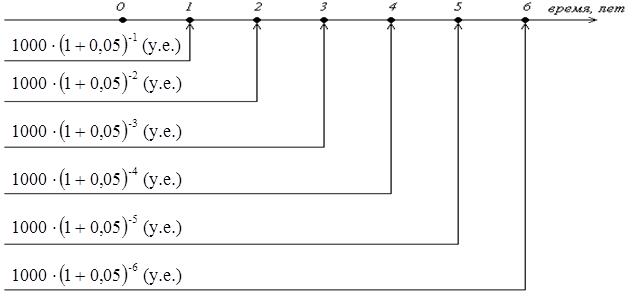
Пример 3.4. Какую сумму нужно внести в банк, выплачивающий 5% годовых, чтобы иметь возможность в течении последующих 6 лет ежегодно получать по 1000 у.е. (Предполагается, что после последней выплаты на счете нечего не останется).
 Решение:
Решение:
Чтобы через 1 год получить 1000 у.е., надо в начале вложить 1000∙ (1+0,05)-1 у.е.
Чтобы через 2 года получить 1000 у.е., надо в начале вложить
1000∙ (1+0,05)-2 у.е.
…
Чтобы через 6 лет получить 1000 у.е., надо в начале вложить
1000∙ (1+0,05)-6 у.е.
Таким образом, чтобы в течение 6 лет получать по 1000 у.е., надо в начале вложить следующую сумму:
A = 1000∙ (1+0,05)-1 + 1000∙ (1+0,05)-2 + 1000∙ (1+0,05)-3 + 1000∙
∙ (1+0,05)-4 + +1000∙ (1+0,05)-5 + 1000∙ (1+0,05)-6 ;
A = 1000∙ (1,05-1 + 1,05-2 +1,05-3 +1,05-4 +1,05-5 +1,05-6) = 5075,69 (у.е.)
В общем виде формула имеет вид:
A = R∙ [(1+i)-1 + (1+i)-2 +…+ (1+i)-n]
В квадратных скобках сумма членов геометрической прогрессии:
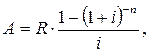 | (3.7) |
где
R – годовой платеж;
i – процентная ставка.
Если платежи производят « р » раз в году, а начисление процентов « j » производят « m » раз в году, то формула имеет вид:
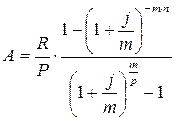 |
| (3.8) |
Если m = p, количество платежей равно количеству периодов начисления процентов.
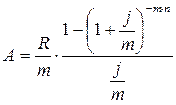 | (3.9) |
Пример 3.4. Взят кредит 120000 рублей для приобретения жилья. Срок погашения кредита – 2 года. Процентная ставка – 25% годовых при ежемесячном начислении процентов. Каковы должны быть ежемесячные платежи, если по условию кредитного соглашения они должны быть одинаковыми?
| Дано: | Решение: |
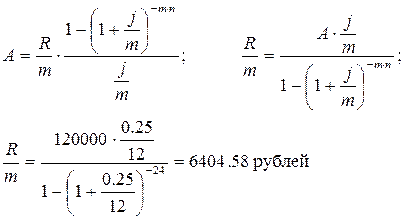 A = 120000 руб. m = p = 12 j = 0,25 = 25% n = 2 года A = 120000 руб. m = p = 12 j = 0,25 = 25% n = 2 года | |
| R/m = ? | Ответ: 6404,58 рублей. |
Другими словами, получив кредит на 2 года под 25% годовых при ежемесячном начислении процентов, заемщику придется в течении 2 лет каждый месяц платить 6404,58 рублей.
Всего за 2 года будет заплачено 6404,58∙ 24 = 153709,98 рублей.
План погашения кредита.
Одним из пунктов кредитного соглашения, как правило, является план погашения кредита. Рассмотрим план погашения кредита на примере:
Пример 3.5. Кредит 100000 рублей взят на 4 года под 20% годовых, начисляемых на непогашенный остаток по схеме сложных процентов. Возвращать надо равными суммами в конце каждого года. Составить план погашения кредита.
| Дано: | Решение: |
| A = 100000 руб. j = 0,20 = 20% n = 4 года | |
| R = ? | Ответ: 38628,91 рублей. |
Таблица 1. План погашения кредита.
| № | Сумма долга на начало периода руб. | Сумма процентных денег за период, руб. | Погасительный платеж руб. | Сумма погашенного долга, руб. |
| 38628,91 | 18628,91 | |||
| 81371,09 | 16274,22 | 38628,91 | 22354,69 | |
| 59016,40 | 11803,28 | 38628,91 | 26825,63 | |
| 32190,77 | 6438,14 | 38628,91 | 32190,77 | |
| Итого | 54515,64 | 154515,64 | 100000,00 |
1) Заполняем столбец 4:
В каждой строке этого столбца записываем 38628,91. Это означает, что каждый год за кредит придется платить по 38628,91 рублей.
2) В 1ой строке столбца 2 записываем сумму долга – 100000 рублей.
3) В 1ой строке столбца 3 записываем сумму процентных денег - 100000∙0,20 = 20000 рублей.
4) В 1ой строке столбца 5 записываем сумму погашаемого долга за 1й год – 38628 – 20000 = 18628,91 рублей.
5) Во 2й строке столбца 2 записываем сумму долга на начало 2го года – 100000 – 18628,91 = 81671,09 рублей.
6) Во 2й строке столбца 3 записываем сумму процентных денег за 2ой год – 81371,09∙0,20 = 16274,22 рублей.
7) Во 2й строке столбца 5 записываем сумму погашения долга за 2ой год – 81371,09∙0,20 = 16274,22 рубля.
Далее все аналогично рассчитывается для 3го и 4го годов и заполняется вся таблица 1. Причем сумма всех значений: в столбце 5 (сумма погашенного долга) должна быть равна сумме кредита; в столбце 3 – сумма всех выплаченных процентных денег; в столбце 4 (все заплаченные за кредит деньги) равна сумме итоговых значений в столбце 3 и столбце 5.
Рассмотрим тот же самый пример для случая, когда проценты начисляются несколько раз в году.
Пример 3.6. Кредит 100000 рублей взят на 4 года под 20% годовых, начисляемых на непогашенный остаток ежемесячно. Возвращать надо равными суммами в конце каждого года. Составить план погашения кредита.
| Дано: | Решение: |
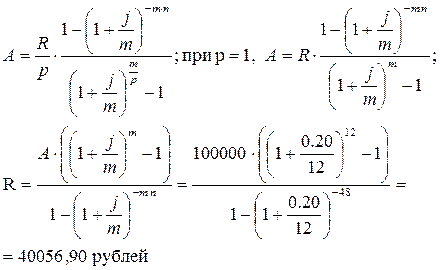 A = 100000 руб. j = 0,20 = 20% n = 4 года m = 12 p = 1 A = 100000 руб. j = 0,20 = 20% n = 4 года m = 12 p = 1 | |
| R = ? | Ответ: 40056,90 рублей. |
Таблица 2. План погашения кредита.
| № | Сумма долга на начало периода, Руб. | Сумма процентных денег за период, руб. | Погасительный платеж, руб. | Сумма погашенного долга, руб. |
| 21939,11 | 40056,90 | 18117,79 | ||
| 81882,21 | 17964,23 | 40056,90 | 22092,67 | |
| 59789,54 | 13117,29 | 40056,90 | 26939,61 | |
| 32849,93 | 7206,97 | 40056,90 | 32849,93 | |
| Итого | 60227,60 | 160227,60 | 100000,00 |
1) Заполняем столбец 4.
В каждой строке этого столбца записываем 40056,90 рублей. Это означает , что каждый год за кредит придется платить по 40056,90 рублей.
2) В 1ой строке столбца 2 записываем сумму долга – 100000 рублей.
3) В 1ой строке столбца 3 записываем сумму процентных денег –
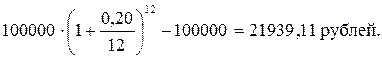 |
4) В 1ой строке столбца 5 записываем сумму погашенного долга за 1й год – 40056,90 – 21939,11 = 18117,79 рублей.
5) Во 2ой строке столбца 2 записываем сумму долга на начало 2го года – 100000 – 18117,79 = 81882,21 рублей.
6) Во 2ой строке столбца 3 записываем сумму процентных денег за
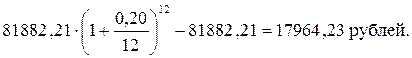 |
2ой год –
7) Во 2ой строке столбца 5 записываем сумму погашенного долга за 2ой год – 40056,90 – 17964,23 = 22092,67 рублей.
Далее все аналогично рассчитывается для 3го и 4го годов и заполняется вся таблица 2.
Итого заплачено за кредит 160227,60 рублей из них 100000,00 рублей – основной долг и 60227,60 рублей – процентные деньги.
Инфляция
Понятие инфляции.
Инфляция – это процесс обесценивания национальной валюты, т.е. снижения ее покупательной способности и общего повышения цен в стране.
Инфляция по-разному влияет на участников кредитного соглашения. Кредитор может потерять часть своего дохода из-за обесценивания денежных средств. Заемщик наоборот выигрывает, т.к. может погасить задолжность денежными средствами сниженной покупательной способности.
Рассмотрим процесс влияния инфляции на результат финансовых операций.
Один из параметров, характеризующих инфляцию, – это уровень инфляции за год α. Он показывает на сколько процентов за год из-за инфляции вырастут цены.
Если L – первоначальная цена товара, то
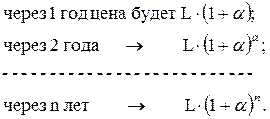 |
(1+ α)n = Ia – индекс инфляции. Он показывает, во сколько раз выросли цены на товары из-за инфляции за рассматриваемый период.
Отметим, что индекс инфляции вычисляется по формулам, похожим на формулы сложных процентов. Если рассматриваемый период не является целым числом, т.е. n=n0+l, где n0 – целое число лет, а l – дробное, то:
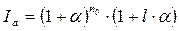 |
Пример 4.1. Уровень инфляции 23%. Найти индекс инфляции за 7 месяцев.
| Дано: | Решение: |
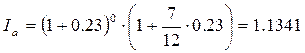 n0 = 0 l = 7/12 α = 23% = 0,23 n0 = 0 l = 7/12 α = 23% = 0,23 | |
| Ia = ? | Ответ: это означает, что в среднем цены за 7 месяцев вырастут на 13,41%. |
