Построение и анализ регрессионной модели

Выполним построение уравнения множественной линейной регрессии, где в качестве эндогенной переменной примем объем краткосрочных кредитов, а в качестве независимых

X1 – уровень номинальной заработной платы

X2 – ставка рефинансирования.

Множественная регрессия имеет вид:

У=225,72 + 0,263 х₁ - 9,085 х₂.

Значение параметров a, b₁, b₂ с учетом округления:

225,72; 0,263; -9,085.

Значимость уравнения множественной регрессии в целом оценивается с помощью с помощью F-критерия Фишера:

,

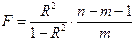где 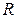- индекс множественной корреляции;

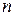- число наблюдений;

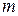- число факторов.

Полученное по формуле значение F сравнивается с табличным при уровне значимости 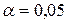. Если фактическое значение F-критерия Фишера превышает табличное, то уравнение статистически значимо с вероятностью 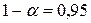. При использовании таблицы следует принимать 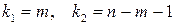. F_кр(0,05; 2; 45)=3,23.

По данным таблицы Fфакт=173,84 вероятность получить такой результат равен 6,78E-10, что не превышает допустимый уровень значимости 5%.

Значения скорректированного и некорректированного линейных коэффициентов множественной детерминации приведены в рамках регрессионной статистики. Некорректированный коэф-т множественной детерминации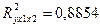

Оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата.

Здесь эта доля составляет 88% и указывает на тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации 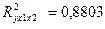определяет тесноту связи с учетом степени свободы общей и остаточной дисперсии.

Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели.

Оценим статистическую значимость коэффициентов регрессии можно с помощью t-статистики:

t_b0 = 4,32; t_b1 = 17,299, t_b2 = -3,85.

Найдем критическую точку распределения Стьюдента. В нашем случае .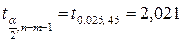

Сравниваем значения t-статистик со значением критической точки Стьюдента:

4,32 > 2,021, значит условие статистической значимости выполняется для параметра b₀;

17,299 > 2,021, значит коэффициент b₁ статистически значим, а значит переменная X₁ имеет существенное линейное влияние на Y;

|-3,85| > 2,021, значит коэффициент b₂ статистически значим, а значит переменная X₂ имеет существенное линейное влияние на Y.

Таким образом, качество построенной линейной модели весьма высокое – все входящие переменные являются статистически значимыми, коэффициент детерминации превышает 88%. Знаки при коэффициентах соответствуют теоретически обоснованным.

Однако в разделе корреляционный анализ было показано, что квадратичная запись обеих переменных дает лучший результат. Построим уравнение с включение дополнительно X₁² и X₂².

Множественная регрессия имеет вид:

У=479,86 - 0,019 х₁ - 5,168 х₂ + 0,00004 х₁² + 0,056 х₂².

Значимость уравнения множественной регрессии в целом оценивается с помощью с помощью F-критерия Фишера:

,

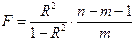где 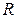- индекс множественной корреляции;

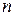- число наблюдений;

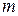- число факторов.

Полученное по формуле значение F сравнивается с табличным при уровне значимости 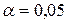. Если фактическое значение F-критерия Фишера превышает табличное, то уравнение статистически значимо с вероятностью 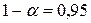. При использовании таблицы следует принимать 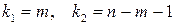. F_кр(0,05; 4; 45)= 2,61.

По данным таблицы Fфакт = 92,57 вероятность получить такой результат равен 1,5-20, что не превышает допустимый уровень значимости 5%.

Значения скорректированного и некорректированного линейных коэффициентов множественной детерминации приведены в рамках регрессионной статистики. Некорректированный коэф-т множественной детерминации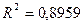

Оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата.

Здесь эта доля составляет 89% и указывает на тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации 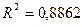определяет тесноту связи с учетом степени свободы общей и остаточной дисперсии.

Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели.

Оценим статистическую значимость коэффициентов регрессии можно с помощью t-статистики:

t_b0 = 3,033; t_b1 = -0,122, t_b2 = -0,283, t_b3 = 1,906, t_b4 = 1,187.

Найдем критическую точку распределения Стьюдента. В нашем случае .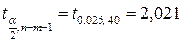

Сравниваем значения t-статистик со значением критической точки Стьюдента:

Условие статистической значимости не выполняется ни для одного параметра, значит все переменные являются статистически незначимыми. Построение данного уравнения не оправдано.