Наращение простыми процентами
Известны две основные схемы дискретного начисления, т.е. начисления процентов за фиксированные в договоре интервалы времени:
- схема простых процентов;
- схема сложных процентов.
Схема простых процентов предполагает неизменность величины, с которой происходит начисление. Пусть исходный инвестируемый капитал равен P; требуемая доходность – r. Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину P*r. Таким образом, размер F инвестированного капитала через n лет будет равен:

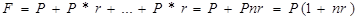 (3.1)
(3.1)
Выражение (2.1) называется формулой наращения по простым процентам или формулой наращения простыми процентами, а множитель (1+nr) – множителем наращения или коэффициентом наращения простых процентов. Величина дохода или величина процента:
I = Pnr (3.2)
Пример
Найти величину процента и наращенную сумму за трёхлетний кредит в 20 тыс. руб., взятый под 9%.
Здесь P=20 тыс. руб., n=3 года, r=0,09. Тогда
I=20*3*0,09=5,4 тыс. руб.
F=P+I=20+5,4=25,4 тыс. руб. или
F=20*(1+3*0,09)=25,4 тыс. руб.
Необходимо отметить, что размерности n и r всегда должны быть согласованы. Таким образом, либо n должно измеряться в годах, либо с изменением размерности n (например, не годы, а кварталы) ставка процента должна отражать рост за новую единицу времени (за квартал).
С этих позиций наращение по простым процентам в случае, когда продолжительность n финансовой операции не равна целому числу лет, определяется по формуле:
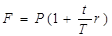 (3.3),
(3.3),
где t – продолжительность финансовой операции в днях;
T – количество дней в году.
Тогда t’=t/T – продолжительность финансовой операции, уже измеряемая в годах (т.е. в данной ситуации n=t’=t/T).
Пример
Клиент поместил в банк вклад в сумме 3,5 тыс. руб. под 24% годовых с ежемесячной выплатой процентов. Какую сумму клиент будет получать каждый месяц?
Так как в этих условиях P=3,5 тыс. руб., n=1/12 года, r=0,24, то по формуле (3.2.2) I=3,5*1/12*0,24=0,07 тыс. руб.
На рисунке 3.2 графически показано наращение по простым процентам.
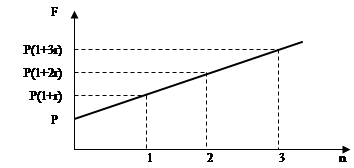 |
Рисунок 2.3.1 - Наращение по простым процентам
Наращение по простым процентам применяется в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору. Простые проценты применяют и при выдаче широко распространённых краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократным начислением процентов.
Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день. Существует три методики исчисления продолжительности финансовой операции:
- немецкая: 360/360;
- французская: 365/360;
- английская: 365/365.
Пример
Предоставлена ссуда в размере 7 тыс. руб. 10 февраля с погашением 10 июня под 20% годовых (год невисокосный). Рассчитать различными способами сумму к погашению (F).
Величина уплачиваемых за пользование ссудой процентов зависит от числа дней, которое берётся в расчёт. Точное число дней составляет: 18 дней февраля + 31 день марта + 30 дней апреля + 31 день мая + 10 дней июня = 120 дней. Приближённое число дней равно: 18 дней февраля + 90 дней (по 30 дней трёх месяцев: март, апрель, май) + 10 дней июня = 118 дней.
Возможные варианты возврата долга:
1. английская методика: F=7(1+120/365*0,2)=7,460 тыс. руб.
2. французская методика: F=7(1+120/360*0,2)=7,467 тыс. руб.
3. немецкая методика: F=7(1+118/360*0,2)=7,459 тыс. руб.
