Способы расчета процентной ставки по ипотечному кредиту

Методические основы расчета ставки процента по ипотечным кредитам.

Банковский ипотечный кредит, как и любой другой кредитный договор всегда возмезден.

Согласно п.1. ст. 819 ГК РФ по кредитному договору банк или иная кредитная организация (кредитор) обязуются предоставить денежные средства (кредит) заемщику в размере и на условиях, предусмотренных договором, а заемщикобязуется возвратить полученную денежную сумму и уплатить проценты на нее.

По мнению специалистов, различается несколько групп однородных ставок, характерных для отдельных секторов рынка ссудных капиталов: официальная учетная ставка, ставки рынка ценных бумаг, ставки по операциям банков и других кредитных институтов с небанковскими заемщиками и кредиторами.

Процентные ставки подразделяются также:

1) на долгосрочные и краткосрочные;

2) на основные и второстепенные (меняются вслед за основными);

3) на рыночные (величина и колебания которых зависят от экономической конъюнктуры) и регулируемые (центральным банком, банковским консорциумом, другими кредитными институтами);

Помимо них существуют ставки, применяемые исключительно на национальных кредитных рынках, в отличие от ставок, используемых одновременно в сфере внутреннего и международного кредита (их уровень зависит от изменения валютных курсов и других факторов).

Сложные проценты Для начала необходимо вспомнить про инфляцию, ведь и она является причиной переплаты по процентной ставке.

Общая формула для вычисления:

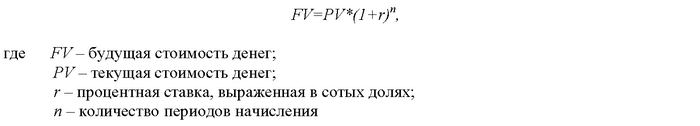
По этому в сумму процентов, декларированных к уплате ипотечного процента, входит, помимо банковских наценок, еще и инфляционные изменения ценности денег.

Но инфляция – не единственная причина существования процентов. Ведь даже в условиях стабильной экономики при отсутствии инфляции займодавцы хотят что-то получить с заемщиков, кроме суммы долга.

Простые проценты

Главное правило – проценты начисляются только на основную сумму долга (а в «сложной» формуле – еще и проценты на проценты). Математически эта операция проще, хотя экономически менее справедлива.

Общая формула:

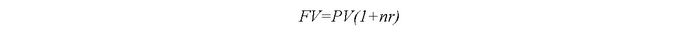
Способы расчета процентной ставки по ипотечному кредиту

Самый простой путь – равномерное погашение кредита с уплатой процентов на остаток задолженности – аналогичен регулярному снятию процентов с банковского вклада. Тут разницы между простыми и сложными процентами нет

В общем виде получаются следующие формулы:

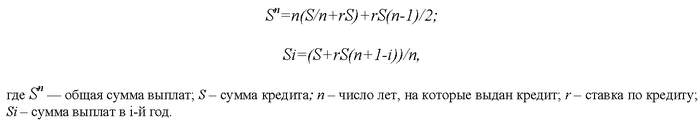
(Для удобства считаем, что проценты платятся ежегодно, хотя чаще встречаются ежемесячные выплаты. Формула станет более громоздкой, но принципиальных отличий не будет.)

Банку этот вариант выгоден: он быстрее получает деньги назад, но вот заемщику обычно хочется сдвинуть выплаты подальше в будущее и платить равными долями (а лучше – с постепенным увеличением выплат).

А по второму варианту мы платим проценты на всю сумму кредита в течение всего срока! В том числе и на ту часть, которую давно вернули!

Общая формула:

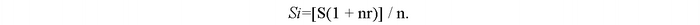
Это просто ростовщический подход, и в чистом виде он встречается редко, по крайней мере, у солидных банков.

Чтобы понять, какие суммы выплачиваются при равных регулярных платежах, вернемся к понятию дисконтирования, ведь выплаты разделены временем, и просто складывать их – не вполне корректно. Правильнее найти их суммарную приведенную стоимость, а потом в формулу подставить сумму кредита и определить, чему равен разовый платеж. Исходный момент – выдача кредита в «нулевом году».

Пусть выплаты составляют А рублей в год на протяжении n лет при годовой процентной ставке r. Дисконтированная выплата рублей в конце первого года равна А/(1+r). Дисконтированная выплата второго года составит А/(1+r)² и т. д. Получается геометрическая прогрессия с первым членом А/(1+r) и знаменателем 1/(1+r). Первоначальная сумма кредита (дисконтированная) составит:

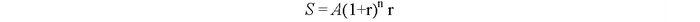
Разделив величину кредита (в нашем случае 20 000 долл.) на выражение (1+r)ⁿ r (аннуитетный множитель), получим искомую сумму разового платежа.

Аннуитетный множитель зависит от процентной ставки и числа периодов; его можно найти в специальных таблицах.

В этой сумме уже есть и проценты, и постепенное погашение основного кредита. Год от года доля процентов снижается.

Если третья схема типична для западного банка, то первая – для банка российского, озабоченного собственной судьбой больше, чем благом заемщика. Ведь к моменту погашения кредита может не только измениться экономическая ситуация в России, но и исчезнуть сама рыночная экономика. И банк хочет вернуть свои деньги как можно скорее.

Но заемщику это не очень-то удобно. И некоторые банки устанавливают определенную сумму регулярных отчислений в счет погашения кредита, а на оставшуюся сумму начисляют проценты. При такой схеме образуется некоторый «хвост», погашаемый в конце срока. Например, при сумме кредита в те же 20000 долл. заемщик погашает в течение 9 лет по 1500 долл. (плюс проценты на остаток), а в десятый год платит последние 6500 долл. (плюс годовые проценты по ним). Общая формула:

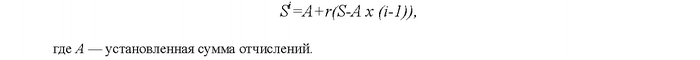
В этом случае общая сумма выплат будет большей, чем в первой и третьей схемах (при той же приведенной стоимости). Но взамен банк принимает на себя дополнительные риски, связанные как с невозвратом, так и с возможным ростом инфляции: «хвост», погашение которого отложено, обесценится сильнее, чем это было бы при равномерных выплатах.