Оценка приведенного денежного потока

Годы						Итого
1) Денежный поток (сумма возврата долга), тыс. грн.
2) Дисконтирующий множитель FM2(r, i) при r = 15 % (данные табличного табулирования)	0,870	0,756	0,658	0,572	0,497
3) Приведенный поток (сумма в долг с позиции текущего момента) стр.1 x стр. 2, тыс. грн.	17,40	18,90	9,87	20,02	19,88	86,07

Денежный поток с равными поступлениями в течение ограниченного промежутка времени называется срочным аннуитетом. В этом случае пос-тупления денежных потоков делаются в конце равных временных интервалов, на которые разбит данный промежуток времени (к примеру, регулярно поступающие рентные платежи за пользование сданными в аренду земельным участком).

Тогда

Р₁ = Р₂ = …= Р_n = А,

где А – величина аннуитета.

К примеру, если бы была возможность ежегодного получения аннуитета и дальнейшего его инвестирования на условиях банковского процента (или других условиях), то к концу четырёхлетнего периода накопленная сумма может быть рассчитана по схеме:

к концу первого периода будет получен аннуитет А;

к концу второго года будет получен новый аннуитет А и приращение к нему в результате вложения полученной суммы аннуитета за первый период в банк под банковский процент, который составит процентную ставку r, т. е. А·(1+ r);

к концу третьего года будет получен новый аннуитет и приращение к нему по результатам вложения суммы аннуитета с приращением конца второго

периода в банк, т. е. А·(1+ r)·(1+ r) = (1+ r)² ;

к концу четвёртого года будет получен новый аннуитет и приращение к нему по результатам вложения суммы аннуитета с приращениями конца третьего периода в банк, т. е. А·(1+ r)²·(1+ r) = (1+ r)³ .

Соответственно, в n-ный период времени сумма аннуитета с приращениями составит:

А·(1+ r)^{n - 1}.

Денежный поток примет вид:

А; А·(1+ r); А·(1+ r)²; А·(1+ r)³; А·(1+ r) ^n-1.

В другом виде формула денежного потока примет вид:

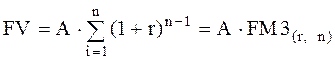, [8.14]

где 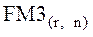– факторный множитель, смысл которого заключается в том, что он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например одна гривна) к концу срока его действия.

Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета.

Значения факторного множителя 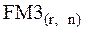табулированы в специальных таблицах.

К примеру, предпринимателю предложено инвестировать 100 тыс. грн. на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 тыс. грн.); по истечении пяти лет выплачивается дополнительное вознаграждение в размере 80 тыс. грн. Следует ли такое предложение принять, если у него есть «безопасная» возможность положить деньги на счёт в банке из расчёта 15 % годовых.

Для принятия решения нужно сравнить две суммы: возвращённую из банка к концу пятилетнего периода и альтернативную сумму доходов от принятого предложения.

К концу пятилетнего периода возвращённая сумма из банка составит:

Р₅ = Р·(1+ r)⁵ = 100·(1+ 0,15)⁵ = 262,35 тыс. грн.

К концу пятилетнего периода альтернативная сумма доходов по результатам принятого предложения составит:

а) дополнительные вознаграждения – 80 тыс. грн.;

б) денежный поток при заданных величинах регулярного поступления (А) в сумме 20 тыс. грн. и процентной ставке r = 15% составит ( 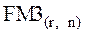= 6,742 – из таблиц табулирования):

Р₅ = А·FM4_{(r, n)} = 20·6,742 = 134,84 тыс. грн.;

в) общая сумма возврата составит

Р₅ = 80 + 134,84 = 214,84 тыс. грн.

Таким образом, предложение нельзя считать целесообразным.

При решении обратной задачи срочного аннуитета (оценка будущих денежных поступлений с позиции текущего момента или текущей стоимости срочного аннуитета) используют (рассуждения такие же, как и при получении формулы 8.14, но при обратном денежном потоке или его дисконтировании) формулу:

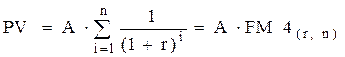. [8.15]

Экономический смысл дисконтирующего множителя 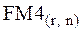заключается в том, что он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например гривни), продолжающегося n лет с заданной процентной ставкой r. Значения этого множителя также табулированы в специальных таблицах.

Бессрочный аннуитет – это денежный поток с равными поступлениями, продолжающийся достаточно длительное время (в практике инвестиционного анализа к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет).

Прямая задача в этом случае не имеет смысла. Что касается обратной задачи, то её решение возможно по формуле:

.

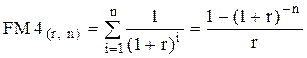Тогда:

,

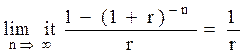откуда

,

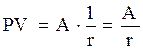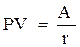. [8.16]

Такая формула чаще всего используется для оценки целесообразности приобретения аннуитета. В этом случае известен размер годовых поступлений, а в качестве коэффициента дисконтирования r обычно принимается гарантированная процентная ставка (к примеру процент, предлагаемый государственным банком).

Определим текущую стоимость бессрочного аннуитета с ежегодным поступлением 600 тыс. грн., если банковский процент государственного банка составляет 11 %.

Тогда:

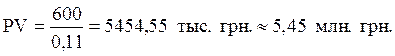
Можно сделать вывод, что если аннуитет предлагается по цене, не превышающей 5,45 млн. грн., он представляет собой выгодную инвестицию, обеспечивающую больший денежный поток, чем поток средств от вложения денег в государственный банк.