Типовые задачи с решениями
Кафедра экономики
Финансовая математика
Методические указания к практическим занятиям
и самостоятельной работе
для студентов направлений
230100.62 Информатика и вычислительная техника
230200.62 Информационные системы
Томск 2012
Содержание
Занятие № 1. Простые ссудные ставки.. 3
Занятие 2. Простые учетные ставки.. 7
Занятие 3. Сложные ссудные ставки.. 11
Занятие 4. Сложные учетные ставки.. 15
Занятие 5. Эквивалентные и эффективные ставки.. 19
Занятие 6. Замена и консолидация платежей.. 23
Задачи для подготовки к занятию... 28
Задание на практическое занятие 6. Замена и консолидация платежей. 28
Занятие 7. Начисление процентов в условиях инфляции.. 30
Занятие 8. Налоги и начисление процентов. 35
Занятие 9. Финансовые ренты.. 39
Занятие 10. Определение параметров ренты.. 43
Занятие 11. Конверсия и замена рент. 47
Занятие 12. Практическое приложение финансовых вычислений.. 52
Методические указания по самостоятельной работе. 57
Занятие № 1. Простые ссудные ставки
Денежные ресурсы, участвующиев финансовой операции, имеют временную ценность, смысл которой может быть выражен следующим утверждением: одна денежная единица, имеющаяся в распоряжении инвестора в данный момент времени, более предпочтительна, чем та же самая денежная единица, но ожидаемая к получению в некотором будущем. Эффективность любой финансовой операции, предполагающей наращение исходной суммы P до ожидаемой в будущем к получению суммы F (F>P), может быть охарактеризована ставкой.
Простая ссудная ставка рассчитывается отношением наращения (F-P) к исходной (базовой) величине P.
Схемапростых процентов предполагает неизменность базы,с которойпроисходит начисление.
В финансовых вычислениях базовым периодом являетсягод,поэтому обычно говорят о годовой ставке. Вместе с тем достаточно широко распространены краткосрочные операции продолжительностью до года. В этом случае за основу берется дневная ставка, причем в зависимости от алгоритмов расчета дневной ставки и продолжительности финансовой операции результаты наращения будут различными. Используются три варианта расчета: а) точный процент и точное число дней финансовой операции – обозначение 365/365 ; б) обыкновенный процент и точное число дней финансовой операции -обозначение 365/360; в) обыкновенный процент и приблизительное число дней финансовой операции- обозначение 360/360.
Математическое дисконтирование является процессом, обратным к наращению первоначального капитала. При математическом дисконтировании решается задача нахождения такой величины капитала (так называемой «приведенной стоимости»), которая через заданное время при наращении по данной процентной ставке будет равна сумме, ожидаемой к получению (уплате) через заданное время.
Возможно финансовое соглашение, предусматривающее изменение во времени ссудной ставки.
Любая финансовая операция предусматривает участие, как минимум, двух сторон: кредитора (инвестора) и заемщика (получателя финансовых ресурсов); это обстоятельство является существенным для вынесения суждения об эффективности некоторой операции. Так, экономическая интерпретация ставки вообще и ее значения в частности зависит от того, с чьих позиций - кредитора или заемщика она дается. Для кредитора ставка характеризует его относительный доход; для заемщика - его относительные расходы. Поэтому кредитор всегда заинтересован в высокой ставке или в повышении ставки; интересы заемщика - прямо противоположны.
Цель проведения занятия- научиться проводить расчеты по схеме простых ссудных процентов, используя формулы финансовых вычислений.
Основные формулы
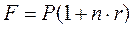 (1.1)
(1.1)
 (1.2)
(1.2)
F=P∙(1+r×t /T) (1.3)
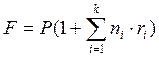 (1.4)
(1.4)
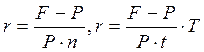 (1.5)
(1.5)
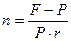 (1.6)
(1.6)
где
P - вложенная сумма;
F – наращенная сумма;
n - количество периодов продолжительности финансовой операции;
r- простая ссудная ставка;
Типовые задачи с решениями
Задача 1.Вы поместили в банк вклад 100 тыс. руб. под простую процентную ставку 6% годовых. Какая сумма будет на счете через 3 года? Какова величина начисленных процентов?
Решение
По формуле (1.1.) при Р=100 тыс. руб., n=3, r =0,06 получаем :
F=100 ×(1+3×0,06)=118 тыс. руб.
Через три года на счете накопится 118 тыс. рублей.
Величина начисленных за три года процентов составит:
118 -100=18 тыс. руб.
Задача 2.На какой срок необходимо поместить денежную сумму под простую процентную ставку 8% годовых, чтобы она увеличилась в 2 раза?
Решение
Искомый срок определяем из равенства множителя наращения величине 2 :
1+n×0,08=2, поэтому
n=1/0,08=12,5 лет.
Сумма, размещенная в банке под 8% годовых, в два раза увеличится через 12,5 лет.
Задача 3.Ссуда в сумме 3000 долл. предоставлена 16 января с погашением через 9 месяцев под 25 % годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов : а) обыкновенный процент с точным числом дней; б) обыкновенный процент с приближенным числом дней; в) точный процент с точным числом дней .
Решение
а) По формуле (1.3), используя обыкновенный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим:
F=3000∙(1+0,25×273/360=3568,75 долл.
Сумма к погашению равна 3568,75 долл.
б) По формуле (1.3), используя обыкновенный процент с приближенным числом дней, рассчитанным по финансовым таблицам (t=9×30=270 дня),получим:
F=3000∙ (1+0,25×270/360)=3562,5 долл.
Сумма к погашению равна 3562,5 долл.
в) По формуле (1.3), используя точный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим:
F=3000∙ (1+0,25×273/365)=3560,96 долл.
Сумма к погашению равна 3560,96 долл.
Задача 4.В финансовом договоре клиента с банком предусмотрено погашение долга в размере 8,9 тыс. руб. через 120 дней при взятом кредите в размере 8 тыс. руб. Определить доходность такой сделки для банка в виде годовой процентной ставки при использовании банком простых обыкновенных процентов.
Решение
По формуле (1.5) при F=8,9 тыс. руб., P= 8 тыс. руб., t= 120 дней, T=360 дней, получим :
r=360×(8,9-8)/ (8×120)= 0,3375=33,75%.
Доходность банка составит 33,75 процентов годовых.
Задача 5.Господин Х поместил 160 тыс. руб. в банк на следующих условиях: в первые полгода процентная ставка равна 8% годовых, каждый следующий квартал ставка повышается на 1%. Какая сумма будет на счете через полтора года, если проценты начисляются на первоначальную сумму вклада? Какую постоянную ставку должен использовать банк, чтобы сумма по вкладу не изменилась?
Решение
Применяя формулу (1.4), получим :
F=160×(1+0,5×0,08+0,25×0,09×+0,25×0,1+0,25×0,11+0,25×0,12)= 183,2
Через полтора года на счете накопится 183 200 руб.
Постоянную ставку, которую должен использовать банк, для того чтобы сумма, накопленная на счете, не изменилась, находим из уравнения:

r=0,096667=,9,67%
Постоянная ставка, которую должен использовать банк, для того чтобы сумма, накопленная на счете, не изменилась, равна 9,67 % годовых.
Задача 6.Кредит выдается под простую ссудную ставку 24 % годовых на 250 дней. Рассчитать сумму, полученную заемщиком, и сумму процентных денег, если необходимо возвратить 3500 тыс. руб.
Решение.
По формуле (1.2) при F = 3500; n=250/365; r=0,24 получаем:
P = 3500 /(1 + 0,24 ·250/365) =3017, 2
Сумма, получаемая заемщиком, составит 3 017 200 руб.
Сумма процентных денег равна (3 500 000 - 3 017 200) = 482 800 тыс. руб.
