Тема 5. Статистическое изучение взаимосвязей и взаимозависимостей между явлениями и их признаками

Методические указания

В процессе изучения темы необходимо усвоить классификацию связей по различным признакам, систему методов и показателей, направленных на их выявление и измерение, на необходимые предпосылки для их применений. Обратите внимание на метод аналитических группировок, без которого не обходится изучение взаимосвязей. Применение метода группировок в изучении связей специфично в случаях, когда это касается взаимосвязи количественных и качественных признаков.

Задача 1. Определите тесноту связи с помощью коэффициента Фехнера между среднегодовой стоимостью основных производственных фондов и долей ручных работ по 12 однотипным предприятиям:

№ предприятия	Среднегодовая стоимость основных производственных фондов, млн. руб.	Доля ручных работ, в %	№ предприятия	Среднегодовая стоимость основных производственных фондов, млн. руб.	Доля ручных работ, в %
	20,6 8,9 32,7 10,2 28,4 12,4	18,6 36,5 40,4 18,9 22,7 28,6		26,4 11,7 50,9 44,2 17,9 6,4	34,2 21,6 19,7 36,0 22,4 26,2

Задача 2.Используя следующие данные вычислите ранговый коэффициент Спирмена:

№ предприятия	Стоимость основных производст-венных фондов, млн. руб.	Объем валовой продукции, млн. руб.	№ предприятия	Стоимость основных проиводст-венных фондов, млн. руб.	Объем валовой продукции, млн. руб.
	3,8 9,0 2,0 4,9 4,5	5,4 10,9 6,8 8,5 9,3		5,2 3,4 12,0 10,2 12,5	9,8 6,5 15,6 12,9 16,4

Задача 3.Экзаменационная сессия студентов заочников по специальным дисциплинам характеризуется следующими данными:

Студенты	Получившие по всем специальным дисциплинам положительные оценки	Получившие неудовлетво-рительные оценки	Итого
Работающие по специальности Не работающие по специальности
Итого

Рассчитайте коэффициенты ассоциаций и контингенций. Сформулируйте выводы, вытекающие из анализа полученных коэффициентов.

Задача 4. В зависимости от интенсивности полива распределение 130 участков риса по урожайности характеризуются следующими данными:

Урожайность	Полив	Итого
	обильный	средний	слабый
высокая средняя низкая

Рассчитайте коэффициент взаимной сопряженности Пирсона, дайте объяснение полученной величине коэффициента.

Контрольные вопросы

1. Определите понятие - статистическая связь.

2. Какие Вы знаете формы статистической связи?

3. Какие Вы знаете методы изучения статистической связи?

4. Назовите известные Вам показатели тесноты связи.

5. Что такое уравнение регрессии?

6. Каковы предельные значения корреляционного отношения?

7. На что указывает алгебраический знак у коэффициента корреляции?

8. Что такое множественная корреляция?

Тема 6. Ряды динамики

Методические указания

В этой теме рассматриваются приёмы статистического изучения изменения размеров социально-экономических явлений во времени и показатели, измеряющие степень этого изменения. Динамика общественных явлений находит свое цифровое отражение в динамических (хронологических, временных) рядах статистических показателей. Начиная изучение темы, обратите внимание на классификации рядов статистических показателей динамики, которая соответствует классификациям самих показателей. Построение, обработка и анализ этих рядов во многом определяются их особенностями. В этом можно легко убедиться, в частности, на примере расчета аналитических показателей рядов динамики (абсолютных приростов, темпов роста и т.п.). Выяснение сущности этих показателей, их взаимосвязей, методов расчета - необходимое условие усвоения данной темы. Особое внимание следует уделить методам расчета средних показателей рядов динамики, в частности, среднего темпа роста.

Приведём в качестве примера показатели, характеризующие динамику выплавки чугуна в стране за годы XI-ой пятилетки: (1980г. – база пятилетнего плана – y_о = 107,0 млн. тонн):

Годы	Выплавка (млн. т.)	Изменение выплавки (в %) по сравнению	Прирост выплавки по сравнению с предыдущим годом	Прирост выплавки по сравнению с 1980 г.	Абсолютное значение прироста (млн. т.)
		С предыдущим	С 1980 г.	млн. т.	%	млн. т.	%
		100,9	100,9	+1,0	+0,9	+1,0	+0,9	1,07
		99,1	100,0	-1,0	-0,9			1,08
		102,8	102,8	+3,0	+2,8	+3,0	+2,8	1,07
		100,9	103,7	+1,0	+0,9	+4,0	+3,7	1,10
		100,9	104,7	+1,0	+0,9	+5,0	+4,7	1,11

Таблица содержит семь колонок расчётных показателей. В ней приведены:

1) Темпы роста с переменной базой сравнения – цепные (гр. 1) e с постоянной базой сравнения - базисные (гр. 2) (в качестве переменной базы выступает уровень предыдущего года, постоянной - уровень 1980 г.);

2) Абсолютные приросты (гр. 3 – цепные, гр. 5—базисные);

3) Относительные приросты – темпы прироста (гр. 4 - цепные, гр. 6 - базисные);

4) Абсолютное значение % годовых, т.е. цепных приростов - гр. 7

Надо научиться вычислять и средние характеристики рядов динамики: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Покажем методику их исчисления на рассматриваемом примере.

Средний уровень ряда (средняя хронологическая). Среднегодовая выплавка чугуна за годы XI-ой пятилетки:

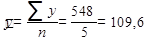млн. т.

Средний абсолютный прирост выплавки чугуна за пятилетку:

млн. т.

Средний темп роста. Среднегодовой темп роста выплавки чугуна в СССР за годы XI-iй пятилетки (расчет показан в 3 вариантах):

(1)

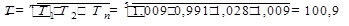
(2)

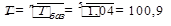
(3)

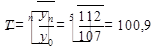
Средний темп прироста получим, вычитая из среднего темпа роста 100%: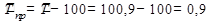

Каждый из рассмотренных показателей динамики характеризует одну eз сторон процесса изменения уровней во времени, в связи с чем эти показатели дополняют друг друга и должны использоваться в анализе динамики совместно, в комплексе.

Показатели динамики тесно связаны со структурным строением объекта. Можно показать, что связь между отчетной и базисной структурами математически выражается посредством темпов роста следующей формулой:

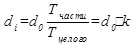
где d – удельный вес части в отчётном (1) e базисном (0) периодах;

k – коэффициент опережения (отставания).

Приведем пример. Удельный вес городского населения области составлял на начало 1940 г. - 33%. Определить, какой величины он достиг к 1988 г. если численность городского населения возросла за это время в 2,155 раза, а общая численность населения области увеличилась на 24,5%. Поскольку городское население (часть) увеличивалось быстрее целого (всего населения) его удельный вес повысился по сравнению с 1940 г. и составил на начало 1988 г.:

Следующей проблемой изучения динамики является выявление основной тенденции, т.е. главного направления в изменении изуча­емого явления. Речь идет о случаях скрытой тенденции, присущей тому или иному ряду динамики. Например, за колебаниями уровней урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистически.

Из различных методов выявления тенденции, обычно рассматриваемых в учебной литературе (укрупнение интервалов, механическое сглаживание, аналитическое выравнивание), обратите особое внимание на последний. Необходимо учитывать, что аналитическое выравнивание представляет собой частный случай применения метода регрессий к анализу социально-экономических явлений. Этот метод заключается в том, что уровни ряда динамики представляются как функция времени (t):

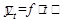
В качестве примера произведем выравнивание приведенных выше показателей о выплавке чугуна в стране за годы одиннадцатой пятилетки по уравнению прямой: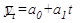

Таблица исходных и расчетных данных

Годы	Выплавка чугуна (млн.т)	t	t2	yt	(млн. т.)
		-2		-216	109,36
		-1		-107	109,48
					109,60
		+1		+111	109,72
		+2		+224	109,84
Итого				+12	548,0

Пояснения к таблице. Первые две колонки - ряд динамики, подвергаемый выравниванию, дополняется колонкой, в которой показана система отсчета времени "t". Причем эта система выбирается таким образом, чтобы .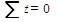

Если число уровней ряда четное, то вместо нуля в центре поставили бы единицы с противоположными знаками у двух уровней, находящихся в середине ряда. Тогда разница между годами составляла бы две единицы времени и общий вид систем был бы таким (например, для ряда из 6 уровней):

-5	-3	-1	+1	+3	+5

В случае применения упрощенной системы отсчета времени параметры уравнения находятся по упрощенным формулам:

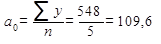
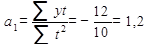
Таким образом, уравнение, выражающее тенденцию роста выплавки чугунав СССР за годы XI-й пятилетии, имеет вид:

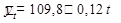
На основе этого уравнения находятся выровненные годовые уровни путем подстановки в него соответствующих значений "t" (они показаны в последней колонке таблицы, причём общий объём выплавки чугуна за всю пятилетку остался неизменным).

Задача 1. Вычислите цепные и базисные абсолютные приросты, темпы роста и прироста, а также абсолютные значения 1% прироста по следующим данным:

Годы
Валовый сбор зерновых культур в СССР (млн. т.)	140,1	223,8	195,7	237,4	179,3	189,1

Задача 2. По данным задачи №1 рассчитайте средние показатели ряда динамики за годы XI-ой пятилетки, средний валовый сбор, средний абсолютный прирост валового сбора, средний темп роста и прироста.

Задача 3. По данным задачи №1 произведите выравнивание по прямой ряда динамики о валовом сборе зерновых в СССР.

Задача 4. Темпы роста выпуска изделия "А" в отрасли составили: в 1986 г. - 102%. 1967 р. - 103%. 1988 г. -104%. Определите средний городской темп прироста за 1986-1988 гг.

Ответ: 2,9%

Задача 6. Планом предусмотрен прирост объема производства предприятия на 50%. Определите среднегодовой темп прироста.

Ответ: 8,4%

Задача 7. Удельный вес мужчин в общей численности населения города составил на начало 1986 г. 46,2%, что на 1,7 процентных пункта меньше чем на 1 января 1981 г. Определите темп роста мужского населения, если общая численность населения за пять лет возросла на 26,8%.

Ответ: 122%

Задача 8. На сколько процентов увеличится производительность труда работников предприятия за три года, если ежегодно она будет возрастать на 2,5%.

Ответ: 7,7%

Задача 9. Сколько средних темпов прироста можно рассчитать по следующим данным о производстве продукта "А" (шт.):

		I960
СССР
РСФСР

Ответ: не менее 42.

Задача 10. Произведите обработку ряда динамики государственных закупок картофеля по СССР методом: 1)укрупнения интервалов; 2)скользящей пятичленной средней:

Годы						I976
Закупки картофеля млн. т.	11,5	11,1	15,4	11,2	14,5	13,4	17,1	15,0	16,4	11,1

Задача 11. Рост выпуска продукции на предприятии в 1988-1992 гг. характеризуется следующими данными:

Год
Продукция, млн. руб.	11,2	12,4	14,8	18,5	21,5

На основе этих данных исчислите: 1) показатели ряда динамики (абсолютный прирост, темп роста и темп прироста, абсолютное значение одного процента прироста); 2) средний уровень ряда; 3) среднегодовой темп динамики (по абсолютным уровням ряда и по коэффициентам роста).

Задача 12. По одному предприятию имелись следующие показатели:

Показатель	Квартал
	I	II	III	IV
Производственный персонал на конец квартала, тыс. чел.	5,8	6,2	6,0	5,9
Заработная плата за квартал, тыс. руб

На основе этих данных: 1) определите вид каждого ряда динамики и их средний уровень (численность персонала на 1.I составила 5,6 тыс. человек); 2) образуйте производный ряд динамики средней заработной платы (в рублях) для каждого квартала; 3) исчислите по каждому показателю темпы динамики во II, III и IV кварталах и среднеквартальный темп.

Задача 13. Ежегодные темпы прироста продукции составили (в процентах к прошлому году):

5,8	6,2	5,6	7,0	6,5

Исчислите за приведенные годы базисные темпы динамики по отношению к 1988 г. и среднегодовой темп прироста за 1988-1992 гг.

Задача 14. Каковы должны быть в среднем ежегодные темпы прироста, чтобы продукция за три года выросла с 50 до 60 млн. руб.

Контрольные вопросы

1. Приведите примеры моментных радов динамики с абсолютными конкретными и абсолютными средними абстрактными уровнями.

2. Приведите примеры интервальных рядов динамики именованных относительных величин, а также интервальных рядов, выражен­ных отвлеченными относительными числами.

3. Назовите аналитические показатели ряда динамики.

4. Что характеризует; a) средняя хронологическая, б) средний темп роста?

5. Какая разница между механическим сглаживанием и аналитическим выравниванием ряда динамики?

6. Что показывают индексы сезонности и как они исчисляются?

Тема 7. Индексы

Тема "Индексы" - одна из важнейших тем курса. В ней излагается сущность и общие приёмы построения специфических статистических показателей - экономических индексов. Без усвоения общих правил и принципов построения индексных показателей невозможно правильное применение их в конкретных случаях демографического и экономико-статистического анализа. Поэтому важно усвоить прежде всего общие вопросы индексологии: сущность индекса, его составные элементы, твёрдо запомнить, что основными вопросами построения сводных индексов являются вопросы выбора соизмерителей и весов конкретных индексов, Решаются эти вопросы на основе экономической теории.

В отечественной статистике принято правило: индексы качественных показателей строятся с весами отчётного периода, индексы количественных показателей - с весами базисного периода.

Особенностью темы является широкое применение условных обозначений экономических показателей: например, цены обозначаются обычно через "P": P₀ – для базисного периода; Р₁ - для отчетного; количество товаров (продукции) – соответственно через q₀ и q₁.

В теме рассматриваются важные вопросы построения динамических рядов индексных показателей, что связывает её с предыдущей темой.

Следует подчеркнуть, что специфическим вопросом построения цепных и базисных индексов является выбор веса системы индексов – постоянного для всех показателей системы, либо индивидуального для каждого из них (индексы с постоянными и переменными весами).

Необходимо уделить особое внимание индексному методу изучения динамики среднего уровня, когда общий индекс исследуемого явления, строящихся как отношение средних величин показателя за отчетный период и базисных (индекс переменного состава), разлагается на частные индексы - индекс фиксированного состава и индекс влияния структурных сдвигов на динамику среднего уровня, или короче - индекс структуры. Важно понять, что возможность применения индекса переменного состава появляется только тогда, когда можно для изучаемого явления вычислить среднюю величину.

Большое значение для правильного понимания основных проблем темы имеет разбор вопросов, связанных с критикой формально-математической трактовки индексов в буржуазной статистике.

Приведем примеры на расчет индексов.

Пример 1. Рассчитать индивидуальные и общие индексы товарооборота, физического объема проданных товаров и цен по следующим данным о ценах и реализации товаров за два месяца:

	Январь	Февраль	Индексы
Товары	цена (руб.)	Реализация	цена (руб.)	Реализация	цен	Физического объема продажи	Товаро-оборота
		кг	руб.		кг	руб.
А	1,0			0,8
Б	0,5			0,5
В	0,2			0,3
Итого	-	-		-	-		87,7	102,7	90,3

Индивидуальные индексы, характеризующие динамику показателей по каждому товару, помещены в графах 7,8,9 таблицы по строкам А, Б, В. Они легко получаются путем сравнения соответствующих показателей за январь и февраль (например, индекс цен по товару "А" i_p = P_I : P₀ = 0,8:1,0 = 80%. Сводные индексы записаны по итоговой строке этих колонок. Они рассчитаны следующим образом:

Индекс цен: 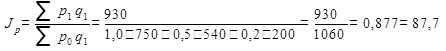, т.е. в целом цены снизились на 12,3%.

Из формулы следует, что индекс цен есть отношение стоимос­ти товаров отчётного периода к стоимости тех же товаров, но по базисным (у нас январским) ценам. Снижение цен привело к удешевлению массы товаров, проданных в феврале в абсолютном выражении на сумму 130 руб. (1060-930).

Индекс количества проданных товаров (физического объёма товарооборота) рассчитывается как отношение товарооборота отчетного периода по базисным ценам e товарообороту базисного периода: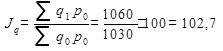

Следовательно, фактический объём продажи возрос на 2,7%.

Индекс товарооборота (стоимости проданных товаров) может быть получен двумя способами:

1) по формуле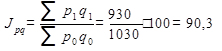

2) на основе рассчитанных индексов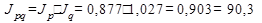

Пример 2. По следующим данным определить общий индекс цен на товар "А" в двух формах: как индекс фиксированного и пе­ременного состава. Определить влияние структурных сдвигов на динамику средней цены:

Рынки	Цена за 1 кг товара (руб.)	Продано кг товара	То же в % к итогу
	1 кв.	2 кв.	1 кв.	2 кв.	1 кв.	2 кв.
№ 1	1,5	1,2
№ 2	1,0	1,0

Индекс цен фиксированного состава рассчитаем по уже известной формуле: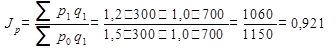

Этот индекс показывает, что за счет изменения цен на отдельных рынках цена на товар "А" в целом во 2-м квартале стала ниже на 7,9%.

Индекс цен переменного состава получается как отношение средней цены двух сравниваемых периодов:

Таким образом, снижение цен составляет уже 15,2%. Расхождение этих двух индексов - результат изменения структуры продажи (см. две последние колонки таблиц). Действительно, - если в первом квартале удельный вес рынков в общей продаже товара "А" совпадал, то во 2-м квартале основной объем продажи (70%) приходился на 2-ой рынок, где цены более низкие, -что и предопределило дополнительно снижение средней цены. Размер этого снижения найдём путем деления второго индекса на первый:

Индекс влияния структурных сдвигов

=

Индекс переменного состава

:

Индекс постоянного состава

= 0,848 : 0,921 = 0,920

Рассмотренные индексы можно представить несколько в другом виде, заменив "q" через "d" (где , причём ), т.е. используя вместо абсолютных данных относительные (помещённые в двух последних столбцах таблицы).

Тогда индекс переменного состава можно представить так: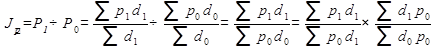

Таким образом, индекс переменного состава разложен на два частных индекса, выражающих роль отдельных факторов - динамику изменения цен (первый сомножитель) и динамику структурных изменений (второй сомножитель).

Следовательно, задача может быть решена непосредственно по этим формулам:

1) индекс цен переменного состава (динамика средней):

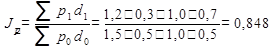
2) индекс цен фиксированного состава (средняя динамика):

3) Индекс влияния изменения структуры на динамику средней цены товара "А".

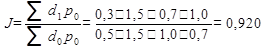
Задача 1. Рассчитайте индексы цен, физического объёма товарооборота и товарооборота по следующим данным:

Товары	Цена на единицу товара (руб.)	Реализовано единиц
	1 кв.	2 кв.	1 кв.	2 кв.
А	0,30	0,25
Б	1,3	1,2

Ответы: 38,4; 113,6 и 100,4%

Задача 2. Рассчитайте сводный индекс цен на основе следующих данных;

Товары	Индексы цен (%)	Товарооборот отчетного периода (тыс. руб.)
А
Б
В

Ответ: 101,21%

Задача 3. Рассчитайте общий индекс физического объема продукции по следующим данным;

Изделия	Изменение выпуска в отчетном периоде по сравнению с базисным (%)	Удельный вес изделия в общем выпуске базисного периода (%)
А	+5
Б	-5

Ответ: 101 %

Задача 4. Рассчитайте индексы производительности труда переменного и постоянного состава. Определите индекс влияния структурных сдвигов на динамику средней выработки.

Шахты	Базисный период	Отчетный период
	Добыча угля (млн. т.)	Число работников (тыс. чел.)	Добыча угля (млн. т.)	Число работников (тыс. чел.)
№ 1	1,6		2,7
№ 2	1,3		1,4

Ответы: 120,6%; 114,1%; 105,7%.

Задача 5. Рассчитайте индексы физического объема продукции: плановый на 1986 г., фактический за 1986 г., и определите степень выполнения плана по следующим данным:

Изделия	Выпуск (тыс. штук)	Отпускная цена единицы на 01.01.85 (руб.)
	1985 г.	1986 г.
		план.	факт.
А
Б

Ответ: 110,1%; 114,7%; 104,1%

Задача 6. По заводу имеются следующие данные о выработке и отпускных на продукты за два периода:

Наиме-нование продуктов	Единица измерения	Базисный Выработано единиц	период Цена за единицу, коп.	Отчетный Выработано единиц	период Цена за единицу, коп.
А Б В	м шт. кг

Исчислите по заводу в целом; 1) агрегатный индекс отпускных цен и размер экономии от снижения цен, 2) агрегатный индекс физического объема продукции.

Задача 7. По следующим данным исчислите общий индекс физического объема продукции:

№ заводов	Валовая продукция базисного периода, тыс. руб.	Рост производства в планируемом периоде по сравнению с отчетным, %
		140,0 90,0 120,0

Задача 8. Товарооборот по молочным продуктам увеличился в апреле по сравнению с мартом на 4%, а цены снижены за этот же месяц на 15%. Как изменилось количество проданных молочных продуктов в апреле по сравнению с мартом?

Задача 9. Выручка от реализации на рынке возросла на 10% при увеличении объема продажи овощей на 22%. Как изменились цены на овощи?

Задача 10. Общие затраты на производство по заводу возросли в отчетном периоде по сравнению с базисным на 20% при увеличении объема производства на 25%. Как изменилась в отчетном периоде по сравнению с базисным себестоимость единицы продукции?

Задача 11. Численность рабочих увеличилась на 25%, фонд заработной платы - на 30%. Как изменилась средняя заработная плата одного рабочего?

Задача 12. На одном предприятии стоимость продукции составила в базисном году 2,4 млн. руб., а в отчетном - 2,76 млн. руб. Число работающих соответственно составило 300 и 315 человек. Определите, на сколько процентов прирост продукции был обеспечен ростом производительности труда.

Контрольные вопросы

1. Дайте определение сводного индекса.

2. Назовите формы сводного индекса.

3. В чем отличия индексов с переменной и постоянной базой сравнения от индексов с постоянными и переменными весами?

4. Как связаны между собой цепные и базисные индексы?

5. Что такое индекс переменного состава?

6. Чем отличаются территориальные индексы от динамических?

7. Напишите формулы конкретных индексов, которые Вы знаете.