Методы оценки стоимости и доходности финансовых активов с фиксированным доходом

С фиксированным купоном

Купонные облигации. предусм. возврат основ. суммы + периодич-кие выплаты. Размер этих выплат опред. ставкой купона и выраж в %-х к номиналу.

Периодичность купонных выплат:

-1р. в год

-2р. в год

4р. в год

Классич пример подобных цб:

-облигации внутр. валютн. займа – ОВВЗ

-облигации федерального займа – ОФЗ

- ряд корпоративных долговых обяз-в

Периодические выплаты по фиксиров. ставке

Доход по куп. облигац. им. 2 сост-щие:

-периодические выплаты

-курсовая разница м/д ценой и номиналом

В связи с этим такие облиг. хар-ся неск. показ-ми доходности:

-купонной

-текущей (на момент приобрет)

-полная (к погашению)

Купонная доходность задается при выпуске облигаций и опред-ся соотв. %-й ставкой. Величина купонной доход-ти зависит от 2-х факторов:

-от срока займа

-от надежности эмитента

Чем выше срок погашения, тем выше её риск, тем выше д/б норма доходности, кот. требует инвестор в кач-ве компенсации.

Важ. фактор – надеж. эмитента, опред. кач-во (рейтинг) облигации.

Самый надежн. – гос-во, т.к. ставка купона ниже, чем у корпорат-ой.

Купон. дох-ть облигации при фиксир. ставке известна заранее, и остается неизменной на протяжении всего срока обращения.

Ех.: Опред. велич. ежегод. дох. по облиг. номин. в 1000р. при условии, что купон. ставка =8%.

Если облигац. покуп. или прод. в момент м/д 2-я купон. выплатами, то важн. значение имеет показатель величина накопительного купонного дохода (к дате операции) – НКД.

Механизм формирования доходов продавца и покупателя д/сделки, заключ. м/д 2-я купонными выплатами, рассматр-ся на примере.

Ех.: Облигация с номиналом 100 т.р. выпущена 10.04.96, продана 18.03.97. Дата предыдущ. выплаты купона 10.04.97. Текущ. купон 33,33% годов. Выплаты 4 р. в год.

1.Абсол. величина купон. дох.:

CF=100т.р.*(0,3333/4)=8332,50 р.(доход покуп. на 10.04.97)

2.Накопл. куп. доход:

NKD=(N*k*t)/(B/m)

k –ставка купона

B – исследуемая врем. база (пр.% - 360, точн.% - 365, 366 дн.)

t – дата от начала купона до его продажи

m – кол-во выплат

NKD=(100т.*(0,333/4)*67)/(360/4)=6203,08 (для продавца)

Продавец м/реализовать свое право на получение КД, включая НКД в цену облигации.

Предположим, что облиг. была куплена по номиналу. Определим курс продажи облигации, обеспечивающий получение части КД пропорциональной сроку хранения.

Курс продажи облиг. для продавца =(100т.+NKD)/100=(100т.+6203,08)/100=1062,03

NKD – величина условная, поэтому мы приближаем полученное число до возможно вероятного. Тогда курс для продавца =106,2%. Т.о. курс продажи д/продавца не д/б меньше этой величины.

NKD для покупателя =CF-NKD для продавца=8332,50-6203,08=2129,42

Курс =106,2% соотв-ет ситуации равновесия, когда и продавец и покупатель получат часть купонного дохода пропорционального сроку хранения облигации.

Текущая доходность (У)

Текущая доходность облиг. с фиксир-й ставкой купона опред-ся как отношение периодического платежа к цене приобретения.

У=((NK)/P)*100=(k/K)*100

P – цена покупки

k – годовая ставка

K – курсовая цена

Текущая дох. продаваемых облигаций меняется в зависимости от рын. цен, но с момента покупки она становится постоянной (фиксированной), т.к. ставка купона остается неизменной.

Ех: Определить тек. дох-ть из предыд. примера, но: облиг. б/приобретена по цене 106,2%

У=((100т.(0,333/4))/106,2)*100=7846,05

Доходность к погашению

Дох-ть к погашению - % ставка или норма дисконта устанавливающая равенство м/д текущей ст-тью потока платежей по облиг. и ее рын. ценой.

УТМ=((CF+(F-P))/n)/(0,4F+0,6P)

F – цена погашения

Р – цена покупки

Св-ва УТМ:

1.Дох. к погаш. – это % ставка в норме дисконта, кот. приравнивает величину потока платежей к текущей рын. ст-ти облигации. По существу УТМ представл. собой внутр. норму доходности инвестиции. Этот показатель обладает рядом недостатков, связанных с тем, что реальная доходность облиг. к погашению будет справедливо определена только в том случае, если облигация хранится до срока погашения и, если полученные купонные доходы будут реинвестированы по ставке = доходности к погашению.

Результаты расчета доходности к погашению облигации, приобретенной в момент выпуска по номин. в 1000р. с погашением через 20 лет и ставкой купона =8%, выплачив-го 1р. в год при различных ставках реинвестирования.

Ставка реинвестир-я (%)	Купонный доход за 20 лет	Общий дох. по облиг. за 20 лет	Дох-ть к погашению (%)
			4,84
			7,07
			8,0
			9,01

М/д дох. к погашению и ставкой реинвестирования всегда сущ-ет прямая зависимость, т.е. с увеличением ставки реинвест. растет дох. к погашению, и наоборот.

На величину дох. к погашению влияет и цена облигации.

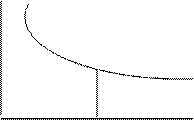На графике зависимости дох-ти к погашению от цены д/обл. со сроком погашения 25 лет и ставкой купона 6%.

Сущ-ет обратная зависимость м/д доходностью к погашению и ценой облигации.

Общие правила, отражающие взаимосвязь м/д ставкой купона, текущей доходностью, доходностью к погашению и ценой облигации:

1.Если P>N, то K>У>УТМ

2.Если P<N, то K<У<УТМ

3.Если Р=N, то K=У=УТМ

Несмотря на свою условность показатель дох-ть к погашению явл. одним из самых популярных измерителей доходности облигаций и его значения приводятся во всех фин. сводках и аналит-х обзорах.

Ст-ть облигаций с фиксир. купоном

Ден. поток, кот. генерирует с обл. с фиксир. ден. купоном представляет собой аннуитет, к кот. в конце срока операции прибавляется номин. ст-ть обл., пересч. с коэфф. наращения (дисконтирования):

PV= ^nm∑_t=1 (((N*k)/m)/(1+r/m)^t+F/(1+r)^nm)

F – сумма погашения (часто равен номиналу – F=N)

r – рын. ставка или норма дисконта

n – срок обращения облигации

m – кол-во купонных выплат

N - номинал

Ех.: Определить текущ. ст-ть 3-летней облигации с номиналом =1000р. и купонной ставкой 8%, выплач-х 4 р. в год при условии, что норма дисконта =12%.

PV=∑((1000*0,08)/(1+0,12/4)¹+1000/(1+0,12)^4*3)=334,08

Чем норма дисконта выше, тем текущая ст-ть ниже.

1-я группа Теорем, кот. отражает взаимосвязь м/д ст-тью облигаций, ставкой купона и рын. ставкой.

1-я теорема: Если рын. ставка выше ставки купона, то текущая ст-ть облиг. будет меньше номинала (в этом случае облигация будет продаваться с дисконтом).

2-я теорема: Если рын. ставка (норма доходности) меньше ставки купона, то текущ. ст-ть облигации будет больше номинала (облиг. будет продаваться с премией).

3-я теорема: При равенстве купонной и рын. ставок текущая ст-ть облиг.= номиналу.

2-я группа теорем хар-ет связь м/д ст-тью облиг. и сроком её погашения.

1-я теорема: Если рын. ставка выше ставки купона суммы дисконта по облигации будет уменьшаться по мере приближения момента погашения.

2-я теорема: Если норма доходности меньше ставки купона, то величина премии будет уменьшаться по мере момента погашения.

3-я теорема: Чем больше срок обращения облигации, тем чувствительнее её цена к рын. ставке.