Наращенная сумма аннуитета постнумерандо

Денежные потоки

Виды денежных потоков

Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени, например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплаты пенсий и т.д. Такого рода последовательность или ряд платежей называют потоком платежей. Отдельный элемент такого потока называется членом потока.

Потоки платежей могут быть регулярными (размеры платежей постоянные или следуют установленному правилу, предусматривающему равные интервалы между платежами) и нерегулярными. Члены потоков могут быть как положительными (поступления), так и отрицательными (выплаты) величинами.

Поток платежей, все члены которого – положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой (рентой) или аннуитетом. Рента описывается следующими параметрами: член ренты – размер отдельногоплатежа, период ренты – временной интервал между двумя последовательными платежами, срок ренты – время от начала первого периода ренты до конца последнего, процентная ставка.

Классификация рент:

1) По количеству выплат членов ренты на протяжении года:

· Годовые – выплата раз в году;

· Р – срочные (р – количество выплат в году).

2) Ренты с периодами, превышающими один год – дискретные.

3) Потоки платежей поступающие так часто, что их рассматривают как непрерывные.

4) По числу начислений процентов на протяжении года:

· Ренты с ежегодным начислением;

· С начислением m – раз в году;

· С непрерывным начислением.

5) По величине своих членов

· Постоянные – с одинаковыми размерами членов ренты;

· Переменные.

6) По вероятности выплат

· Верные;

· Условные.

7) По количеству членов

· Ограниченные – с конечным числом членов, их срок заранее оговорен;

· Вечные ренты.

8) По соотношению начала срока ренты и какого-либо момента времени, утверждающего начало ренты:

· Немедленные;

· Отложенные или отсроченные.

9) Различия по моменту выплат платежей в пределах периода ренты:

· Обыкновенные или постнумерандо – платежи осуществляются в конце периодов;

· Пренумерандо – платежи осуществляются в начале периодов.

В подавляющем числе случаев анализ потока платежей предполагает расчет одной из двух обобщающих характеристик:

§ Наращенной суммы – суммы всех членов потока платежей с начисленными на них к концу срока процентами.

§ Современной стоимости потока платежей – суммы всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.

Оценка денежного потока может исполняться в рамках решения двух задач:

1. Прямой, т.е. проводится оценка с позиции будущего (реализуется схема наращения). Прямая задача предполагает суммарную оценку наращенного денежного потока, т. е. в ее основе лежит будущая стоимость. В частности, если денежный поток представляет собой регулярные начисления процентов на вложенный капитал Р по схеме сложных процентов, то в основе суммарной оценки наращенного потока лежит формула:

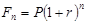
(6.1)

или, что то же самое, если имеется ряд платежей R_t, выплачиваемых спустя время n_t после некоторого начального момента времени. Общий срок выплат n лет, необходимо определить наращенную сумму:

(6.2)

2. Обратной, т.е. проводится оценка с позиции настоящего (реализуется схема дисконтирования). Обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока. Приведение денежного потока к одному моменту времени осуществляется с помощью формулы:

(6.3)

Пример 1.

График предусматривает следующий порядок выдачи ссуды во времени: 1июля 2004 г. – 5млн. руб., 1января 2005г. – 15 млн. руб., 1января 2007 г. – 18 млн. руб. Необходимо определить сумму задолженности на начало 2008 г., а также современную стоимость потока на момент выплаты первой суммы при условии, что проценты начисляются по ставке 20% годовых.

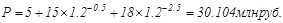
при прямом счете

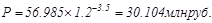
Аннуитеты постнумерандо

Наращенная сумма аннуитета постнумерандо

Годовая рента. Пусть в течение n лет в банк в конце каждого года вносится по R рублей. На взносы начисляются сложные проценты по ставке r % годовых. Все члены ренты приносят проценты, кроме последнего, - на первый член проценты начисляются n-1 год, на второй n-2 и т.д. На последний взнос проценты не начисляются. Размер наращенной суммы к концу срока составит:

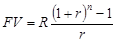(6.4)

Обозначим множитель, на который умножается R, через F_n;r, нижний индекс n;r указывает на продолжительность ренты и величину процентной ставки. Далее этот множитель будем называть коэффициентом наращения ренты. Данный коэффициент представляет собой наращенную сумму ренты, член которой равен 1:

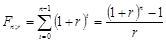(6.5)

Таким образом,

(6.6)

Пример 2.

Для обеспечения некоторых будущих расходов создается фонд. Средства в фонд поступают в виде годовой ренты постнумерандо в течение 5 лет. Размер разового платеже равен 4 млн. руб. На поступившие взносы начисляются проценты по ставке 18,5% годовых. Определить величину фонда на конец срока.

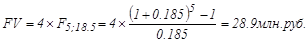
Годовая рента с начислением процентов m раз в году. Число членов ренты равно nm. Размер наращенной суммы составит:

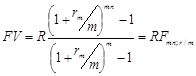(6.7)

Пример 3.

Несколько изменим условия примера №2. Пусть теперь проценты начисляются поквартально, а не раз в году.

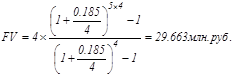
Рента p – срочная (m=1). Пусть рента выплачивается p раз в году равными суммами, процент начисляется один раз в конце года. Если годовая сумма платежей равна R, то каждый раз выплачивается R/p. Общее число членов ренты равно np. Размер наращенной суммы составит:

(6.8)

Пример 4.

Вернемся к условиям примера №3. Платежи теперь выплачиваются поквартально:

Рента р - срочная (p=m).В данном случае число выплат в году равно числу начислений процентов: p=m. Размер наращенной суммы составит:

(6.9)

Рента p – срочная (p≠m).Определим теперь наращенную сумму для наиболее общего случая – p – срочная рента с начислением процентов m раз в году. Общее количество членов ренты равно np, величина члена ренты R/p. Размер наращенной суммы составит:

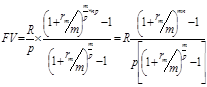(6.10)

Пример 5.

Если в ренте, наращенная сумма которой определялась в примере №4, начисление процентов производится ежемесячно, то

Непрерывное начисление процентов. Существуют ренты с непрерывным начислением процентов. Размер наращенной суммы в этом случае составит:

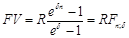, где e – основание натуральных логарифмов.

Аналогично для p – срочной ренты с непрерывным начислением процентов находим:

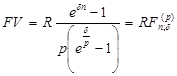(6.11)

Пример 6.

Если бы в условиях примера №2 вместо ежегодного начисления процентов предусматривалось непрерывное их начисление, причём сила роста равна 18,5%, то

При ежеквартальной выплате членов ренты получим