Финансово-математические основы инвестиционного проектирования

Для оценки инвестиционных проектов применяются финансовые вычисления, которые базируются на понятии временной стоимости денег.

Концепция стоимости денег во времени: рубль, полученный сегодня, стоит больше, чем рубль, который будет получен в будущем.

Различие между равными по абсолютной величине суммами денежных средств, получаемых в различные периоды времени, называется временной стоимостью денег.

При этом параметр «временная ценность денег» рассматривается в двух аспектах: первый связан с обесцениванием денежной наличности с течением времени: второй — с обращением капитала (денежных средств).

Основная причина данного экономического феномена кроется в уменьшении покупательной способности денежных средств. Однако наряду с инфляционным обесцениванием денег существуют и другие причины.

1. Немедленное удовлетворение потребностей для человека важ­нее, чем удовлетворение их в будущем.

2. Существует риск неполучения «завтрашних» денег, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого «завтра».

3. Располагая денежными средствами «сегодня», экономический субъект может их разместить на финансовом рынке (вложить в какое-нибудь доходное предприятие) и получить дополнитель­ный доход.

4. Разумный человек стремится выбрать наиболее ликвидную форму имеющихся у него финансовых активов, а любые обяза­тельства, получаемые им взамен денег, имеют более низкую лик­видность. Таким образом, у кредитора возрастает риск потери лик­видности.

Естественно, большинство владельцев денег не согласны бес­платно принимать на себя дополнительные риски. Платой за риск должна стать дополнительная прибыль. Поэтому, предоставляя кредит, владельцы денег устанавливают такие условия его возврата, которые возместят им все возникающие неудобства. Количественной мерой величины этого возмещения является процентная ставка.

Экономисты выделяют два типа экономического мышления и соответствующих им подходах к анализу явлений и процессов:

• статический подход, который не учитывает фактор времени. Здесь возможно оперирование денежными показателями, относящимися к различным периодам времени, и их суммирование;

• динамический подход, который учитывает фактор времени. Здесь неправомерно суммировать денежные величины, относящиеся к различным моментам времени.

В рамках динамического подхода одну и ту же сумму денег не­обходимо рассматривать с двух позиций: с позиции ее настоящей и будущей стоимости.

С помощью процентной ставки может быть определена как будущая стоимость «сегодняшних» денег (та сумма, в которую превратятся инвестированные в настоящий момент денежные средства через определенный период времени с учетом определенной процентной ставки), так и настоящая — современная, текущая или приведенная стоимость «завтрашних» денег, т.е. сумма будущих денежных поступлений, приведенных к настоящему моменту времени с учетом определенной процент­ной ставки.

Поскольку инвестирование представляет собой обычно длительный процесс, в инвестиционной практике применяется динамический подход.

Элементы теории процентов

Основу коммерческих вычислений составляют ссудозаемные операции, в которых ярче всего проявляется необходимость учета временной ценности денег.

Процентные ставки по депозитным вкладам и заемным средствам часто являются базой (отправной точкой) при определении нормы дисконта. Кроме того, принимая во внимание, что использование норм дисконта, учитывающих инфляционные ожидания инвесторов, является одним из методов учета инфляции при инвестиционном анализе, необходимо обратить внимание на такую экономическую категорию, как процентные ставки.

Процентной ставкой (rate of interest) называется относительный (в процентах или долях) размер платы за пользование ссудой (кредитом) в течение определенного времени.

Процентная ставка, взимаемая банком по кредитам, называется кредитной процентной ставкой P_кр. Частным случаем кредитной процентной ставки является ставка рефинансирования Центробанка. Это ставка процента, под который Центробанк выдает коммерческим банкам кредит для пополнения их резервов.

Процентная ставка, выплачиваемая банкам по депозитным вкладам, называется депозитной процентной ставкой P_д. Кредитная и депозитная процентные ставки могут быть номинальными, реальными и эффективными.

Номинальной (nominal interest rate) называется процентная ставка P_н, объявленная кредитором. Она учитывает, как правило, не только доход кредитора, но и индекс инфляции. Все объявленные банками ставки являются номинальными. Номинальная процентная ставка рассчитывается:

N=R+I (темп инфляции на финансовом рынке)

Реальная процентная ставка (real interest rate) P₀ – это номинальная процентная ставка, приведенная к неизменному уровню цен, т.е. скорректированная с учетом инфляции («очищенная от инфляции»). При невысоких темпах инфляции 3-5% в год реальная рассчитывается как R=N - I

При более высоких темпах инфляции взаимосвязь между номинальной и реальной ставками становится нелинейной. Связь между номинальной и реальной процентными ставками дается формулой Фишера:

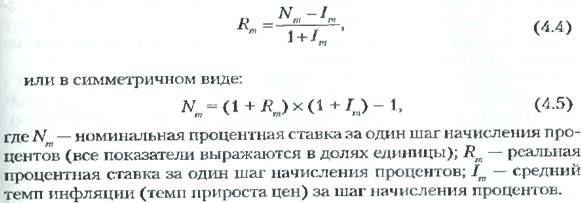
Эффективная процентная ставка P_ef характеризует доход кредитора за счет капитализации процентов, выплачиваемых в течение периода, для которого объявлена номинальная процентная ставка.

Так, если номинальная процентная ставка за год равна P_н (в долях единицы), а выплата процентов по условию займа происходит m раз в год, то практически всегда банк определяет процент при каждой выплате равным P_н/m. В этом случае эффективная процентная ставка P_ef (в долях единицы) определяется по формуле

Простая процентная ставка — ставка, при которой доход каж­дый раз начисляется на первоначально вложенную сумму. Форму­ла простых процентов имеет следующий вид:

то ,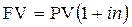

где FV — сумма, которую владелец получит спустя определенное время, или будущая стоимость, PV — сумма, которой владелец обладает сегодня, или современная (текущая) стоимость; i — про­центная ставка; n — период начисления процентов в годах.

ПРИМЕР. Так, если разместить 10000 тыс. р. на 1 год 7 мес под 12% годовых (проценты начисляются по простой ставке), то наращен­ная сумма после 1 года 7 мес будет равняться:

В процессе анализа инвестиционных ре­шений принято использовать сложные про­центы.

Сложная процентная ставка применя­ется к наращенной сумме долга. При этом накопленные проценты добавляются к ос­новной сумме и полученная увеличенная сумма является исходной для начисления процентов в следующем периоде. Формула сложных процентов имеет следующий вид:

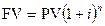
Данную формулу называют стандартной формулой сложного процента, или формулой наращения (компаундинга), или капитализацией процентного дохода.

Суть сложного процента в том, что на наращенные в предыдущем периоде суммы вновь начисляются проценты, т.е. происходит много­разовое наращение. Поэтому компаундинг — рост во времени некото­рой денежной суммы в результате реинвестирования получаемых на нее процентов.

(1+i)ⁿ – коэффициент наращения.

ПРИМЕР. Например, если разместить 10000 тыс. р. на один год 7 мес под 12% годовых (проценты начисляются по сложной ставке), то на­ращенная сумма после 1 года 7 мес будет равняться:

ПРИМЕР (по сложному и простому проценту). Предположим, что мы сегодня можем положить 1000 руб. на депозит под 5 % годовых. Через год сумма на сберегательном счете составит 1050 руб.

В нашем примере будущая стоимость (future value или FV) сегодняшних 1000 руб. при ставке 5 % годовых составит 1050 руб.

,

,

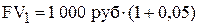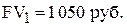
Если мы не будем изымать деньги из банка и оставим их там на второй и третий годы, то окончательная сумма после завершения двухлетнего и трехлетнего периода соответственно составит:

;

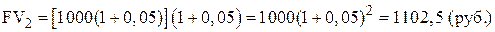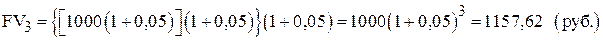
Теперь попробуем решить обратную задачу, т.е. определить текущую (современную) стоимость (PV) (или определение того, сколько надо было бы инвестировать сегодня, чтобы получить некоторую сумму в будущем).

Для осуществления такого расчета используется формула, которая является обратной по смыслу формуле (5.1):

PV= 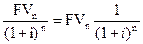. (5.2)

При расчете эффективности инвестиционных проектов используется обычно вместо i E – величина доходности инвестиций, в данном примере она равна ставке банковского процента по сберегательному вкладу, а в более общем случае – прибыльности инвестиций;

Следовательно, текущая (современная) стоимость равна будущей стоимости, умноженной на коэффициент , называемый коэффициентом дисконтирования.

Норма дисконта (Rate of Dicount) – с экономической точки зрения – это норма прибыли, которую инвестор обычно получает от инвестиций аналогичного содержания и степени риска. Таким образом, это ожидаемая инвестором норма прибыли (Opportunity Rate of Return).

Факторы, влияющие на выбор нормы дисконта Е:

— представления инвестора;

—тип инвестиционного проекта (коммерческий, социальный и т.п.);

— депозитный процент по вкладам, доходность государственных долгосрочных облигаций и т.п. (доходность альтернативных, менее рискованных инвестиций);

— источники финансирования (собственные, внешние, заемные и т.п.);

— финансовое состояние участников инвестиционного проекта;

— цели и условия реализации инвестиционного проекта;

— экономическая конъюнктура;

— темп инфляции;

— уровень риска инвестиционного проекта;

— уровень ликвидности инвестиционного проекта и др.

В нашем примере текущая стоимость (PV), т.е. сумма, которую необходимо инвестировать, чтобы через 3 года при 5 % годовых получить 1000 рублей, составит:

Определяя величину текущей стоимости (PV) исходя из суммы будущей стоимости, мы проводим дисконтирование будущей стоимости.

Дисконтированием называется процесс приведения (корректировки) будущей стоимости денег к их текущей (современной стоимости). Процесс, обратный дисконтированию, а именно, определение будущей стоимости, есть не что иное, как начисление сложных процентов на первоначально инвестируемую стоимость, или наращение.

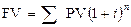
PV=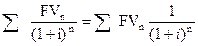

Процессы начисления сложных процентов и дисконтирования являются столь же древними, как и сам процесс кредитования, и используются финансовыми институтами с незапамятных времен.

Коэффициенты дисконтирования не требуется каждый раз считать отдельно, они приводятся в специальных таблицах (если невозможно применение специального программируемого калькулятора).