Будущая стоимость инвестиций

Для расчета будущих величин используется формула сложных процентов:

FV=PV(1+k)ⁿ; (1.1)

где FV – (англ. future value ) – будущая величина той суммы, которую мы инвестируем в любой форме сегодня .; PV – ( англ. present value ) – текущая (современная) стоимость той суммы, которую мы инвестируем ради получения дохода в будущем; k – доходность инвестиций; n – число периодов времени, в течении которых наши инвестиции будут участвовать в коммерческом обороте.

Значение множителя (1+k) можно взять в приложении табл.1.

Финансовые операции, предполагающие ежегодный денежный взнос с целью накопления определенной суммы в будущем, называются аннуитетом (англ. annuity – ежегодный платеж). Окончательная сумма аннуитета определяется по формуле:

FVA_n = 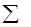PMT_t * (1+k)^n-t; (1.2)

где FVA_n – будущая стоимость аннуитета_, PMT_t - платеж, осуществляемый в конце периода t; k – уровень дохода; n – число периодов получения дохода.

Если сумма платежей одинакова в каждом периоде, формула 1.2 принимает вид:

FVA_n = PMT*FVA1_n;k; (1.3)

где РМТ – годовая сумма денежного потока; FVA1_n;k – будущая стоимость аннуитета 1 рубля в конце каждого периода.

FVA1_n;k = [(1+k)ⁿ–1]/k; (1.4)

Значение этого показателя (FVA1n;k) можно взять из приложения (прил.3).

Пример 1. Вы решили сформировать личный фонд путем откладывания в конце каждого из 30 лет вашей трудовой деятельности по 1000 тыс. руб. на банковский счет со ставкой 10% годовых. Спрашивается сколько средств будет на вашем счете через 30 лет?

FVA₃₀ = PMT FVA1_20;10 = 1000*164,49 = 164490 (руб.)

Может быть обратная задача.

Пример 2. Алюминиевому заводу предстоит через 5 лет заменить установку в 100 тыс. руб. Есть договоренность с банком об открытии накопительного счета со ставкой 10% годовых. Сколько предприятию надо ежегодно перечислять на этот счет?

PMT = FVA₅/FVA1_5;10 (из формулы 1.3)

FVA1_5;10 = 6,105 (см приложение табл. 2) , тогда РМТ = 100 / 6,105 = 16,380 тыс. руб.

Предоставляя долгосрочные кредиты, зачастую банки используют изменяющиеся во времени, но заранее фиксированные для каждого периода процентные ставки. В этом случае наращенная сумма может быть определена по формуле:

FV=PV (1+ k ₁)ⁿ¹(1+ k ₂)ⁿ²х(1+ k ₃)ⁿ³ х…х(1+ k ₁₂)^nk; (1.5)

Где S – наращенная сумма; P – сумма капитала, предоставляемого в кредит; k ₁ , k ₂… k ₁₂ – последовательные значения ставок процентов; n₁, n₂ …n_k - периоды, в течении которых используются соответствующие ставки.

В случае, когда срок финансовой сделки выражен дробным числом, начисление процентов может выполняться по формуле сложных процентов:

FV=PV (1+ k)^a+b; (1.6)

где n=a+b – период сделки; а – целое число лет; b – дробная часть года.

Если в контракте на получение кредита предусматривается капитализация процентов несколько раз в году (по полугодиям, кварталам, помесячно), тогда для определения наращенной суммы применяется следующая формула:

FV=PV (1+ j /m)^N; (1.7)

где j – номинальная годовая процентная ставка; m – число периодов начисления процентов; N – число периодов начисления процентов за весь срок контракта; N=m*n, где n – число лет.

Пример 3. Получен кредит в размере 150 тыс. руб. сроком на два года, под 15% годовых. Начисление процентов производится ежеквартально. Определить наращенную сумму, подлежащую возврату.

FV =150(1+0,15/4)^2*4=150*1,3425=201,37 (тыс. руб.)

Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена по общей формуле, используемой при начислении сложных процентов, или по смешанному методу. В последнем случае наращенная сумма определяется по формуле:

FV=PV (1+j/m)^ml(1+a^j/m); (1.8)

где ml – число полных периодов начисления процентов; а – дробная часть периода начисления процентов.

Текущая стоимость денег

Нахождение текущей (современной) величины денежных потоков на некоторый момент времени производится с помощью дисконтирования. С помощью дисконтирования в финансовых вычислениях учитывается фактор времени. Суть этого метода в следующем:

нахождение текущей величины PV(P) на некоторый момент времени при условии, что в будущем при начислении на неё процентов она могла бы составить наращенную сумму FV(S).

При дисконтировании решается задача, обратная определению наращенной суммы. Она формулируется следующим образом:

Какую сумму необходимо инвестировать (положить в банк) на n лет, чтобы при определённой доходности инвестиций (ставке процентов) i получит наращенную сумму, равную S. Для решения этой задачи используется формула 1.1:

PV=FV/(1+k)ⁿ или PV= FV (1+k)^-n (2.1)

где (1+n)^-n – дисконтный множитель, показывающий во сколько раз первоначальная сумма меньше наращенной (прил.2).

Пример 4. Через 1 год владелец векселя, выданного коммерческим банком, должен получить по нему 10 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составлять 25% годовых? По формуле (2.1) получим:

PV=10 / (1+0,25)¹ =8,0 тыс. руб.

ТЕМА 2. АНАЛИЗ ФИНАНСОВЫХ ИНВЕСТИЦИЙ

(ЗАДАЧА 2)