И учетных операций с учетом удержания комиссионных

Доходы от ссудных и учетных операций могут иметь форму суммы начисленных процентов или дисконта при покупке векселя. В этих операциях условиями контракта может быть предусмотрено удержание комиссионных, что приводит к росту эффективности операций учета векселя или кредитной сделки. Для оценки эффективности используется годовая ставка простых или сложных процентов, которая получила название эффективной процентной ставки, которую будем обозначить i_эф.

Ссудные операции

При выдаче кредита банк может удерживать комиссионные с суммы кредита S(0). Обозначим G – размер комиссионных, g – ставка комиссионных. Тогда G = S(0)g. Наращение по ставке i_эф величины (S(0) – G) дает наращенную сумму S(T) = S(0) (1+iT), если i_эф – ставка простых процентов:

(S(0) – G) (1+ i_эф Т) = S(T)

S(0) (1-g) (1+ i_эф Т) =S(0) (1+iT).

Сделав преобразование получаем формулу для эффективной ставки простых процентов:

i_эф = .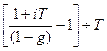

Если доходность измеряется в виде эффективной ставки сложных процентов, то соответствующая формула имеет вид:

i_эф.сл. = .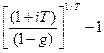

Пример 29.

Кредит выдан на 180 дней по ставке 80% годовых с удержанием комиссионных 2% от его суммы. Определить доходность кредитной операции с учетом удержания комиссионных при расчетном количестве дней в году 360.

Решение.

Доходность по простой ставке рассчитывается

i_эф = %.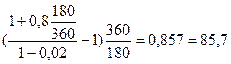

Доходность по сложной процентной ставке равна:

i_эф.сл. = %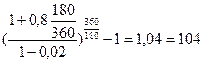

Заметим, что ставки 85,7% и 104% являются эквивалентными и показывают равную доходность финансовой операции.

Если бы банк не удерживал комиссионные, то эффективность была равна 80% годовых.

Учетные операции

При учете векселя комиссионные удерживаются с величины S(T), то есть сумма комиссионных равнаG=S(T)g. Балансовое уравнение для вывода формулы эффективной ставки простых процентов имеет вид:

(S(0)-G) (1+ i_эфT) = S(T)

Учитывая, что S(0) = S(T) (1-dT), величину (S(0)-G) определим как S(T) (1-dT-g). Тогда балансовое уравнение имеет вид:

S(T) (1-dT-g) (1+ i_эфT) = S(T)

Откуда получаем формулу для i_эф:

i_эф = .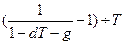

Если доходность измеряется по сложной ставке, то

i_эф.сл. = .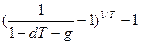

Доходность операций с ценными бумагами

При покупке ценных бумаг возможно получение дополнительного дохода или сохранение капитала от обесценения в условиях инфляции.

Расчет дохода по различным видам ценных бумаг производится на основе формул наращения и дисконтирования по процентной ставке. (Формулы приведены в соответствующих таблицах Справочника ЭУМК).

Рассмотрим следующие примеры.

Пример 30.

Депозитный сертификат номиналом 100 000 руб. выдан 14 мая на полгода с начислением по нему процентов по ставке 18 % годовых. Определить сумму дохода и сумму погашения долгового обязательства.

Решение:

Если начисляются точные проценты, то К = 365 и при использовании английской схемы начисления простых процентов точное число дней можно определить по специальной таблице. (См. таблицу определения порядковых дней в году в Справочнике ЭУМК). Оно составляет 184 дня.

Если используется германская схема начисления процентов, то срок составляет 6 × 30 = 180 дней.

На основе формул наращения по простой процентной ставке, приведенной в Справочнике ЭУМК, рассчитаем доход на сумму долга.

Для английской схемы:

I = 100000 × 0,18 × 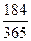= 9074 (руб.)

S(T) = 100000 + 9074 = 109074 (руб.)

Для германской схемы:

I = 100000 × 0,18 × 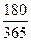= 9000 (руб.)

S(T) = 100000 + 9000 = 109000 (руб.)

Пример 31.

Платежное обязательство выдано на пять месяцев под 20 % годовых с погашением 200000 руб. Определить доход владельца данного платежного обязательства.

Решение:

По формуле дисконтирования рассчитаем современную стоимость обязательства:

S(o) = 200000 / (1 + 0,2 × 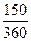)= 184672 (руб.)

I = 200000 – 184672 = 15328 (руб.)

Пример 32.

Сертификат номинальной стоимостью 150000 руб. выдан на 200 дней (К = 365) с погашением 180000 руб. Определить доходность сертификата в виде простой ставки ссудного процента.

Решение:

Определим процентную ставку i из уравнения:

180000 = 150000 (1 + i × )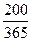

i = (180000 / 150000 – 1) ×365 / 200 = 36,5%