Стандартное отклонение для коэффициента регрессии Sb и t-статистика
Значения стандартного отклонения для коэффициентов регрессии Sb и значение статистики тесно взаимосвязаны. Sb рассчитываются как

Или в сокращенной форме:
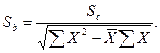
Sb задает интервал, в который попадают. Все возможные значения коэффициента регрессии. t-статистика (или t-значение) – мера статистической значимости влияния независимой переменной Х на зависимую переменную Y определяется путем деления оценки коэффициента b на его стандартное отклонение Sb. Полученное значение затем сравнивается с табличным (см. табл. В Приложении II).
Таким образом, t-статистика показывает, насколько велики величина стандартного отклонения для коэффициента регрессии (насколько оно больше нуля). Практика показывает, что любое t-значение, не принадлежащее интервалу [-2;2], является приемлемым. Чем выше t-значение, тем выше достоверность коэффициента (т.е. точнее прогноз на его основе). Низкое t-значение свидетельствует о низкой прогнозирующей силе коэффициента регрессии.
Вариант 7. Sb для нашего примера равно:
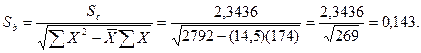
t-статистика определяется:
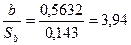
Так как t=3,94>2, можно заключить, что коэффициент b является статистически значимым. Как отмечалось раньше, табличное критическое значение (уровень отсечения) для 10 степеней свободы равно 2,228 (см. табл. в Приложении 11).
Обратите внимание:
- t-значения играют большую роль для коэффициентов множественной регрессии (множественная модель описывается с помощью нескольких коэффициентов b);
- R2 характеризует общее согласие (всего «леса» невязок на диаграмме разброса), в то время как t-значение характеризует отдельную независимую переменную (отдельное «дерево» невязок).
В общем случае табличное t-значение для заданных числа степеней свободы и уровня значимости используется, чтобы:
- установить диапазон предсказания: верхнюю и нижнюю границы для прогнозируемого значения при заданном значении независимой переменной;
-установить доверительные интервалы для коэффициентов регрессии;
- определить уровень отсечения для t-теста.
